7.12.2 The Restricted Active Space (RAS) Scheme

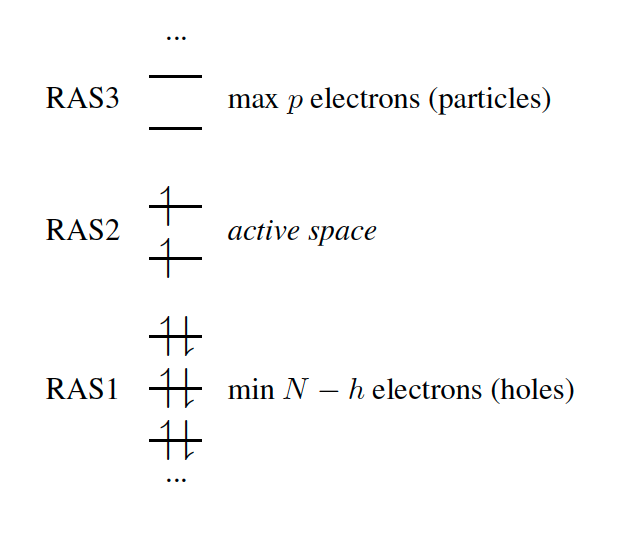
In the RAS formalism, we divide the orbital space into three subspaces called RAS1, RAS2 and RAS3 (Fig. 7.2). The RAS-CI states are defined by the number of orbitals and the restrictions in each subspace.

The single reference RAS-CI electronic wave functions are obtained by applying a spin-flipping or excitation operator $\widehat{R}$ on the reference determinant ${\varphi }^{\text{(0)}}$.

The $\widehat{R}$ operator must obey the restrictions imposed in the subspaces RAS1, RAS2 and RAS3, and can be decomposed as:

where ${\widehat{r}}^{\text{RAS2}}$ contains all possible electronic promotions within the RAS2 space, that is, a reduced full CI, and the rest of the terms generate configurations with different number of holes ($h$ super-index) in RAS1 and electrons in RAS3 ($p$ super-index). The current implementation truncates this series up to the inclusion of hole and particle contributions, i.e. the first three terms on the right hand side of Eq. (7.110).