7.12 Restricted Active Space Spin-Flip (RAS-SF) and Configuration Interaction (RAS-CI)7.12.1 Introduction 7.12.3 Second-Order Perturbative Corrections to RAS-CI

7.12.2 The Restricted Active Space (RAS) Scheme

(November 19, 2024)

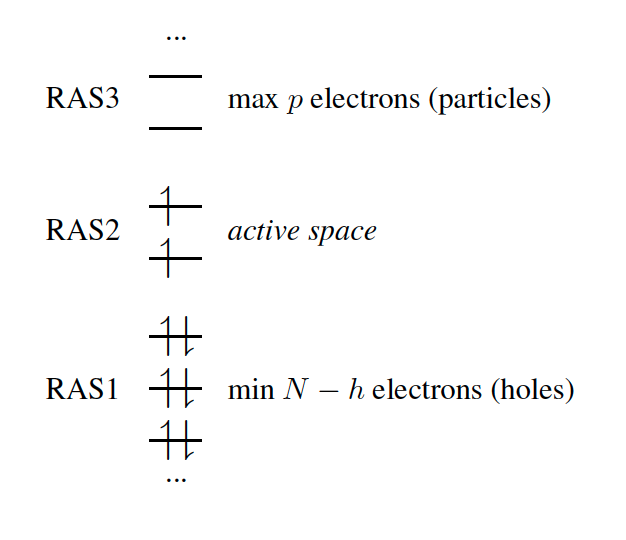
In the RAS formalism, one divides the orbital space into three subspaces called RAS1, RAS2 and RAS3 (Fig. 7.2). The RAS-CI states are defined by the number of orbitals and the restrictions in each subspace.

Figure 7.2: Orbital subspaces in RAS-CI employing a ROHF triplet reference.

The single reference RAS-CI electronic wave functions are obtained by applying a spin-flipping or excitation operator $\hat{R}$ on the reference determinant $|\phi^{\text{(0)}}\rangle$ .

$\left|{\Psi}^{\text{RAS}}\right>=\hat{R}\left|\phi^{\text{(0)}}\right>$

(7.137)

The $\hat{R}$ operator must obey the restrictions imposed in the subspaces RAS1, RAS2 and RAS3, and can be decomposed as:

$\hat{R}=\hat{r}^{\text{RAS2}}+\hat{r}^{h}+\hat{r}^{p}+\hat{r}^{hp}+\hat{r}^{2h% }+\hat{r}^{2p}+...$

(7.138)

where $\hat{r}^{\text{RAS2}}$ contains all possible electronic promotions within the RAS2 space, that is, a reduced full CI, and the rest of the terms generate configurations with different number of holes ( $h$ super-index) in RAS1 and electrons in RAS3 ( $p$ super-index). The current implementation truncates this series up to the inclusion of hole and particle contributions, i.e., the first three terms on the right hand side of Eq. (7.138).

Search Results

7.12.2 The Restricted Active Space (RAS) Scheme