Q-Chem 5.1 User’s Manual

13.10 The Explicit Polarization (XPol) Method

13.10.1 Theory

XPol is an approximate, fragment-based molecular orbital method that was developed as a “next-generation” force field.[Gao(1998), Xie and Gao(2007), Xie et al.(2008)Xie, Song, Truhlar, and Gao, Xie et al.(2009)Xie, Orozco, Truhlar, and Gao] The basic idea of the method is to treat a molecular liquid, solid, or cluster as a collection of fragments, where each fragment is a molecule. Intra-molecular interactions are treated with a self-consistent field method (Hartree-Fock or DFT), but each fragment is embedded in a field of point charges that represent electrostatic interactions with the other fragments. These charges are updated self-consistently by collapsing each fragment’s electron density onto a set of atom-centered point charges, using charge analysis procedures (Mulliken, Löwdin, or ChElPG, for example; see Section 11.2.1). This approach incorporates many-body polarization, at a cost that scales linearly with the number of fragments, but neglects the anti-symmetry requirement of the total electronic wave function. As a result, intermolecular exchange-repulsion is neglected, as is dispersion since the latter is an electron correlation effect. As such, the XPol treatment of polarization must be augmented with empirical, Lennard–Jones-type intermolecular potentials in order to obtain meaningful optimized geometries, vibrational frequencies or dynamics.

The XPol method is based upon an ansatz in which the super-system wave function is written as a direct product of fragment wave functions,

  \begin{equation} \label{eq:hartree_ pdt} |\Psi \rangle = \prod _ A^{N_\ensuremath{\mathrm{}}{frag}} | \Psi _{\! A} \rangle , \end{equation}   (13.17)

where $N_\ensuremath{\mathrm{}}{frag}$ is the number of fragments. We assume here that the fragments are molecules and that covalent bonds remain intact. The fragment wave functions are anti-symmetric with respect to exchange of electrons within a fragment, but not to exchange between fragments. For closed-shell fragments described by Hartree-Fock theory, the XPol total energy is[Xie et al.(2008)Xie, Song, Truhlar, and Gao, Jacobson and Herbert(2011)]

  \begin{equation} \label{eq:E_ xpol} E_{\rm XPol} = \sum _ A \left[ 2 \sum _{a} \mathbf{c}_ a^\dagger \left( \mathbf{h}^ A+ \mathbf{J}^ A - \tfrac {1}{2}\mathbf{K}^ A \right) \mathbf{c}_ a^{} +E_\ensuremath{\mathrm{}}{nuc}^ A \right] + E_\ensuremath{\mathrm{}}{embed} . \end{equation}   (13.18)

The term in square brackets is the ordinary Hartree-Fock energy expression for fragment $A$. Thus, $\mathbf{c}_ a^{}$ is a vector of occupied MO expansion coefficients (in the AO basis) for the occupied MO $a\in A$; $\mathbf{h}^ A$ consists of the one-electron integrals; and $\mathbf{J}^ A$ and $\mathbf{K}^ A$ are the Coulomb and exchange matrices, respectively, constructed from the density matrix for fragment $A$. The additional terms in Eq. eq:E_xpol,

  \begin{equation} \label{eq:E_ QMMM} E_\ensuremath{\mathrm{}}{embed} = \tfrac {1}{2} \sum _ A \sum _{B\neq A} \sum _{J\in B} \left( -2 \sum _ a \mathbf{c}_ a^\dagger \mathbf{I}_ J \mathbf{c}_ a + \sum _{I \in A} L_{IJ} \right) q_ J^{} , \end{equation}   (13.19)

arise from the electrostatic embedding. The matrix $\mathbf{I}_ J$ is defined by its AO matrix elements,

  \begin{equation} \label{eq:I} \left( \mathbf{I}_ J \right)_{\mu \nu } = \left\langle \mu \left| \frac{1}{\bigl |\vec{r}-\vec{R}_ J \bigr |} \right| \nu \right\rangle , \end{equation}   (13.20)

and $L_{IJ}$ is given by

  \begin{equation} \label{eq:L} L_{IJ} = \frac{Z_ I}{\bigl |\vec{R}_ I-\vec{R}_ J\bigr |} . \end{equation}   (13.21)

According to Eqs. eq:E_xpol and eq:E_QMMM, each fragment is embedded in the electrostatic potential arising from a set of point charges, $\{ q_ J^{}\} $, on all of the other fragments; the factor of $1/2$ in Eq. eq:E_QMMM avoids double-counting. Exchange interactions between fragments are ignored, and the electrostatic interactions between fragments are approximated by interactions between the charge density of one fragment and point charges on the other fragments.

Crucially, the vectors $\mathbf{c}_ a$ are constructed within the ALMO ansatz,[Khaliullin et al.(2006)Khaliullin, Head-Gordon, and Bell] so that MOs for each fragment are represented in terms of only those AOs that are centered on atoms in the same fragment. This choice affords a method whose cost grows linearly with respect to $N_\ensuremath{\mathrm{}}{frag}$, and where basis set superposition error is excluded by construction. In compact basis sets, the ALMO ansatz excludes inter- fragment charge transfer as well.

The original XPol method of Xie et al.[Xie and Gao(2007), Xie et al.(2008)Xie, Song, Truhlar, and Gao, Xie et al.(2009)Xie, Orozco, Truhlar, and Gao] uses Mulliken charges for the embedding charges $q_ J^{}$ in Eq. eq:E_QMMM, though other charge schemes could be envisaged. In non-minimal basis sets, the use of Mulliken charges is beset by severe convergence problems,[Jacobson and Herbert(2011)] and Q-Chem’s implementation of XPol offers the alternative of using either Löwdin charges or ChElPG charges,[Breneman and Wiberg(1990)] the latter being derived from the electrostatic potential as discussed in Section 11.2.1. The ChElPG charges are found to be stable and robust, albeit with a somewhat larger computational cost as compared to Mulliken or Löwdin charges.[Jacobson and Herbert(2011), Herbert et al.(2012)Herbert, Jacobson, Lao, and Rohrdanz] An algorithm to compute ChElPG charges using atom-centered Lebedev grids rather than traditional Cartesian grids is available (see Section 11.2.1),[Holden et al.(2013)Holden, Richard, and Herbert] which uses far fewer grid points and thus can significantly improve the performance for the XPol/ChElPG method, where these charges must be iteratively updated.

Researchers who use Q-Chem’s XPol code are asked to cite Refs. Jacobson:2011, and Herbert:2012.

13.10.2 Supplementing XPol with Empirical Potentials

In order to obtain physical results, one must either supplement the XPol energy expression with either empirical intermolecular potentials or else with an ab initio treatment of intermolecular interactions. The latter approach is described in Section 13.12. Here, we describe how to add Lennard-Jones or Buckingham potentials to the XPol energy, using the $xpol_mm and $xpol_params sections described below.

The Lennard-Jones potential is

  \begin{equation} \label{eq:Lennard-Jones} V_{\rm LJ}^{}(R_{ij}) = 4 \epsilon ^{}_{ij} \left[ \left(\frac{\sigma ^{}_{ij}}{R_{ij}}\right)^{\! 12} - \left(\frac{\sigma ^{}_{ij}}{R_{ij}}\right)^{\! 6} \right] \; , \end{equation}   (13.22)

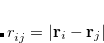where $R_{ij}$ represents the distance between atoms $i$ and $j$. This potential is characterized by two parameters, a well depth $\epsilon ^{}_{ij}$ and a length scale $\sigma ^{}_{ij}$. Although quite common, the $R^{-12}$ repulsion is unrealistically steep. The Buckingham potential replaces this with an exponential function,

  \begin{equation} \label{eq:Buckingham} V_{\rm Buck}^{}(R_{ij}) = \epsilon ^{}_{ij} \left[ A e^{-B \frac{R_{ij}}{\sigma ^{}_{ij}}} - C \left(\frac{\sigma ^{}_{ij}}{R_{ij}}\right)^{\! 6} \right] \; , \end{equation}   (13.23)

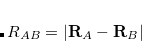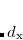Here, $A$, $B$, and $C$ are additional (dimensionless) constants, independent of atom type. In both Eq. eq:Lennard-Jones and Eq. eq:Buckingham, the parameters $\epsilon ^{}_{ij}$ and $\sigma _{ij}^{}$ are determined using the geometric mean of atomic well-depth and length-scale parameters. For example,

  \begin{equation} \sigma ^{}_{ij} = \sqrt {\sigma ^{}_ i \sigma _ j^{}} \; . \end{equation}   (13.24)

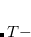The atomic parameters $\sigma _ i^{}$ and $\epsilon _ i^{}$ must be specified using a $xpol_mm section in the Q-Chem input file. The format is a molecular mechanics-like specification of atom types and connectivities. All atoms specified in the $molecule section must also be specified in the $xpol_mm section. Each line must contain an atom number, atomic symbol, Cartesian coordinates, integer atom type, and any connectivity data. The $xpol_params section specifies, for each atom type, a value for $\epsilon $ in kcal/mol and a value for 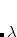$\sigma $ in Ångstroms. 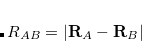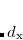A Lennard-Jones potential is used by default; if a Buckingham potential is desired, then the first line of the $xpol_params section should contain the string BUCKINGHAM followed by values for the $A$, $B$, and $C$ parameters.

13.10.3 Job Control Variables for XPol

XPol calculations are enabled by setting the $rem variable XPOL to TRUE. These calculations can be used in combination with Hartree-Fock theory and with most density functionals, a notable exception being that XPol is not yet implemented for meta-GGA functionals (Section 5.3). Combining XPol with solvation models (Section 12.2) or external charges ($external_charges) is also not available. Analytic gradients are available when Mulliken or Löwdin embedding charges are used, but not yet available for ChElPG embedding charges.

XPOL

Perform a self-consistent XPol calculation.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

TRUE

Perform an XPol calculation.

FALSE

Do not perform an XPol calculation.

RECOMMENDATION:

NONE


XPOL_CHARGE_TYPE

Controls the type of atom-centered embedding charges for XPol calculations.


TYPE:

STRING


DEFAULT:

QLOWDIN


OPTIONS:

QLOWDIN

Löwdin charges.

QMULLIKEN

Mulliken charges.

QCHELPG

ChElPG charges.


RECOMMENDATION:

Problems with Mulliken charges in extended basis sets can lead to XPol convergence failure. Löwdin charges tend to be more stable, and ChElPG charges are both robust and provide an accurate electrostatic embedding. However, ChElPG charges are more expensive to compute, and analytic energy gradients are not yet available for this choice.


XPOL_MPOL_ORDER

Controls the order of multipole expansion that describes electrostatic interactions.


TYPE:

STRING


DEFAULT:

CHARGES


OPTIONS:

GAS

No electrostatic embedding; monomers are in the gas phase.

CHARGES

Charge embedding.

DENSITY

Density embedding.


RECOMMENDATION:

Should be set to GAS to do a dimer SAPT calculation (see Section 13.11).


XPOL_PRINT

Print level for XPol calculations.


TYPE:

INTEGER


DEFAULT:

1


OPTIONS:

$N$

Integer print level


RECOMMENDATION:

Higher values prints more information


XPOL_OMEGA

Controls the range-separation parameter, $\omega $, that is used in long-range-corrected DFT.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

TRUE

Use different $\omega $ values for different fragments.

FALSE

Use a single value of $\omega $ for all fragments.


RECOMMENDATION:

If FALSE, the $rem variable OMEGA should be used to specify the single value of $\omega $. If TRUE, separate values for each fragment should be specified in an $lrc_omega input section. Values in the $lrc_omega section have the same units as the $rem variable OMEGA, namely, $\omega = $ OMEGA/1000, in atomic units.


13.10.4 Examples

XPol on its own is not a useful method (as it neglects all intermolecular interactions except for polarization), so the two examples below demonstrate the use of XPol in conjunction with a Lennard-Jones and a Buckingham potential, respectively.

Example 13.329  An XPol single point calculation on the water dimer using a Lennard-Jones potential.

$molecule
0 1
-- water 1
0 1
O          -1.364553     .041159     .045709
H          -1.822645     .429753    -.713256
H          -1.841519    -.786474     .202107
-- water 2
0 1
O           1.540999     .024567     .107209
H            .566343     .040845     .096235
H           1.761811    -.542709    -.641786
$end

$rem
   METHOD           HF
   BASIS            3-21G
   XPOL             TRUE
   XPOL_CHARGE_TYPE QLOWDIN
$end

$xpol_mm
   1 O          -1.364553     .041159     .045709 1 2 3
   2 H          -1.822645     .429753    -.713256 2 1
   3 H          -1.841519    -.786474     .202107 2 1
   4 O           1.540999     .024567     .107209 1 5 6
   5 H            .566343     .040845     .096235 2 4
   6 H           1.761811    -.542709    -.641786 2 4
$end

$xpol_params
   1            0.16     3.16
   2            0.00     0.00
$end


Example 13.330  An XPol single point calculation on the water dimer using a Buckingham potential.

$molecule
0 1
-- water 1
0 1
O          -1.364553     .041159     .045709
H          -1.822645     .429753    -.713256
H          -1.841519    -.786474     .202107
-- water 2
0 1
O           1.540999     .024567     .107209
H            .566343     .040845     .096235
H           1.761811    -.542709    -.641786
$end

$rem
   METHOD           HF
   BASIS            3-21G
   XPOL             TRUE
   XPOL_CHARGE_TYPE QLOWDIN
$end

$xpol_mm
   1 O          -1.364553     .041159     .045709 1 2 3
   2 H          -1.822645     .429753    -.713256 2 1
   3 H          -1.841519    -.786474     .202107 2 1
   4 O           1.540999     .024567     .107209 1 5 6
   5 H            .566343     .040845     .096235 2 4
   6 H           1.761811    -.542709    -.641786 2 4
$end

$xpol_params
   BUCKINGHAM   500000.0 12.5 2.25
   1            0.16     3.16
   2            0.00     0.00
$end