5.3 Overview of Available Functionals
Q-Chem currently has more than 30 exchange functionals as well as more than 30 correlation functionals, and in addition over 150 exchange-correlation (XC) functionals, which refer to functionals that are not separated into exchange and correlation parts, either because the way in which they were parameterized renders such a separation meaningless (e.g., B97-D[Grimme(2006b)] or  B97X[Chai and Head-Gordon(2008a)]) or because they are a standard linear combination of exchange and correlation (e.g., PBE[Perdew et al.(1996)Perdew, Burke, and Ernzerhof] or B3LYP[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch]). User-defined XC functionals can be created as specified linear combinations of any of the 30+ exchange functionals and/or the 30+ correlation functionals.
B97X[Chai and Head-Gordon(2008a)]) or because they are a standard linear combination of exchange and correlation (e.g., PBE[Perdew et al.(1996)Perdew, Burke, and Ernzerhof] or B3LYP[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch]). User-defined XC functionals can be created as specified linear combinations of any of the 30+ exchange functionals and/or the 30+ correlation functionals.
KS-DFT functionals can be organized onto a ladder with five rungs, in a classification scheme (“Jacob’s Ladder”) proposed by John Perdew[Perdew et al.(2005)Perdew, Ruzsinszky, Tao, Staroverov, Scuseria, and Csonka] in 2001. The first rung contains a functional that only depends on the (spin-)density 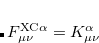 , namely, the local spin-density approximation (LSDA). These functionals are exact for the infinite uniform electron gas (UEG), but are highly inaccurate for molecular properties whose densities exhibit significant inhomogeneity. To improve upon the weaknesses of the LSDA, it is necessary to introduce an ingredient that can account for inhomogeneities in the density: the density gradient,
, namely, the local spin-density approximation (LSDA). These functionals are exact for the infinite uniform electron gas (UEG), but are highly inaccurate for molecular properties whose densities exhibit significant inhomogeneity. To improve upon the weaknesses of the LSDA, it is necessary to introduce an ingredient that can account for inhomogeneities in the density: the density gradient, 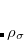 . These generalized gradient approximation (GGA) functionals define the second rung of Jacob’s Ladder and tend to improve significantly upon the LSDA. Two additional ingredients that can be used to further improve the performance of GGA functionals are either the Laplacian of the density
. These generalized gradient approximation (GGA) functionals define the second rung of Jacob’s Ladder and tend to improve significantly upon the LSDA. Two additional ingredients that can be used to further improve the performance of GGA functionals are either the Laplacian of the density 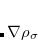 , and/or the kinetic energy density,
, and/or the kinetic energy density,
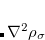 |
(5.17) |
While functionals that employ both of these options are available in Q-Chem, the kinetic energy density is by far the more popular ingredient and has been used in many modern functionals to add flexibility to the functional form with respect to both constraint satisfaction (non-empirical functionals) and least-squares fitting (semi-empirical parameterization). Functionals that depend on either of these two ingredients belong to the third rung of the Jacob’s Ladder and are called meta-GGAs. These meta-GGAs often further improve upon GGAs in areas such as thermochemistry, kinetics (reaction barrier heights), and even non-covalent interactions.
Functionals on the fourth rung of Jacob’s Ladder are called hybrid density functionals. This rung contains arguably the most popular density functional of our time, B3LYP, the first functional to see widespread application in chemistry. “Global” hybrid (GH) functionals such as B3LYP (as distinguished from the “range-separated hybrids" introduced below) add a constant fraction of “exact” (Hartree-Fock) exchange to any of the functionals from the first three rungs. Thus, hybrid LSDA, hybrid GGA, and hybrid meta-GGA functionals can be constructed, although the latter two types are much more common. As an example, the formula for the B3LYP functional, as implemented in Q-Chem, is
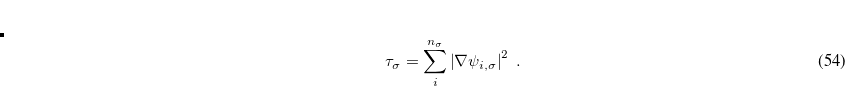 |
(5.18) |
where 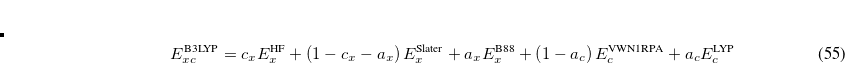 ,
, 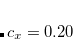 , and
, and 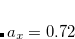 .
.
A more recent approach to introducing exact exchange into the functional form is via range separation. Range-separated hybrid (RSH) functionals split the exact exchange contribution into a short-range (SR) component and a long-range (LR) component, often by means of the error function (erf) and complementary error function (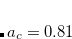 ):
):
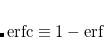 |
(5.19) |
The first term on the right in Eq. () is singular but short-range, and decays to zero on a length scale of 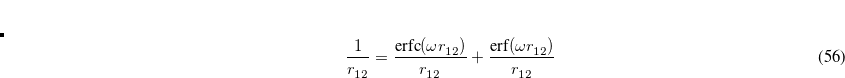 , while the second term constitutes a non-singular, long-range background. An RSH XC functional can be expressed generically as
, while the second term constitutes a non-singular, long-range background. An RSH XC functional can be expressed generically as
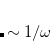 |
(5.20) |
where the SR and LR parts of the Coulomb operator are used, respectively, to evaluate the HF exchange energies 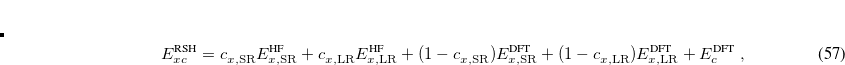 and
and 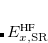 . The corresponding DFT exchange functional is partitioned in the same manner, but the correlation energy
. The corresponding DFT exchange functional is partitioned in the same manner, but the correlation energy 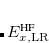 is evaluated using the full Coulomb operator,
is evaluated using the full Coulomb operator, 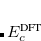 . Of the two linear parameters in Eq. eq:RSHGGA,
. Of the two linear parameters in Eq. eq:RSHGGA, 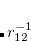 is usually either set to 1 to define long-range corrected (LRC) RSH functionals (see Section 5.6) or else set to 0, which defines screened-exchange (SE) RSH functionals. On the other hand, the fraction of short-range exact exchange (
is usually either set to 1 to define long-range corrected (LRC) RSH functionals (see Section 5.6) or else set to 0, which defines screened-exchange (SE) RSH functionals. On the other hand, the fraction of short-range exact exchange (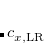 ) can either be determined via least-squares fitting, theoretically justified using the adiabatic connection, or simply set to zero. As with the global hybrids, RSH functionals can be fashioned using all of the ingredients from the lower three rungs. The rate at which the local DFT exchange is turned off and the non-local exact exchange is turned on is controlled by the parameter
) can either be determined via least-squares fitting, theoretically justified using the adiabatic connection, or simply set to zero. As with the global hybrids, RSH functionals can be fashioned using all of the ingredients from the lower three rungs. The rate at which the local DFT exchange is turned off and the non-local exact exchange is turned on is controlled by the parameter  . Large values of
. Large values of  tend to lead to attenuators that are less smooth (unless the fraction of short-range exact exchange is very large), while small values of (e.g.,
tend to lead to attenuators that are less smooth (unless the fraction of short-range exact exchange is very large), while small values of (e.g., 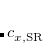 0.2–0.3 bohr
0.2–0.3 bohr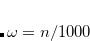 ) are the most common in semi-empirical RSH functionals.
) are the most common in semi-empirical RSH functionals.
The final rung on Jacob’s Ladder contains functionals that use not only occupied orbitals (via exact exchange), but virtual orbitals as well (via methods such as MP2 or the random phase approximation, RPA). These double hybrids (DH) are the most expensive density functionals available in Q-Chem, but can also be very accurate. The most basic form of a DH functional is
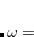 |
(5.21) |
As with hybrids, the coefficients can either be theoretically motivated or empirically determined. In addition, double hybrids can use exact exchange both globally or via range-separation, and their components can be as primitive as LSDA or as advanced as in meta-GGA functionals. More information on double hybrids can be found in Section 5.9.
Finally, the last major advance in KS-DFT in recent years has been the development of methods that are capable of accurately describing non-covalent interactions, particularly dispersion. All of the functionals from Jacob’s Ladder can technically be combined with these dispersion corrections, although in some cases the combination is detrimental, particularly for semi-empirical functionals that were parameterized in part using data sets of non-covalent interactions, and already tend to overestimate non-covalent interaction energies. The most popular such methods available in Q-Chem are:
Non-local correlation (NLC) functionals (Section 5.7.1), including those of Vydrov and Van Voorhis[Vydrov and Van Voorhis(2009), Vydrov and Van Voorhis(2010b)] (VV09 and VV10) and of Lundqvist and Langreth[Dion et al.(2004)Dion, Rydberg, Schröder, Langreth, and Lundqvist, Dion et al.(2005)Dion, Rydberg, Schröder, Langreth, and Lundqvist] (vdW-DF-04 and vdW-DF-10). The revised VV10 NLC functional of Sabatini and coworkers (rVV10) is also available[Sabatini et al.(2013)Sabatini, Gorni, and de Gironcoli].
Damped, atom–atom pairwise empirical dispersion potentials from Grimme and others[Grimme(2006b), Chai and Head-Gordon(2008b), Grimme et al.(2010)Grimme, Antony, Ehrlich, and Krieg, Grimme et al.(2011)Grimme, Ehrlich, and Goerigk, Schröder et al.(2015)Schröder, Creon, and Schwabe, Smith et al.(2016)Smith, Burns, Patkowski, and Sherrill] [DFT-D2, DFT-CHG, DFT-D3(0), DFT-D3(BJ), DFT-D3(CSO), DFT-D3M(0), DFT-D3M(BJ), and DFT-D3(op)]; see Section 5.7.2.
The exchange-dipole models (XDM) of Johnson and Becke (XDM6 and XDM10); see Section 5.7.3.
The Tkatchenko and Scheffler (TS) method for dispersion interactions[Tkatchenko and Scheffler(2009)]; see Section 5.7.4.
The Many-Body Dispersion (MBD) method for van der Waals interactions[Tkatchenko et al.(2012)Tkatchenko, DiStasio, Jr., Car, and Scheffler, Ambrosetti et al.(2014)Ambrosetti, Reilly, DiStasio, Jr., and Tkatchenko]; see Section 5.7.5.
Below, we categorize the functionals that are available in Q-Chem, including exchange functionals (Section 5.3.2), correlation functionals (Section 5.3.3), and exchange-correlation functionals (Section 5.3.4). Within each category the functionals will be categorized according to Jacob’s Ladder. Exchange and correlation functionals can be invoked using the $rem variables EXCHANGE and CORRELATION, while the exchange-correlation functionals can be invoked either by setting the $rem variable METHOD or alternatively (in most cases, and for backwards compatibility with earlier versions of Q-Chem) by using the $rem variable EXCHANGE. Some caution is warranted here. While setting METHOD to PBE, for example, requests the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional,[Perdew et al.(1996)Perdew, Burke, and Ernzerhof] which includes both PBE exchange and PBE correlation, setting EXCHANGE = PBE requests only the exchange component and setting CORRELATION = PBE requests only the correlation component. Setting both of these values is equivalent to specifying METHOD = PBE.
Single-Point |
Optimization |
Frequency |
|
Ground State |
LSDA |
LSDA |
LSDA |
GGA |
GGA |
GGA |
|
meta-GGA |
meta-GGA |
— |
|
GH |
GH |
GH |
|
RSH |
RSH |
RSH |
|
NLC |
NLC |
— |
|
DFT-D |
DFT-D |
DFT-D |
|
XDM |
— |
— |
|
TDDFT |
LSDA |
LSDA |
LSDA |
GGA |
GGA |
GGA |
|
meta-GGA |
— |
— |
|
GH |
GH |
GH |
|
RSH |
RSH |
— |
|
— |
— |
— |
|
DFT-D |
DFT-D |
DFT-D |
|
— |
— |
— |
|
|
|||
|
|||
Finally, Table 5.1 provides a summary, arranged according to Jacob’s Ladder, of which categories of functionals are available with analytic first derivatives (for geometry optimizations) or second derivatives (for vibrational frequency calculations). If analytic derivatives are not available for the requested job type, Q-Chem will automatically generate them via finite difference. Tests of the finite-difference procedure, in cases where analytic second derivatives are available, suggest that finite-difference frequencies are accurate to  cm
cm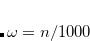 , except for very low-frequency, non-bonded modes.[Liu et al.(2017)Liu, Liu, and Herbert] Also listed in Table 5.1 are which functionals are available for excited-state time-dependent DFT (TDDFT) calculations, as described in Section 7.3. Lastly, Table 5.1 describes which functionals have been parallelized with OpenMP and/or MPI.
, except for very low-frequency, non-bonded modes.[Liu et al.(2017)Liu, Liu, and Herbert] Also listed in Table 5.1 are which functionals are available for excited-state time-dependent DFT (TDDFT) calculations, as described in Section 7.3. Lastly, Table 5.1 describes which functionals have been parallelized with OpenMP and/or MPI.
5.3.1 Suggested Density Functionals
Q-Chem contains over 150 exchange-correlation functionals, not counting those that can be straightforwardly appended with a dispersion correction (such as B3LYP-D3). Therefore, we suggest a few functionals from the second through fourth rungs of Jacob’s Ladder in order to guide functional selection. Most of these suggestions come from a benchmark of over 200 density functionals on a vast database of nearly 5000 data points, covering non-covalent interactions, isomerization energies, thermochemistry, and barrier heights. The single recommended method from each category is indicated in bold.
From the GGAs on Rung 2, we recommend:
B97-D3(BJ) – METHOD B97-D3 and DFT_D D3_BJ
revPBE-D3(BJ) – METHOD revPBE and DFT_D D3_BJ
BLYP-D3(BJ) – METHOD BLYP and DFT_D D3_BJ
PBE – METHOD PBE
From the meta-GGAs on Rung 3, we recommend:
B97M-rV – METHOD B97M-rV
MS1-D3(0) – METHOD MS1 and DFT_D D3_ZERO
MS2-D3(0) – METHOD MS2 and DFT_D D3_ZERO
M06-L-D3(0) – METHOD M06-L and DFT_D D3_ZERO
TPSS-D3(BJ) – METHOD TPSS and DFT_D D3_BJ
From the hybrid GGAs on Rung 4, we recommend:
 B97X-V – METHOD wB97X-V
B97X-V – METHOD wB97X-V  B97X-D3 – METHOD wB97X-D3
B97X-D3 – METHOD wB97X-D3  B97X-D – METHOD wB97X-D
B97X-D – METHOD wB97X-D B3LYP-D3(BJ) – METHOD B3LYP and DFT_D D3_BJ
revPBE0-D3(BJ) – METHOD revPBE0 and DFT_D D3_BJ
From the hybrid meta-GGAs on Rung 4, we recommend:
 B97M-V – METHOD wB97M-V
B97M-V – METHOD wB97M-V  M05-D – METHOD wM05-D
M05-D – METHOD wM05-D M06-2X-D3(0) – METHOD M06-2X and DFT_D D3_ZERO
TPSSh-D3(BJ) – METHOD TPSSh and DFT_D D3_BJ
5.3.2 Exchange Functionals
Note: All exchange functionals in this section can be invoked using the $rem variable EXCHANGE. Popular and/or recommended functionals within each class are listed first and indicated in bold. The rest are in alphabetical order.
Local Spin-Density Approximation (LSDA)
Slater – Slater-Dirac exchange functional (X
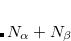 method with
method with 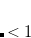 )[Dirac(1930)]
)[Dirac(1930)] SR_LSDA (BNL) – Short-range version of the Slater-Dirac exchange functional[Gill et al.(1996)Gill, Adamson, and Pople]
Generalized Gradient Approximation (GGA)
PBE – Perdew, Burke, and Ernzerhof exchange functional[Perdew et al.(1996)Perdew, Burke, and Ernzerhof]
B88 – Becke exchange functional from 1988[Becke(1988b)]
revPBE – Zhang and Yang one-parameter modification of the PBE exchange functional[Zhang and Yang(1998)]
AK13 – Armiento-Kümmel exchange functional from 2013[Armiento and Kümmel(2013)]
B86 – Becke exchange functional (X
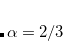 ) from 1986[Becke(1986a)]
) from 1986[Becke(1986a)] G96 – Gill exchange functional from 1996[Gill(1996)]
mB86 – Becke “modified gradient correction” exchange functional from 1986[Becke(1986b)]
mPW91 – modified version (Adamo and Barone) of the 1991 Perdew-Wang exchange functional[Adamo and Barone(1998)]
muB88 (
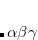 B88) – Short-range version of the B88 exchange functional by Hirao and coworkers[Iikura et al.(2001)Iikura, Tsuneda, Yanai, and Hirao]
B88) – Short-range version of the B88 exchange functional by Hirao and coworkers[Iikura et al.(2001)Iikura, Tsuneda, Yanai, and Hirao] muPBE (
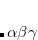 PBE) – Short-range version of the PBE exchange functional by Hirao and coworkers[Iikura et al.(2001)Iikura, Tsuneda, Yanai, and Hirao]
PBE) – Short-range version of the PBE exchange functional by Hirao and coworkers[Iikura et al.(2001)Iikura, Tsuneda, Yanai, and Hirao] optB88 – Refit version of the original B88 exchange functional (for use with vdW-DF-04) by Michaelides and coworkers[Klimeš et al.(2010)Klimeš, Bowler, and Michaelides]
OPTX – Two-parameter exchange functional by Handy and Cohen[Handy and Cohen(2001)]
PBEsol – PBE exchange functional modified for solids[Perdew et al.(2008a)Perdew, Ruzsinszky, Csonka, Vydrov, Scuseria, Constantin, Zhou, and Burke]
PW86 – Perdew-Wang exchange functional from 1986[Perdew and Wang(1986)]
PW91 – Perdew-Wang exchange functional from 1991[Perdew et al.(1992)Perdew, Chevary, Vosko, Jackson, Pederson, Singh, and Fiolhais]
RPBE – Hammer, Hansen, and Norskov exchange functional (modification of PBE)[Hammer et al.(1999)Hammer, Hansen, and Nørskov]
rPW86 – Revised version (Murray et al.) of the 1986 Perdew-Wang exchange functional[Murray et al.(2009)Murray, Lee, and Langreth]
SOGGA – Second-order GGA functional by Zhao and Truhlar[Zhao and Truhlar(2006c)]
wPBE (
 PBE) – Henderson et al. model for the PBE GGA short-range exchange hole[Henderson et al.(2008)Henderson, Janesko, and Scuseria]
PBE) – Henderson et al. model for the PBE GGA short-range exchange hole[Henderson et al.(2008)Henderson, Janesko, and Scuseria]
Meta-Generalized Gradient Approximation (meta-GGA)
TPSS – Tao, Perdew, Staroverov, and Scuseria exchange functional[Tao et al.(2003)Tao, Perdew, Staroverov, and Scuseria]
revTPSS – Revised version of the TPSS exchange functional[Perdew et al.(2009)Perdew, Ruzsinszky, Csonka, Constantin, and Sun]
BLOC – Minor modification of the TPSS exchange functional that works best with TPSSloc correlation (both by Della Sala and coworkers)[Constantin et al.(2013)Constantin, Fabiano, and Sala]
modTPSS – One-parameter version of the TPSS exchange functional[Perdew et al.(2007)Perdew, Ruzsinszky, Tao, Csonka, and Scuseria]
oTPSS – TPSS exchange functional with 5 refit parameters (for use with oTPSS correlation) by Grimme and coworkers[Goerigk and Grimme(2010)]
PBE-GX – First exchange functional based on a finite uniform electron gas (rather than an infinite UEG) by Pierre-François Loos[Loos(2017)]
PKZB – Perdew, Kurth, Zupan, and Blaha exchange functional[Perdew et al.(1999)Perdew, Kurth, Zupan, and Blaha]
regTPSS – Regularized (fixed order of limits issue) version of the TPSS exchange functional[Ruzsinszky et al.(2012)Ruzsinszky, Sun, Xiao, and Csonka]
SCAN – Strongly Constrained and Appropriately Normed exchange functional[Sun et al.(2015b)Sun, Ruzsinszky, and Perdew]
TM – Tao-Mo exchange functional derived via an accurate modeling of the conventional exchange hole[Tao and Mo(2016)]
5.3.3 Correlation Functionals
Note: All correlation functionals in this section can be invoked using the $rem variable CORRELATION. Popular and/or recommended functionals within each class are listed first and indicated in bold. The rest are in alphabetical order.
Local Spin-Density Approximation (LSDA)
PW92 – Perdew-Wang parameterization of the LSDA correlation energy from 1992[Perdew and Wang(1992)]
VWN5 (VWN) – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #5[Vosko et al.(1980)Vosko, Wilk, and Nusair]
Liu-Parr – Liu-Parr
 model from the functional expansion formulation[Liu and Parr(2000)]
model from the functional expansion formulation[Liu and Parr(2000)] PK09 – Proynov-Kong parameterization of the LSDA correlation energy from 2009[Proynov and Kong(2009)]
PW92RPA – Perdew-Wang parameterization of the LSDA correlation energy from 1992 with RPA values[Perdew and Wang(1992)]
PZ81 – Perdew-Zunger parameterization of the LSDA correlation energy from 1981[Perdew and Zunger(1981)]
VWN1 – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #1[Vosko et al.(1980)Vosko, Wilk, and Nusair]
VWN1RPA – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #1 with RPA values[Vosko et al.(1980)Vosko, Wilk, and Nusair]
VWN2 – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #2[Vosko et al.(1980)Vosko, Wilk, and Nusair]
VWN3 – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #3[Vosko et al.(1980)Vosko, Wilk, and Nusair]
VWN4 – Vosko-Wilk-Nusair parameterization of the LSDA correlation energy #4[Vosko et al.(1980)Vosko, Wilk, and Nusair]
Wigner – Wigner correlation functional (simplification of LYP)[Wigner(1938), Stewart and Gill(1995)]
Generalized Gradient Approximation (GGA)
PBE – Perdew, Burke, and Ernzerhof correlation functional[Perdew et al.(1996)Perdew, Burke, and Ernzerhof]
LYP – Lee-Yang-Parr opposite-spin correlation functional[Lee et al.(1988)Lee, Yang, and Parr]
P86 – Perdew-Wang correlation functional from 1986 based on the PZ81 LSDA functional[Perdew(1986)]
P86VWN5 – Perdew-Wang correlation functional from 1986 based on the VWN5 LSDA functional[Perdew(1986)]
PBEloc – PBE correlation functional with a modified beta term by Della Sala and coworkers[Constantin et al.(2012)Constantin, Fabiano, and Sala]
PBEsol – PBE correlation functional modified for solids[Perdew et al.(2008a)Perdew, Ruzsinszky, Csonka, Vydrov, Scuseria, Constantin, Zhou, and Burke]
PW91 – Perdew-Wang correlation functional from 1991[Perdew et al.(1992)Perdew, Chevary, Vosko, Jackson, Pederson, Singh, and Fiolhais]
regTPSS – Slight modification of the PBE correlation functional (also called vPBEc)[Ruzsinszky et al.(2012)Ruzsinszky, Sun, Xiao, and Csonka]
Meta-Generalized Gradient Approximation (meta-GGA)
TPSS – Tao, Perdew, Staroverov, and Scuseria correlation functional[Tao et al.(2003)Tao, Perdew, Staroverov, and Scuseria]
revTPSS – Revised version of the TPSS correlation functional[Perdew et al.(2009)Perdew, Ruzsinszky, Csonka, Constantin, and Sun]
B95 – Becke’s two-parameter correlation functional from 1995[Becke(1996)]
oTPSS – TPSS correlation functional with 2 refit parameters (for use with oTPSS exchange) by Grimme and coworkers[Goerigk and Grimme(2010)]
PK06 – Proynov-Kong “tLap” functional with
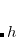 and Laplacian dependence[Proynov and Kong(2007)]
and Laplacian dependence[Proynov and Kong(2007)] PKZB – Perdew, Kurth, Zupan, and Blaha correlation functional[Perdew et al.(1999)Perdew, Kurth, Zupan, and Blaha]
SCAN – Strongly Constrained and Appropriately Normed correlation functional[Sun et al.(2015b)Sun, Ruzsinszky, and Perdew]
TM – Tao-Mo correlation functional, representing a minor modification to the TPSS correlation functional[Tao and Mo(2016)]
TPSSloc – The TPSS correlation functional with the PBE component replaced by the PBEloc correlation functional[Constantin et al.(2012)Constantin, Fabiano, and Sala]
5.3.4 Exchange-Correlation Functionals
Note: All exchange-correlation functionals in this section can be invoked using the $rem variable METHOD. For backwards compatibility, all of the exchange-correlation functionals except for the ones marked with an asterisk can be used with the $rem variable EXCHANGE. Popular and/or recommended functionals within each class are listed first and indicated in bold. The rest are in alphabetical order.
Local Spin-Density Approximation (LSDA)
SPW92* – Slater LSDA exchange + PW92 LSDA correlation
LDA – Slater LSDA exchange + VWN5 LSDA correlation
SVWN5* – Slater LSDA exchange + VWN5 LSDA correlation
Generalized Gradient Approximation (GGA)
B97-D3(0) – B97-D with a fitted DFT-D3(0) tail instead of the original DFT-D2 tail[Grimme et al.(2010)Grimme, Antony, Ehrlich, and Krieg]
B97-D – 9-parameter dispersion-corrected (DFT-D2) functional by Grimme[Grimme(2006b)]
PBE* – PBE GGA exchange + PBE GGA correlation
BLYP* – B88 GGA exchange + LYP GGA correlation
revPBE* – revPBE GGA exchange + PBE GGA correlation
BEEF-vdW – 31-parameter semi-empirical exchange functional developed via a Bayesian error estimation framework paired with PBE correlation and vdW-DF-10 NLC[Wellendorff et al.(2012)Wellendorff, Lundgaard, Møgelhøj, Petzold, Landis, Nørskov, Bligaard, and Jacobsen]
BOP – B88 GGA exchange + BOP “one-parameter progressive” GGA correlation[Tsuneda et al.(1999)Tsuneda, Suzumura, and Hirao]
BP86* – B88 GGA exchange + P86 GGA correlation
BP86VWN* – B88 GGA exchange + P86VWN5 GGA correlation
BPBE* – B88 GGA exchange + PBE GGA correlation
EDF1 – Modification of BLYP to give good performance in the 6-31+G* basis set[Adamson et al.(1998)Adamson, Gill, and Pople]
EDF2 – Modification of B3LYP to give good performance in the cc-pVTZ basis set for frequencies[Lin et al.(2004)Lin, George, and Gill]
GAM – 21-parameter non-separable gradient approximation functional by Truhlar and coworkers[Yu et al.(2015)Yu, Zhang, Verma, He, and Truhlar]
HCTH93 (HCTH/93) – 15-parameter functional trained on 93 systems by Handy and coworkers[Hamprecht et al.(1998)Hamprecht, Cohen, Tozer, and Handy]
HCTH120 (HCTH/120) – 15-parameter functional trained on 120 systems by Boese et al.[Boese et al.(2000)Boese, Doltsinis, Handy, and Sprik]
HCTH147 (HCTH/147) – 15-parameter functional trained on 147 systems by Boese et al.[Boese et al.(2000)Boese, Doltsinis, Handy, and Sprik]
HCTH407 (HCTH/407) – 15-parameter functional trained on 407 systems by Boese and Handy[Boese and Handy(2001)]
HLE16 – HCTH/407 exchange functional enhanced by a factor of 1.25 + HCTH/407 correlation functional enhanced by a factor of 0.5[Verma and Truhlar(2017)]
KT1 – GGA functional designed specifically for shielding constant calculations[Keal and Tozer(2003)]
KT2 – GGA functional designed specifically for shielding constant calculations[Keal and Tozer(2003)]
KT3 – GGA functional with improved results for main-group nuclear magnetic resonance shielding constants[Keal and Tozer(2004)]
mPW91* – mPW91 GGA exchange + PW91 GGA correlation
N12 – 21-parameter non-separable gradient approximation functional by Peverati and Truhlar[Peverati and Truhlar(2012b)]
OLYP* – OPTX GGA exchange + LYP GGA correlation
PBEOP – PBE GGA exchange + PBEOP “one-parameter progressive” GGA correlation[Tsuneda et al.(1999)Tsuneda, Suzumura, and Hirao]
PBEsol* – PBEsol GGA exchange + PBEsol GGA correlation
PW91* – PW91 GGA exchange + PW91 GGA correlation
RPBE* – RPBE GGA exchange + PBE GGA correlation
rVV10* – rPW86 GGA exchange + PBE GGA correlation + rVV10 non-local correlation[Sabatini et al.(2013)Sabatini, Gorni, and de Gironcoli]
SOGGA* – SOGGA GGA exchange + PBE GGA correlation
SOGGA11 – 20-parameter functional by Peverati, Zhao, and Truhlar[Peverati et al.(2011)Peverati, Zhao, and Truhlar]
VV10 – rPW86 GGA exchange + PBE GGA correlation + VV10 non-local correlation[Vydrov and Van Voorhis(2010b)]
Meta-Generalized Gradient Approximation (meta-GGA)
B97M-V – 12-parameter combinatorially-optimized, dispersion-corrected (VV10) functional by Mardirossian and Head-Gordon[Mardirossian and Head-Gordon(2015)]
B97M-rV* – B97M-V density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon]
M06-L – 34-parameter functional by Zhao and Truhlar[Zhao and Truhlar(2006a)]
TPSS* – TPSS meta-GGA exchange + TPSS meta-GGA correlation
revTPSS* – revTPSS meta-GGA exchange + revTPSS meta-GGA correlation
BLOC* – BLOC meta-GGA exchange + TPSSloc meta-GGA correlation
M11-L – 44-parameter dual-range functional by Peverati and Truhlar[Peverati and Truhlar(2012a)]
mBEEF – 64-parameter exchange functional paired with the PBEsol correlation functional[Wellendorff et al.(2014)Wellendorff, Lundgaard, Jacobsen, and Bligaard]
MGGA_MS0 – MGGA_MS0 meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2012)Sun, Xiao, and Ruzsinszky]
MGGA_MS1 – MGGA_MS1 meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2013)Sun, Haunschild, Xiao, Bulik, Scuseria, and Perdew]
MGGA_MS2 – MGGA_MS2 meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2013)Sun, Haunschild, Xiao, Bulik, Scuseria, and Perdew]
MGGA_MVS – MGGA_MVS meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2015a)Sun, Perdew, and Ruzsinszky]
MN12-L – 58-parameter meta-nonseparable gradient approximation functional by Peverati and Truhlar[Peverati and Truhlar(2012c)]
MN15-L – 58-parameter meta-nonseparable gradient approximation functional by Yu, He, and Truhlar[Yu et al.(2016b)Yu, He, and Truhlar]
oTPSS* – oTPSS meta-GGA exchange + oTPSS meta-GGA correlation
PKZB* – PKZB meta-GGA exchange + PKZB meta-GGA correlation
SCAN* – SCAN meta-GGA exchange + SCAN meta-GGA correlation
t-HCTH (
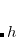 -HCTH) – 16-parameter functional by Boese and Handy[Boese and Handy(2002)]
-HCTH) – 16-parameter functional by Boese and Handy[Boese and Handy(2002)] TM* – TM meta-GGA exchange + TM meta-GGA correlation[Tao and Mo(2016)]
VSXC – 21-parameter functional by Voorhis and Scuseria[Van Voorhis and Scuseria(1998)]
Global Hybrid Generalized Gradient Approximation (GH GGA)
B3LYP – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange + 19% VWN1RPA LSDA correlation + 81% LYP GGA correlation[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch]
PBE0 – 25% HF exchange + 75% PBE GGA exchange + PBE GGA correlation[Adamo and Barone(1999)]
revPBE0 – 25% HF exchange + 75% revPBE GGA exchange + PBE GGA correlation
B97 – Becke’s original 10-parameter density functional with 19.43% HF exchange[Becke(1997)]
B1LYP – 25% HF exchange + 75% B88 GGA exchange + LYP GGA correlation[Adamo and Barone(1997)]
B1PW91 – 25% HF exchange + 75% B88 GGA exchange + PW91 GGA correlation[Adamo and Barone(1997)]
B3LYP5 – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange + 19% VWN5 LSDA correlation + 81% LYP GGA correlation[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch]
B3P86 – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange+ 19% VWN1RPA LSDA correlation + 81% P86 GGA correlation
B1LYP – 25% HF exchange + 75% B88 GGA exchange + LYP GGA correlation[Adamo and Barone(1997)]
B1PW91 – 25% HF exchange + 75% B88 GGA exchange + PW91 GGA correlation[Adamo and Barone(1997)]
B3LYP5 – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange + 19% VWN5 LSDA correlation + 81% LYP GGA correlation[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch]
B3P86 – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange+ 19% VWN1RPA LSDA correlation + 81% P86 GGA correlation
B3PW91 – 20% HF exchange + 8% Slater LSDA exchange + 72% B88 GGA exchange+ 19% PW92 LSDA correlation + 81% PW91 GGA correlation[Becke(1993)]
B5050LYP – 50% HF exchange + 8% Slater LSDA exchange + 42% B88 GGA exchange + 19% VWN5 LSDA correlation + 81% LYP GGA correlation[Shao et al.(2003)Shao, Head-Gordon, and Krylov]
B97-1 – Self-consistent parameterization of Becke’s B97 density functional with 21% HF exchange[Hamprecht et al.(1998)Hamprecht, Cohen, Tozer, and Handy]
B97-2 – Re-parameterization of B97 by Tozer and coworkers with 21% HF exchange[Wilson et al.(2001)Wilson, Bradley, and Tozer]
B97-3 – 16-parameter version of B97 by Keal and Tozer with
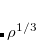 26.93% HF exchange[Keal and Tozer(2005)]
26.93% HF exchange[Keal and Tozer(2005)] B97-K – Re-parameterization of B97 for kinetics by Boese and Martin with 42% HF exchange[Boese and Martin(2004)]
BHHLYP – 50% HF exchange + 50% B88 GGA exchange + LYP GGA correlation
HFLYP* – 100% HF exchange + LYP GGA correlation
MPW1K – 42.8% HF exchange + 57.2% mPW91 GGA exchange + PW91 GGA correlation[Lynch et al.(2000)Lynch, Fast, Harris, and Truhlar]
MPW1LYP – 25% HF exchange + 75% mPW91 GGA exchange + LYP GGA correlation[Adamo and Barone(1998)]
MPW1PBE – 25% HF exchange + 75% mPW91 GGA exchange + PBE GGA correlation[Adamo and Barone(1998)]
MPW1PW91 – 25% HF exchange + 75% mPW91 GGA exchange + PW91 GGA correlation[Adamo and Barone(1998)]
O3LYP – 11.61% HF exchange +
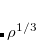 7.1% Slater LSDA exchange + 81.33% OPTX GGA exchange + 19% VWN5 LSDA correlation + 81% LYP GGA correlation[Hoe et al.(2001)Hoe, Cohen, and Handy]
7.1% Slater LSDA exchange + 81.33% OPTX GGA exchange + 19% VWN5 LSDA correlation + 81% LYP GGA correlation[Hoe et al.(2001)Hoe, Cohen, and Handy] PBEh-3c – Low-cost composite scheme of Grimme and coworkers for use with the def2-mSVP basis set only[Grimme et al.(2015)Grimme, Brandenburg, Bannwarth, and Hansen]
PBE50 – 50% HF exchange + 50% PBE GGA exchange + PBE GGA correlation[Bernard et al.(2012b)Bernard, Shao, and Krylov]
SOGGA11-X – 21-parameter functional with 40.15% HF exchange by Peverati and Truhlar[Peverati and Truhlar(2011a)]
WC04 – Hybrid density functional optimized for the computation of
 C chemical shifts[Wiitala et al.(2006)Wiitala, Hoye, and Cramer]
C chemical shifts[Wiitala et al.(2006)Wiitala, Hoye, and Cramer] WP04 – Hybrid density functional optimized for the computation of
 H chemical shifts[Wiitala et al.(2006)Wiitala, Hoye, and Cramer]
H chemical shifts[Wiitala et al.(2006)Wiitala, Hoye, and Cramer] X3LYP – 21.8% HF exchange + 7.3% Slater LSDA exchange +
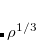 54.24% B88 GGA exchange +
54.24% B88 GGA exchange + 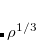 16.66% PW91 GGA exchange + 12.9% VWN1RPA LSDA correlation + 87.1% LYP GGA correlation[Xu and Goddard III(2004)]
16.66% PW91 GGA exchange + 12.9% VWN1RPA LSDA correlation + 87.1% LYP GGA correlation[Xu and Goddard III(2004)]
Global Hybrid Meta-Generalized Gradient Approximation (GH meta-GGA)
M06-2X – 29-parameter functional with 54% HF exchange by Zhao and Truhlar[Zhao and Truhlar(2008)]
M08-HX – 47-parameter functional with 52.23% HF exchange by Zhao and Truhlar[Zhao and Truhlar(2007)]
TPSSh – 10% HF exchange + 90% TPSS meta-GGA exchange + TPSS meta-GGA correlation[Staroverov et al.(2003)Staroverov, Scuseria, Tao, and Perdew]
revTPSSh – 10% HF exchange + 90% revTPSS meta-GGA exchange + revTPSS meta-GGA correlation[Csonka et al.(2010)Csonka, Perdew, and Ruzsinszky]
B1B95 – 28% HF exchange + 72% B88 GGA exchange + B95 meta-GGA correlation[Becke(1996)]
B3TLAP – 17.13% HF exchange + 9.66% Slater LSDA exchange + 72.6% B88 GGA exchange + PK06 meta-GGA correlation[Proynov and Kong(2007), Proynov and Kong(2008)]
BB1K – 42% HF exchange + 58% B88 GGA exchange + B95 meta-GGA correlation[Zhao et al.(2004)Zhao, Lynch, and Truhlar]
BMK – Boese-Martin functional for kinetics with 42% HF exchange[Boese and Martin(2004)]
dlDF – Dispersion-less density functional (based on the M05-2X functional form) by Szalewicz and coworkers[Pernal et al.(2009)Pernal, Podeszwa, Patkowski, and Szalewicz]
M05 – 22-parameter functional with 28% HF exchange by Zhao, Schultz, and Truhlar[Zhao et al.(2005)Zhao, Schultz, and Truhlar]
M05-2X – 19-parameter functional with 56% HF exchange by Zhao, Schultz, and Truhlar[Zhao et al.(2006)Zhao, Schultz, and Truhlar]
M06 – 33-parameter functional with 27% HF exchange by Zhao and Truhlar[Zhao and Truhlar(2008)]
M06-HF – 32-parameter functional with 100% HF exchange by Zhao and Truhlar[Zhao and Truhlar(2006b)]
M08-SO – 44-parameter functional with 56.79% HF exchange by Zhao and Truhlar[Zhao and Truhlar(2007)]
MGGA_MS2h – 9% HF exchange + 91 % MGGA_MS2 meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2013)Sun, Haunschild, Xiao, Bulik, Scuseria, and Perdew]
MGGA_MVSh – 25% HF exchange + 75 % MGGA_MVS meta-GGA exchange + regTPSS GGA correlation[Sun et al.(2015a)Sun, Perdew, and Ruzsinszky]
MN15 – 59-parameter functional with 44% HF exchange by Truhlar and coworkers[Yu et al.(2016a)Yu, He, Li, and Truhlar]
MPW1B95 – 31% HF exchange + 69% mPW91 GGA exchange + B95 meta-GGA correlation[Zhao and Truhlar(2004)]
MPWB1K – 44% HF exchange + 56% mPW91 GGA exchange + B95 meta-GGA correlation[Zhao and Truhlar(2004)]
PW6B95 – 6-parameter combination of 28 % HF exchange, 72 % optimized PW91 GGA exchange, and re-optimized B95 meta-GGA correlation by Zhao and Truhlar[Zhao and Truhlar(2005)]
PWB6K – 6-parameter combination of 46 % HF exchange, 54 % optimized PW91 GGA exchange, and re-optimized B95 meta-GGA correlation by Zhao and Truhlar[Zhao and Truhlar(2005)]
SCAN0 – 25% HF exchange + 75% SCAN meta-GGA exchange + SCAN meta-GGA correlation[Hui and Chai(2016)]
t-HCTHh (
 -HCTHh) – 17-parameter functional with 15% HF exchange by Boese and Handy[Boese and Handy(2002)]
-HCTHh) – 17-parameter functional with 15% HF exchange by Boese and Handy[Boese and Handy(2002)] TPSS0 – 25% HF exchange + 75% TPSS meta-GGA exchange + TPSS meta-GGA correlation[Grimme(2005)]
Range-Separated Hybrid Generalized Gradient Approximation (RSH GGA)
wB97X-V (
 B97X-V) – 10-parameter combinatorially-optimized, dispersion-corrected (VV10) functional with 16.7% SR HF exchange, 100% LR HF exchange, and
B97X-V) – 10-parameter combinatorially-optimized, dispersion-corrected (VV10) functional with 16.7% SR HF exchange, 100% LR HF exchange, and 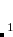 [Mardirossian and Head-Gordon(2014)]
[Mardirossian and Head-Gordon(2014)] wB97X-D3 (
 B97X-D3) – 16-parameter dispersion-corrected (DFT-D3(0)) functional with
B97X-D3) – 16-parameter dispersion-corrected (DFT-D3(0)) functional with 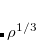 19.57% SR HF exchange, 100% LR HF exchange, and
19.57% SR HF exchange, 100% LR HF exchange, and 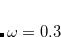 [Lin et al.(2013)Lin, Li, Mao, and Chai]
[Lin et al.(2013)Lin, Li, Mao, and Chai] wB97X-D (
 B97X-D) – 15-parameter dispersion-corrected (DFT-CHG) functional with
B97X-D) – 15-parameter dispersion-corrected (DFT-CHG) functional with 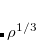 22.2% SR HF exchange, 100% LR HF exchange, and
22.2% SR HF exchange, 100% LR HF exchange, and 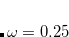 [Chai and Head-Gordon(2008b)]
[Chai and Head-Gordon(2008b)] CAM-B3LYP – Coulomb-attenuating method functional by Handy and coworkers[Yanai et al.(2004)Yanai, Tew, and Handy]
CAM-QTP00 – Re-parameterized CAM-B3LYP designed to satisfy the IP-theorem for all occupied orbitals of the water molecule[Verma and Bartlett(2014)]
CAM-QTP01 – Re-parameterized CAM-B3LYP optimized to satisfy the valence IPs of the water molecule, 34 excitation states, and G2-1 atomization energies[Jin and Bartlett(2016)]
HSE-HJS – Screened-exchange “HSE06” functional with 25% SR HF exchange, 0% LR HF exchange, and
 =0.11, using the updated HJS PBE exchange hole model[Krukau et al.(2006)Krukau, Vydrov, Izmaylov, and Scuseria, Henderson et al.(2008)Henderson, Janesko, and Scuseria]
=0.11, using the updated HJS PBE exchange hole model[Krukau et al.(2006)Krukau, Vydrov, Izmaylov, and Scuseria, Henderson et al.(2008)Henderson, Janesko, and Scuseria] LC-rVV10* – LC-VV10 density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon]
LC-VV10 – 0% SR HF exchange + 100% LR HF exchange +
 PBE GGA exchange + PBE GGA correlation + VV10 non-local correlation (
PBE GGA exchange + PBE GGA correlation + VV10 non-local correlation ( =0.45)[Vydrov and Van Voorhis(2010b)]
=0.45)[Vydrov and Van Voorhis(2010b)] LC-wPBE08 (LC-
 PBE08) – 0% SR HF exchange + 100% LR HF exchange +
PBE08) – 0% SR HF exchange + 100% LR HF exchange +  PBE GGA exchange + PBE GGA correlation (
PBE GGA exchange + PBE GGA correlation ( =0.45)[Weintraub et al.(2009)Weintraub, Henderson, and Scuseria]
=0.45)[Weintraub et al.(2009)Weintraub, Henderson, and Scuseria] LRC-BOP (LRC-
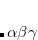 BOP)– 0% SR HF exchange + 100% LR HF exchange + muB88 GGA exchange + BOP GGA correlation (
BOP)– 0% SR HF exchange + 100% LR HF exchange + muB88 GGA exchange + BOP GGA correlation ( =0.47)[Song et al.(2007)Song, Hirosawa, Tsuneda, and Hirao]
=0.47)[Song et al.(2007)Song, Hirosawa, Tsuneda, and Hirao] LRC-wPBE (LRC-
 PBE) – 0% SR HF exchange + 100% LR HF exchange +
PBE) – 0% SR HF exchange + 100% LR HF exchange +  PBE GGA exchange + PBE GGA correlation (
PBE GGA exchange + PBE GGA correlation ( =0.3)[Rohrdanz and Herbert(2008)]
=0.3)[Rohrdanz and Herbert(2008)] LRC-wPBEh (LRC-
 PBEh) – 20% SR HF exchange + 100% LR HF exchange + 80%
PBEh) – 20% SR HF exchange + 100% LR HF exchange + 80%  PBE GGA exchange + PBE GGA correlation (
PBE GGA exchange + PBE GGA correlation ( =0.2)[Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert]
=0.2)[Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] N12-SX – 26-parameter non-separable GGA with 25% SR HF exchange, 0% LR HF exchange, and
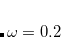 [Peverati and Truhlar(2012d)]
[Peverati and Truhlar(2012d)] rCAM-B3LYP – Re-fit CAM-B3LYP with the goal of minimizing many-electron self-interaction error[Cohen et al.(2007b)Cohen, Mori-Sánchez, and Yang]
wB97 (
 B97) – 13-parameter functional with 0% SR HF exchange, 100% LR HF exchange, and
B97) – 13-parameter functional with 0% SR HF exchange, 100% LR HF exchange, and 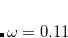 [Chai and Head-Gordon(2008a)]
[Chai and Head-Gordon(2008a)] wB97X (
 B97X) – 14-parameter functional with
B97X) – 14-parameter functional with 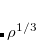 15.77% SR HF exchange, 100% LR HF exchange, and
15.77% SR HF exchange, 100% LR HF exchange, and 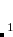 [Chai and Head-Gordon(2008a)]
[Chai and Head-Gordon(2008a)] wB97X-rV* (
 B97X-rV) –
B97X-rV) –  B97X-V density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon]
B97X-V density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon]
Range-Separated Hybrid Meta-Generalized Gradient Approximation (RSH meta-GGA)
wB97M-V (
 B97M-V) – 12-parameter combinatorially-optimized, dispersion-corrected (VV10) functional with 15% SR HF exchange, 100% LR HF exchange, and
B97M-V) – 12-parameter combinatorially-optimized, dispersion-corrected (VV10) functional with 15% SR HF exchange, 100% LR HF exchange, and 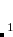 [Mardirossian and Head-Gordon(2016)]
[Mardirossian and Head-Gordon(2016)] M11 – 40-parameter functional with 42.8% SR HF exchange, 100% LR HF exchange, and
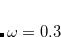 [Peverati and Truhlar(2011b)]
[Peverati and Truhlar(2011b)] MN12-SX – 58-parameter non-separable meta-GGA with 25% SR HF exchange, 0% LR HF exchange, and
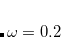 [Peverati and Truhlar(2012d)]
[Peverati and Truhlar(2012d)] wB97M-rV* (
 B97X-rV) –
B97X-rV) –  B97M-V density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon]
B97M-V density functional with the VV10 NLC functional replaced by the rVV10 NLC functional[Mardirossian et al.(2017)Mardirossian, Pestana, Womack, Skylaris, Head-Gordon, and Head-Gordon] wM05-D (
 M05-D) – 21-parameter dispersion-corrected (DFT-CHG) functional with
M05-D) – 21-parameter dispersion-corrected (DFT-CHG) functional with 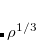 36.96% SR HF exchange, 100% LR HF exchange, and
36.96% SR HF exchange, 100% LR HF exchange, and 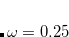 [Lin et al.(2012)Lin, Tsai, Li, and Chai]
[Lin et al.(2012)Lin, Tsai, Li, and Chai] wM06-D3 (
 M06-D3) – 25-parameter dispersion-corrected [DFT-D3(0)] functional with
M06-D3) – 25-parameter dispersion-corrected [DFT-D3(0)] functional with 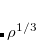 27.15% SR HF exchange, 100% LR HF exchange, and
27.15% SR HF exchange, 100% LR HF exchange, and  [Lin et al.(2013)Lin, Li, Mao, and Chai]
[Lin et al.(2013)Lin, Li, Mao, and Chai]
Double Hybrid Generalized Gradient Approximation (DH GGA)
Note: In order to use the resolution-of-the-identity approximation for the MP2 component, specify an auxiliary basis set with the $rem variable AUX_BASIS
DSD-PBEPBE-D3 – 68% HF exchange + 32% PBE GGA exchange + 49% PBE GGA correlation + 13% SS MP2 correlation + 55% OS MP2 correlation with DFT-D3(BJ) tail[Kozuch and Martin(2013)]
wB97X-2(LP) (
 B97X-2(LP)) – 13-parameter functional with
B97X-2(LP)) – 13-parameter functional with 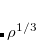 67.88% SR HF exchange, 100% LR HF exchange,
67.88% SR HF exchange, 100% LR HF exchange, 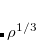 58.16% SS MP2 correlation,
58.16% SS MP2 correlation, 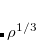 47.80% OS MP2 correlation, and
47.80% OS MP2 correlation, and  [Chai and Head-Gordon(2009)]
[Chai and Head-Gordon(2009)] wB97X-2(TQZ) (
 B97X-2(TQZ)) – 13-parameter functional with
B97X-2(TQZ)) – 13-parameter functional with 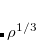 63.62% SR HF exchange, 100% LR HF exchange,
63.62% SR HF exchange, 100% LR HF exchange, 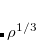 52.93% SS MP2 correlation,
52.93% SS MP2 correlation, 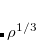 44.71% OS MP2 correlation, and
44.71% OS MP2 correlation, and  [Chai and Head-Gordon(2009)]
[Chai and Head-Gordon(2009)] XYG3 – 80.33% HF exchange - 1.4% Slater LSDA exchange + 21.07% B88 GGA exchange + 67.89% LYP GGA correlation + 32.11% MP2 correlation (evaluated with B3LYP orbitals)[Zhang et al.(2009)Zhang, Xu, and Goddard III]
XYGJ-OS – 77.31% HF exchange + 22.69% Slater LSDA exchange + 23.09% VWN1RPA LSDA correlation + 27.54% LYP GGA correlation + 43.64% OS MP2 correlation (evaluated with B3LYP orbitals)[Zhang et al.(2011)Zhang, Xin, Jung, and Goddard III]
B2PLYP – 53% HF exchange + 47% B88 GGA exchange + 73% LYP GGA correlation + 27% MP2 correlation[Grimme(2006a)]
B2GPPLYP – 65% HF exchange + 35% B88 GGA exchange + 64% LYP GGA correlation + 36% MP2 correlation[Karton et al.(2008)Karton, Tarnopolsky, Lamère, Schatz, and Martin]
DSD-PBEP86-D3 – 69% HF exchange + 31% PBE GGA exchange + 44% P86 GGA correlation + 22% SS MP2 correlation + 52% OS MP2 correlation with DFT-D3(BJ) tail[Kozuch and Martin(2013)]
LS1DH-PBE – 75% HF exchange + 25% PBE GGA exchange + 57.8125% PBE GGA correlation + 42.1875% MP2 correlation[Toulouse et al.(2011)Toulouse, Sharkas., Brémond, and Adamo]
PBE-QIDH – 69.3361% HF exchange + 30.6639% PBE GGA exchange + 66.6667% PBE GGA correlation + 33.3333% MP2 correlation[Brémond et al.(2014)Brémond, Sancho-Garc
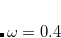 a, Pérez-Jiménez, and Adamo]
a, Pérez-Jiménez, and Adamo] PBE0-2 –
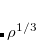 79.37% HF exchange +
79.37% HF exchange + 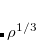 20.63% PBE GGA exchange + 50% PBE GGA correlation + 50% MP2 correlation[Chai and Mao(2012)]
20.63% PBE GGA exchange + 50% PBE GGA correlation + 50% MP2 correlation[Chai and Mao(2012)] PBE0-DH – 50% HF exchange + 50% PBE GGA exchange + 87.5% PBE GGA correlation + 12.5% MP2 correlation[Brémond and Adamo(2011)]
Double Hybrid Meta-Generalized Gradient Approximation (DH MGGA)
PTPSS-D3 – 50% HF exchange + 50% Re-Fit TPSS meta-GGA exchange + 62.5% Re-Fit TPSS meta-GGA correlation + 37.5% OS MP2 correlation with DFT-D3(0) tail[Goerigk and Grimme(2011)]
DSD-PBEB95-D3 – 66% HF exchange + 34% PBE GGA exchange + 55% B95 GGA correlation + 9% SS MP2 correlation + 46% OS MP2 correlation with DFT-D3(BJ) tail[Kozuch and Martin(2013)]
PWPB95-D3 – 50% HF exchange + 50% Re-Fit PW91 GGA exchange + 73.1% Re-Fit B95 meta-GGA correlation + 26.9% OS MP2 correlation with DFT-D3(0) tail[Goerigk and Grimme(2011)]
5.3.5 Specialized Functionals
SRC1-R1 – TDDFT short-range corrected functional (Equation 1 in Ref. Besley:2009a, 1st row atoms)
SRC1-R2 – TDDFT short-range corrected functional (Equation 1 in Ref. Besley:2009a, 2nd row atoms)
SRC2-R1 – TDDFT short-range corrected functional (Equation 2 in Ref. Besley:2009a, 1st row atoms)
SRC2-R2 – TDDFT short-range corrected functional (Equation 2 in Ref. Besley:2009a, 2nd row atoms)
BR89 – Becke-Roussel meta-GGA exchange functional modeled after the hydrogen atom[Becke and Roussel(1989)]
B94 – meta-GGA correlation functional by Becke that uses the BR89 exchange functional to compute the Coulomb potential[Becke(1994)]
B94hyb – modified version of the B94 correlation functional for use with the BR89B94hyb exchange-correlation functional[Becke(1994)]
BR89B94h – 15.4% HF exchange + 84.6% BR89 meta-GGA exchange + BR89hyb meta-GGA correlation[Becke(1994)]
BRSC – Exchange component of the original B05 exchange-correlation functional[Becke and Johnson(2005)]
MB05 – Exchange component of the modified B05 (BM05) exchange-correlation functional[Proynov et al.(2012a)Proynov, Liu, and Kong]
B05 – A full exact-exchange Kohn-Sham scheme of Becke that uses the exact-exchange energy density (RI) and accounts for static correlation[Becke and Johnson(2005), Proynov et al.(2010)Proynov, Shao, and Kong, Proynov et al.(2012b)Proynov, Liu, Shao, and Kong]
BM05 (XC) – Modified B05 hyper-GGA scheme that uses MB05 instead of BRSC as the exchange functional[Proynov et al.(2012a)Proynov, Liu, and Kong]
PSTS – Hyper-GGA (100% HF exchange) exchange-correlation functional of Perdew, Staroverov, Tao, and Scuseria[Perdew et al.(2008b)Perdew, Staroverov, Tao, and Scuseria]
MCY2 – Mori-Sánchez-Cohen-Yang adiabatic connection-based hyper-GGA exchange-correlation functional[Mori-Sánchez et al.(2006)Mori-Sánchez, Cohen, and Yang, Cohen et al.(2007a)Cohen, Mori-Sánchez, and Yang, Liu et al.(2012)Liu, Proynov, Yu, Furlani, and Kong]
5.3.6 User-Defined Density Functionals
Users can also request a customized density functional consisting of any linear combination of exchange and/or correlation functionals available in Q-Chem. A “general” density functional of this sort is requested by setting EXCHANGE = GEN and then specifying the functional by means of an $xc_functional input section consisting of one line for each desired exchange (X) or correlation (C) component of the functional, and having the format shown below.
$xc_functional
X exchange_symbol coefficient
X exchange_symbol coefficient
...
C correlation_symbol coefficient
C correlation_symbol coefficient
...
K coefficient
$end
Each line requires three variables: X or C to designate whether this is an exchange or correlation component; the symbolic representation of the functional, as would be used for the EXCHANGE or CORRELATION keywords variables as described above; and a real number coefficient for each component. Note that Hartree-Fock exchange can be designated either as “X" or as “K". Examples are shown below.
Example 5.44 Q-Chem input for H O with the B3tLap functional.
O with the B3tLap functional.
$molecule
0 1
O
H1 O oh
H2 O oh H1 hoh
oh = 0.97
hoh = 120.0
$end
$rem
EXCHANGE gen
CORRELATION none
BASIS g3large ! recommended for high accuracy
THRESH 14 ! and better convergence
$end
$xc_functional
X Becke 0.726
X S 0.0966
C PK06 1.0
K 0.1713
$end
Example 5.45 Q-Chem input for H O with the BR89B94hyb functional.
O with the BR89B94hyb functional.
$molecule
0 1
O
H1 O oh
H2 O oh H1 hoh
oh = 0.97
hoh = 120.0
$end
$rem
EXCHANGE gen
CORRELATION none
BASIS g3large ! recommended for high accuracy
THRESH 14 ! and better convergence
$end
$xc_functional
X BR89 0.846
C B94hyb 1.0
K 0.154
$end
The next two examples illustrate the use of the RI-B05 and RI-PSTS functionals. These are presently available only for single-point calculations, and convergence is greatly facilitated by obtaining converged SCF orbitals from, e.g., an LDA or HF calculation first. (LDA is used in the example below but HF can be substituted.) Use of the RI approximation (Section 6.6) requires specification of an auxiliary basis set.
Example 5.46 Q-Chem input of H using RI-B05.
using RI-B05.
$comment
H2, example of SP RI-B05. First do a well-converged LSD, G3LARGE is the
basis of choice for good accuracy. The input lines
PURECART 2222
SCF_GUESS CORE
are obligatory for the time being here.
$end
$molecule
0 1
H 0. 0. 0.0
H 0. 0. 0.7414
$end
$rem
SCF_GUESS core
METHOD lda
BASIS g3large
PURECART 2222
THRESH 14
INCDFT false
SYM_IGNORE true
SYMMETRY false
SCF_CONVERGENCE 9
$end
@@@
$comment
For the time being the following input lines are obligatory:
PURECART 2222
AUX_BASIS riB05-cc-pvtz
DFT_CUTOFFS 0
MAX_SCF_CYCLES 0
$end
$molecule
read
$end
$rem
SCF_GUESS read
EXCHANGE b05 ! or set to psts for ri-psts
PURECART 2222
BASIS g3large
AUX_BASIS rib05-cc-pvtz ! the aux basis for both RI-B05 and RI-PSTS
THRESH 4
PRINT_INPUT true
INCDFT false
SYM_IGNORE true
SYMMETRY false
MAX_SCF_CYCLES 0
DFT_CUTOFFS 0
$end

 OpenMP parallelization available
OpenMP parallelization available MPI parallelization available
MPI parallelization available