Q-Chem 5.1 User’s Manual

13.12 The XPol+SAPT (XSAPT) Method

13.12.1 Theory

XPol+SAPT, or “XSAPT”, was introduced by Jacobson and Herbert[Jacobson and Herbert(2011), Herbert et al.(2012)Herbert, Jacobson, Lao, and Rohrdanz] (later significantly extended by Lao and Herbert[Lao and Herbert(2012b), Lao and Herbert(2013), Lao and Herbert(2015), Lao and Herbert()]) as a low-scaling, systematically-improvable method for intermolecular interactions that could be applicable to large systems. The original idea was to replace the need for empirical parameters in the XPol method with on-the-fly evaluation of exchange-repulsion and dispersion interactions via pairwise-additive SAPT. Stated differently, XSAPT uses XPol to evaluate many-body (non-pairwise-additive) polarization effects, but then assumes that dispersion and exchange-repulsion interactions are pairwise additive, and evaluates them via pairwise SAPT0 or SAPT(KS) calculations. An overview of XSAPT-based methods can be found in Ref. Lao:2015.

The zeroth-order Hamiltonian for XSAPT is taken by the sum of fragment Fock operators defined by the XPol procedure, and the perturbation is the usual SAPT intermolecular perturbation [Eq. eq:pairwise_perturbation] less the intermolecular interactions contained in the XPol fragment Fock operators. A standard SAPT0 correction is then computed for each pair of monomers, using Eq. eq:SAPT_interaction in conjunction with the modified perturbation, to obtain dimer interaction energy $E_\ensuremath{\mathrm{}}{int}^{AB}$. The total XSAPT energy is then

  \begin{equation} \label{eq:XSAPT_ total_ E} E^{}_{\rm XSAPT} = \sum _ A \left( \sum _ a \Bigl [ 2\, \epsilon _ a^ A - \mathbf{c}_ a^\dagger ( \mathbf{J}^ A - \tfrac {1}{2}\mathbf{K}^ A)\mathbf{c}_ a\Bigr ] + E_\ensuremath{\mathrm{}}{nuc}^ A + \sum _{B>A} E_\ensuremath{\mathrm{}}{int}^{AB} \right) \; . \end{equation}   (13.38)

In this expression, we have removed the over-counting of two-electron interactions present in Hartree-Fock theory, effectively taking the intrafragment perturbation to first order. The generalization to a Kohn-Sham description of the monomers is straightforward, and is available in Q-Chem.

The inclusion of many-body polarization within the zeroth-order Hamiltonian makes the subsequent SAPT corrections less meaningful in terms of energy decomposition analysis. For instance, the first-order electrostatic correction in XSAPT is not the total electrostatic energy, since the former corrects for errors in the approximate electrostatic treatment at zeroth order (i.e., the electrostatic embedding). The dispersion correction may be less contaminated, since all of the XSAPT modifications to the traditional SAPT perturbation are one-electron operators and therefore the pairwise dispersion correction differs from its traditional SAPT analogue only insofar as the MOs are perturbed by the electrostatic embedding. This should be kept in mind when interpreting the output of an XSAPT calculation, although Lao and Herbert[Lao and Herbert(2013), Lao and Herbert(2015)] later proposed a many-body energy decomposition scheme for XSAPT that extends traditional SAPT energy decomposition to systems containing more than two monomers. (The aforementioned contamination problems are avoid through pairwise $\delta _\ensuremath{\mathrm{}}{int}^{\rm HF}$ corrections, comparing XSAPT results to traditional SAPT based on gas-phase monomers.) An XSAPT calculation is requested by setting the $rem variables XPOL and SAPT equal to TRUE and also setting XPOL_MPOL_ORDER = CHARGES.

Researchers who use Q-Chem’s XPol+SAPT code are asked to cite Refs. Jacobson:2011 and Herbert:2012. The latter contains a thorough discussion of the theory; a briefer summary can be found in Ref. Jacobson:2013.

Example 13.332  Example showing an XPol+SAPT0 calculation using ChElPG charges and CPHF. 

$rem
   BASIS            CC-PVDZ
   METHOD           HF
   XPOL             TRUE
   XPOL_MPOL_ORDER  CHARGES
   XPOL_CHARGE_TYPE QCHELPG
   SAPT             TRUE
   SAPT_CPHF        TRUE
   SYM_IGNORE       TRUE
$end

$molecule
0 1
-- formic acid
   0 1
   C  -1.888896 -0.179692  0.000000
   O  -1.493280  1.073689  0.000000
   O  -1.170435 -1.166590  0.000000
   H  -2.979488 -0.258829  0.000000
   H  -0.498833  1.107195  0.000000
-- formic acid
   0  1
   C  1.888896  0.179692  0.000000
   O  1.493280 -1.073689  0.000000
   O  1.170435  1.166590  0.000000
   H  2.979488  0.258829  0.000000
   H  0.498833 -1.107195  0.000000
$end

13.12.2 AO-XSAPT(KS)+aiD

As mentioned above, the dispersion components of the SAPT(KS) or XSAPT(KS) interaction energy are not of benchmark quality, even when tuned LRC functionals are employed.[Lao and Herbert(2014)] It happens that the dispersion and exchange-dispersion terms are also the most expensive part of a SAPT0 or SAPT(KS) calculation, scaling as the fourth and fifth powers of monomer size, respectively, whereas other terms are cubic scaling at worst. Both the efficiency and the accuracy of XSAPT(KS) calculations is thus improved if second-order dispersion ($E_\ensuremath{\mathrm{}}{disp}^{(2)} + E_\ensuremath{\mathrm{}}{exch-disp}^{(2)}$) is replaced by an empirical atom–atom dispersion potential. Because the dispersion energy is well-defined (and separable) within the SAPT formalism, it can be replaced by atom–atom dispersion potentials (of the $-C_6/R^6 - C_8/R^8 -\cdots $ variety) without any double-counting problem (as there is in empirical dispersion corrections for DFT). Moreover, these dispersion potentials can be fit directly to ab initio dispersion energies from high-level SAPT calculations [SAPT(DFT) and SAPT2+(3)], such that the dispersion potential, while it is classical in its form and does contain fitting parameters, can reasonably said to be an ab initio dispersion potential. To distinguish this approach from DFT-D (Section 5.7.2), which is more empirical and does have a potential double-counting problem, we now refer to this ab initio dispersion correction as “+aiD”,[Lao and Herbert()] although it was called simply “+D” in earlier work.[Lao and Herbert(2012b), Lao and Herbert(2013), Lao and Herbert(2015)] The composite method is called XSAPT(KS)+aiD; see Ref. Lao:2013 for an overview. A more efficient, atomic orbital (AO) implementation was reported quite recently,[Lao and Herbert()] extending the method to supramolecular complexes containing large monomers.

An XSAPT(KS)+aiD calculation is requested by setting SAPT_AO and SAPT_DISP_CORR equal to TRUE. There are three versions of the ab initio the dispersion potential: “first generation" (+aiD1),[Lao and Herbert(2012b)] second-generation (+aiD2),[Lao and Herbert(2013)] and third-generation (+aiD3) version.[Lao and Herbert(2015)] The user can select amongst these using the SAPT_DISP_VERSION $rem variable. Although all three versions exhibit similar performance for total interaction energies,[Lao and Herbert(2015)] only the +aiD2 and +aiD3 potentials were fit directly to ab initio dispersion data (rather than being fit to reproduce interaction energies themselves), and they do a much better job of reproducing individual energy components, as compared to +aiD1.[Lao and Herbert(2013), Lao and Herbert(2015)] The latter succeeds by error cancellation amongst the energy components and is not recommended. The difference between +aiD2 and +aiD3 is a larger training set for the latter, which was designed to afford better coverage of 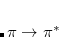$\pi $-stacked systems. The +aiD3 correction is the recommended one.

As with XPol, the XSAPT and XSAPT(KS)+aiD methods do not function with a solvation model or with external changes. Only single-point energies are available, and frozen orbitals orbitals are not allowed. Both restricted and unrestricted versions are available. Researchers who use XSAPT(KS)+aiD are asked to cite Ref. Lao:2012b for +aiD1, Ref. Lao:2013 for +aiD2, or Ref. Lao:2015 for +aiD3. The AO implementation of XSAPT is described in Ref. Lao:2018.

SAPT_AO

Request an atomic-orbital version of SAPT.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

TRUE

Use the AO version of SAPT.

FALSE

Use the MO version of SAPT.


RECOMMENDATION:

Use the AO version, which exhibits ${O}(N^3)$ scaling without significant memory bottlenecks.


SAPT_DISP_CORR

Request an empirical dispersion potential instead of calculating $E_{\text {disp}}^{(2)}$ and $E_{\text {exch-disp}}^{(2)}$ directly.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

TRUE

Use a dispersion force field.

FALSE

Calculate $E_{\text {disp}}^{(2)}$ and $E_{\text {exch-disp}}^{(2)}$.


RECOMMENDATION:

Dispersion potentials combined with AO-SAPT reduces the scaling from ${O}(N^5)$ to ${O}(N^3)$ with respect to monomer size, and second-order dispersion is not very accurate anyway.


SAPT_DISP_VERSION

Controls which dispersion potential is used for SAPT.


TYPE:

INTEGER


DEFAULT:

3


OPTIONS:

1

Use the “first generation” (+aiD1) dispersion potential.[Lao and Herbert(2012b)]

2

Use the “second generation” (+aiD2) dispersion potential.[Lao and Herbert(2013)]

3

Use the “third generation” (+aiD3) dispersion potentials.[Lao and Herbert(2015)]


RECOMMENDATION:

Use +aiD3. The second- and third-generation versions were parameterized using ab initio dispersion data and afford accurate energy components, in addition to accurate total interaction energies. The third-generation version was parameterized using an expanded data set designed to reduce some large errors observed for $\pi $-stacked complexes using +aiD2.


Example 13.333  AO-XSAPT(KS)+D3 calculation of water-water interaction. 

$rem
   SYM_IGNORE         true
   EXCHANGE           gen
   BASIS              aug-cc-pVTZ
   XPOL               true ! must be set to true for sapt jobs too
   XPOL_MPOL_ORDER    charges 
   XPOL_CHARGE_TYPE   qchelpg  
   XPOL_OMEGA         true
   XPOL_PRINT         3
   SAPT_PRINT         3
   SAPT               true
   SAPT_AO            true
   SAPT_ORDER         2          ! can be set to 1, ELST or RSPT
   SAPT_BASIS         projected ! monomer, dimer (if only 2 monomers), or projected
   SAPT_DISP_CORR     true
   SAPT_DISP_VERSION  3
   MEM_TOTAL          46000
   MEM_STATIC         4000
   AO2MO_DISK         35000
   THRESH             12
   SCF_CONVERGENCE    7
   LRC_DFT            true
   CHELPG             true
   CHELPG_DX          5
   CHELPG_HEAD        30
   CHELPG_H           110
   CHELPG_HA          590
$end

$xc_functional
   x   wPBE   1.0
   c   PBE   1.0
$end

$lrc_omega
   502
   502
$end

$molecule 
0 1
--
   0 1
   O  -1.551007  -0.114520   0.000000
   H  -1.934259   0.762503   0.000000
   H  -0.599677   0.040712   0.000000
--
   0 1
   O   1.350625   0.111469   0.000000
   H   1.680398  -0.373741  -0.758561
   H   1.680398  -0.373741   0.758561
$end