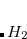13.11 Symmetry-Adapted Perturbation Theory (SAPT)
13.11.1 Theory
Symmetry-adapted perturbation theory (SAPT) is a theory of intermolecular interactions. When computing intermolecular interaction energies one typically computes the energy of two molecules infinitely separated and in contact, then computes the interaction energy by subtraction. SAPT, in contrast, is a perturbative expression for the interaction energy itself. The various terms in the perturbation series are physically meaningful, and this decomposition of the interaction energy can aid in the interpretation of the results. A brief overview of the theory is given below; for additional technical details, the reader is referred to Jeziorski et al..[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] Additional context can be found in a pair of more recent review articles.[Szalewicz(2012), Hohenstein and Sherrill(2012)]
In SAPT, the Hamiltonian for the  dimer is written as
dimer is written as
 |
(13.25) |
where  and
and  are Møller-Plesset fluctuation operators for fragments
are Møller-Plesset fluctuation operators for fragments  and
and 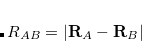 , whereas
, whereas  consists of the intermolecular Coulomb operators. This part of the perturbation is conveniently expressed as
consists of the intermolecular Coulomb operators. This part of the perturbation is conveniently expressed as
 |
(13.26) |
with
 |
(13.27) |
The quantity  is the nuclear interaction energy between the two fragments and
is the nuclear interaction energy between the two fragments and
 |
(13.28) |
describes the interaction of electron  with nucleus
with nucleus  .
.
Starting from a zeroth-order Hamiltonian  and zeroth-order wave functions that are direct products of monomer wave functions,
and zeroth-order wave functions that are direct products of monomer wave functions,  , the SAPT approach is based on a symmetrized Rayleigh-Schrödinger perturbation expansion[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] with respect to the perturbation parameters
, the SAPT approach is based on a symmetrized Rayleigh-Schrödinger perturbation expansion[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] with respect to the perturbation parameters 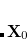 ,
,  , and
, and  in Eq. eq:H_SAPT. The resulting interaction energy can be expressed as[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
in Eq. eq:H_SAPT. The resulting interaction energy can be expressed as[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
 |
(13.29) |
Because it makes no sense to treat  and
and  at different orders of perturbation theory, there are only two indices in this expansion:
at different orders of perturbation theory, there are only two indices in this expansion: 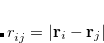 for the monomer fluctuations potentials and
for the monomer fluctuations potentials and  for the intermolecular perturbation. The terms
for the intermolecular perturbation. The terms  are known collectively as the polarization expansion, and these are precisely the same terms that would appear in ordinary Rayleigh-Schrödinger perturbation theory, which is valid when the monomers are well-separated. The polarization expansion contains electrostatic, induction and dispersion interactions, but in the symmetrized Rayleigh-Schrödinger expansion, each term
are known collectively as the polarization expansion, and these are precisely the same terms that would appear in ordinary Rayleigh-Schrödinger perturbation theory, which is valid when the monomers are well-separated. The polarization expansion contains electrostatic, induction and dispersion interactions, but in the symmetrized Rayleigh-Schrödinger expansion, each term  has a corresponding exchange term,
has a corresponding exchange term,  , that arises from an anti-symmetrizer
, that arises from an anti-symmetrizer  that is introduced in order to project away the Pauli-forbidden components of the interaction energy that would otherwise appear.[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
that is introduced in order to project away the Pauli-forbidden components of the interaction energy that would otherwise appear.[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
The version of SAPT that is implemented in Q-Chem assumes that  , an approach that is usually called SAPT0.[Hohenstein and Sherrill(2012)] Within the SAPT0 formalism, the interaction energy is formally expressed by the following symmetrized Rayleigh-Schrödinger expansion:[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
, an approach that is usually called SAPT0.[Hohenstein and Sherrill(2012)] Within the SAPT0 formalism, the interaction energy is formally expressed by the following symmetrized Rayleigh-Schrödinger expansion:[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
 |
(13.30) |
The anti-symmetrizer  in this expression can be written as
in this expression can be written as
 |
(13.31) |
where  and
and  are anti-symmetrizers for the two monomers and
are anti-symmetrizers for the two monomers and  is a sum of all one-electron exchange operators between the two monomers. The operator
is a sum of all one-electron exchange operators between the two monomers. The operator  in Eq. eq:AB_antisymmetrizer denotes all of the three-electron and higher-order exchanges. This operator is neglected in what is known as the “single-exchange” approximation,[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] which is expected to be quite accurate at typical van der Waals and larger intermolecular separations, but sometimes breaks down at smaller intermolecular separations.[Lao and Herbert(2012a)]
in Eq. eq:AB_antisymmetrizer denotes all of the three-electron and higher-order exchanges. This operator is neglected in what is known as the “single-exchange” approximation,[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] which is expected to be quite accurate at typical van der Waals and larger intermolecular separations, but sometimes breaks down at smaller intermolecular separations.[Lao and Herbert(2012a)]
Only terms up to  in Eq. eq:E(SRS)—that is, second order in the intermolecular interaction—have been implemented in Q-Chem. It is common to relabel these low-order terms in the following way [cf. Eq. eq:triple_pert]:
in Eq. eq:E(SRS)—that is, second order in the intermolecular interaction—have been implemented in Q-Chem. It is common to relabel these low-order terms in the following way [cf. Eq. eq:triple_pert]:
 |
(13.32) |
The electrostatic part of the first-order energy correction is denoted  and represents the Coulomb interaction between the two monomer electron densities.[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] The quantity
and represents the Coulomb interaction between the two monomer electron densities.[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] The quantity  is the corresponding first-order (i.e., Hartree-Fock) exchange correction. Explicit formulas for these corrections can be found in Ref. Jeziorski:1993. The second-order term from the polarization expansion, denoted
is the corresponding first-order (i.e., Hartree-Fock) exchange correction. Explicit formulas for these corrections can be found in Ref. Jeziorski:1993. The second-order term from the polarization expansion, denoted  in Eq. eq:SAPT_interaction, consists of a dispersion contribution (which arises for the first time at second order) as well as a second-order correction for induction. The latter can be written
in Eq. eq:SAPT_interaction, consists of a dispersion contribution (which arises for the first time at second order) as well as a second-order correction for induction. The latter can be written
 |
(13.33) |
where the notation  , for example, indicates that the frozen charge density of
, for example, indicates that the frozen charge density of 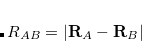 polarizes the density of
polarizes the density of  . In detail,
. In detail,
 |
(13.34) |
where
 |
(13.35) |
and  . The second term in Eq. eq:E(2)_ind, in which
. The second term in Eq. eq:E(2)_ind, in which  polarizes
polarizes 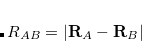 , is obtained by interchanging labels.[Jacobson and Herbert(2011)] The second-order dispersion correction has a form reminiscent of the MP2 correlation energy:
, is obtained by interchanging labels.[Jacobson and Herbert(2011)] The second-order dispersion correction has a form reminiscent of the MP2 correlation energy:
 |
(13.36) |
The induction and dispersion corrections both have accompanying exchange corrections (exchange-induction and exchange-dispersion).[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz]
The similarity between Eq. eq:E(2)_disp and the MP2 correlation energy means that SAPT jobs, like MP2 calculations, can be greatly accelerated using resolution-of-identity (RI) techniques, and an RI version of SAPT is available in Q-Chem. To use it, one must specify an auxiliary basis set. The same ones used for RI-MP2 work equally well for RI-SAPT, but one should always select the auxiliary basis set that is tailored for use with the primary basis of interest, as in the RI-MP2 examples in Section 6.6.1.
It is common to replace  and
and  in Eq. eq:SAPT_interaction with their “response” (
in Eq. eq:SAPT_interaction with their “response” ( ) analogues, which are the infinite-order correction for polarization arising from a frozen partner density.[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] Operationally, this substitution involves replacing the second-order induction amplitudes,
) analogues, which are the infinite-order correction for polarization arising from a frozen partner density.[Jeziorski et al.(1993)Jeziorski, Moszynski, Ratkiewicz, Rybak, Szalewicz, and Williams, Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz] Operationally, this substitution involves replacing the second-order induction amplitudes,  in Eq. eq:E(2)_ind_A<-B, with amplitudes obtained from solution of the coupled-perturbed Hartree-Fock equations.[Pople et al.(1979)Pople, Krishnan, Schlegel, and Binkley] (The perturbation is simply the electrostatic potential of the other monomer.) In addition, it is common to correct the SAPT0 binding energy for higher-order polarization effects by adding a correction term of the form[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz, Hohenstein and Sherrill(2012)]
in Eq. eq:E(2)_ind_A<-B, with amplitudes obtained from solution of the coupled-perturbed Hartree-Fock equations.[Pople et al.(1979)Pople, Krishnan, Schlegel, and Binkley] (The perturbation is simply the electrostatic potential of the other monomer.) In addition, it is common to correct the SAPT0 binding energy for higher-order polarization effects by adding a correction term of the form[Jeziorski et al.(1994)Jeziorski, Moszynski, and Szalewicz, Hohenstein and Sherrill(2012)]
 |
(13.37) |
to the interaction energy. Here,  is the counterpoise-corrected Hartree-Fock binding energy for
is the counterpoise-corrected Hartree-Fock binding energy for  . Both the response corrections and the
. Both the response corrections and the  correction are optionally available in Q-Chem’s implementation of SAPT.
correction are optionally available in Q-Chem’s implementation of SAPT.
It is tempting to replace Hartree-Fock MOs and eigenvalues in the SAPT0 formulas with their Kohn-Sham counterparts, as a low-cost means of introducing monomer electron correlation. The resulting procedure is known as SAPT(KS),[Williams and Chabalowski(2001)] and does offer an improvement on SAPT0 for some strongly hydrogen-bonded systems.[Herbert et al.(2012)Herbert, Jacobson, Lao, and Rohrdanz] Unfortunately, SAPT(KS) results are generally in poor agreement with benchmark dispersion energies,[Herbert et al.(2012)Herbert, Jacobson, Lao, and Rohrdanz] owing to incorrect asymptotic behavior of approximate exchange-correlation potentials.[Misquitta and Szalewicz(2002)] The dispersion energies can be greatly improved through the use of long-range corrected (LRC) functionals in which the range-separation parameter, 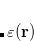 , is “tuned” so as to satisfy the condition
, is “tuned” so as to satisfy the condition  , where
, where  is the HOMO energy and “IP" represents the ionization potential.[Lao and Herbert(2014)] Monomer-specific values of
is the HOMO energy and “IP" represents the ionization potential.[Lao and Herbert(2014)] Monomer-specific values of 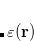 , tuned using the individual monomer IPs, substantially improve SAPT(KS) dispersion energies, though the results are still not of benchmark quality.[Lao and Herbert(2014)] Other components of the interaction energy, however, can be described quite accurately SAPT(KS) in conjunction with a tuned version of LRC-
, tuned using the individual monomer IPs, substantially improve SAPT(KS) dispersion energies, though the results are still not of benchmark quality.[Lao and Herbert(2014)] Other components of the interaction energy, however, can be described quite accurately SAPT(KS) in conjunction with a tuned version of LRC-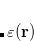 PBE.[Lao and Herbert(2014)] Use of monomer-specific
PBE.[Lao and Herbert(2014)] Use of monomer-specific 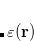 values is controlled by the variable XPOL_OMEGA in the $rem section, and individual values are entered via an $lrc_omega input section. The omega values of monomers at geometries optimized at RIMP2/aug-cc-pVDZ using LRC-
values is controlled by the variable XPOL_OMEGA in the $rem section, and individual values are entered via an $lrc_omega input section. The omega values of monomers at geometries optimized at RIMP2/aug-cc-pVDZ using LRC-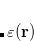 PBE functional based on
PBE functional based on  condition are listed in Table 13.1.
condition are listed in Table 13.1.
Monomer |
|
adenine |
0.271 |
2-aminopyridine |
0.293 |
benzene |
0.280 |
ethyne |
0.397 |
ethene |
0.359 |
methane |
0.454 |
formamide |
0.460 |
formic acid |
0.412 |
water |
0.502 |
HCN |
0.452 |
indole |
0.267 |
ammonia |
0.440 |
phenol |
0.292 |
pyrazine |
0.367 |
2-pyridoxine |
0.294 |
thymine |
0.284 |
uracil |
0.295 |
|
0.397 |
|
0.438 |
|
0.453 |
|
0.381 |
cyclopentane |
0.420 |
neopentane |
0.287 |
pentane |
0.365 |
peptide |
0.341 |
pyridine |
0.316 |
F |
0.480 |
Cl |
0.372 |
SO |
0.344 |
Li |
2.006 |
Na |
1.049 |
K |
0.755 |
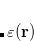 .
. Finally, some discussion of basis sets is warranted. Typically, SAPT calculations are performed in the so-called dimer-centered basis set (DCBS),[Williams et al.(1995)Williams, Mas, and Szalewicz] which means that the combined  basis set is used to calculate the zeroth-order wave functions for both
basis set is used to calculate the zeroth-order wave functions for both  and
and 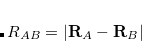 . This leads to the unusual situation that there are more MOs than basis functions: one set of occupied and virtual MOs for each monomer, both expanded in the same (dimer) AO basis. As an alternative to the DCBS, one might calculate
. This leads to the unusual situation that there are more MOs than basis functions: one set of occupied and virtual MOs for each monomer, both expanded in the same (dimer) AO basis. As an alternative to the DCBS, one might calculate  using only
using only  ’s basis functions (similarly for
’s basis functions (similarly for 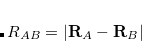 ), in which case the SAPT calculation is said to employ the monomer-centered basis set (MCBS).[Williams et al.(1995)Williams, Mas, and Szalewicz] However, MCBS results are generally of poorer quality. As an efficient alternative to the DCBS, Jacobson and Herbert[Jacobson and Herbert(2011)] introduced a projected (“proj”) or “pseudocanonicalized” basis set, borrowing an idea from dual-basis MP2 calculations.[Steele et al.(2006a)Steele, DiStasio, Jr., Shao, Kong, and Head-Gordon] In this approach, the SCF iterations are performed in the MCBS but then Fock matrices for fragments
), in which case the SAPT calculation is said to employ the monomer-centered basis set (MCBS).[Williams et al.(1995)Williams, Mas, and Szalewicz] However, MCBS results are generally of poorer quality. As an efficient alternative to the DCBS, Jacobson and Herbert[Jacobson and Herbert(2011)] introduced a projected (“proj”) or “pseudocanonicalized” basis set, borrowing an idea from dual-basis MP2 calculations.[Steele et al.(2006a)Steele, DiStasio, Jr., Shao, Kong, and Head-Gordon] In this approach, the SCF iterations are performed in the MCBS but then Fock matrices for fragments  and
and 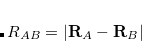 are constructed in the dimer (
are constructed in the dimer ( ) basis set and then pseudocanonicalized, meaning that the occupied-occupied and virtual-virtual blocks of these matrices are diagonalized. This procedure does not mix occupied and virtual orbitals, and thus leaves the fragment densities and zeroth-order fragment energies unchanged. However, it does provide a larger set of virtual orbitals that extend over the partner fragment. This larger virtual space is then used to evaluate the perturbative corrections. All three of these basis options (MCBS, DCBS, and projected basis) are available in Q-Chem.
) basis set and then pseudocanonicalized, meaning that the occupied-occupied and virtual-virtual blocks of these matrices are diagonalized. This procedure does not mix occupied and virtual orbitals, and thus leaves the fragment densities and zeroth-order fragment energies unchanged. However, it does provide a larger set of virtual orbitals that extend over the partner fragment. This larger virtual space is then used to evaluate the perturbative corrections. All three of these basis options (MCBS, DCBS, and projected basis) are available in Q-Chem.
13.11.2 Job Control for SAPT Calculations
Q-Chem’s implementation of SAPT0 was designed from the start as a correction for XPol calculations, a functionality that is described in Section 13.12. As such, a SAPT calculation is requested by setting both of the $rem variable SAPT and XPOL to TRUE. (Alternatively, one may set RISAPT=TRUE to use the RI version of SAPT.) If one wishes to perform a traditional SAPT calculation based on gas-phase SCF monomer wave functions rather than XPol monomer wave functions, then the $rem variable XPOL_MPOL_ORDER should be set to GAS.
SAPT energy components are printed separately at the end of a SAPT job. If EXCHANGE = HF, then the calculation corresponds to SAPT0, whereas a SAPT(KS) calculation is requested by specifying the desired density functional.
Note: (1) Meta-GGAs are not yet available for SAPT(KS) calculations when the projected (pseudocanonicalized) basis set is used. SAPT(KS) calculations can be performed with meta-GGAs using the monomer or dimer basis sets.
(2) Both closed- and open-shell (unrestricted) SAPT(KS) calculations are available.
(3) Frozen orbitals are not available for use with SAPT(KS).
Researchers who use Q-Chem’s SAPT code are asked to cite Refs. Jacobson:2011 and Herbert:2012.
SAPT
Requests a SAPT calculation.
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Run a SAPT calculation.
FALSE
Do not run SAPT.
RECOMMENDATION:
If SAPT is set to TRUE, one should also specify XPOL = TRUE and XPOL_MPOL_ORDER = GAS.
RISAPT
Requests an RI-SAPT calculation
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Compute four-index integrals using the RI approximation.
FALSE
Do not use RI.
RECOMMENDATION:
Set to TRUE if an appropriate auxiliary basis set is available, as RI-SAPT is much faster and affords negligible errors (as compared to ordinary SAPT) if the auxiliary basis set is matched to the primary basis set. (The former must be specified using AUX_BASIS.)
SAPT_ORDER
Selects the order in perturbation theory for a SAPT calculation.
TYPE:
STRING
DEFAULT:
SAPT2
OPTIONS:
SAPT1
First order SAPT.
SAPT2
Second order SAPT.
ELST
First-order Rayleigh-Schrödinger perturbation theory.
RSPT
Second-order Rayleigh-Schrödinger perturbation theory.
RECOMMENDATION:
SAPT2 is the most meaningful.
SAPT_EXCHANGE
Selects the type of first-order exchange that is used in a SAPT calculation.
TYPE:
STRING
DEFAULT:
S_SQUARED
OPTIONS:
S_SQUARED
Compute first order exchange in the single-exchange (“
") approximation.
S_INVERSE
Compute the exact first order exchange.
RECOMMENDATION:
The single-exchange approximation is expected to be adequate except possibly at very short intermolecular distances, and is somewhat faster to compute.
SAPT_BASIS
Controls the MO basis used for SAPT corrections.
TYPE:
STRING
DEFAULT:
MONOMER
OPTIONS:
MONOMER
Monomer-centered basis set (MCBS).
DIMER
Dimer-centered basis set (DCBS).
PROJECTED
Projected (pseudocanonicalized) basis set.
RECOMMENDATION:
The DCBS is more costly than the MCBS and can only be used with XPOL_MPOL_ORDER = GAS (i.e., it is not available for use with XPol). The PROJECTED choice is an efficient compromise that is available for use with XPol.
SAPT_CPHF
Requests that the second-order corrections
and
be replaced by their infinite-order “response” analogues,
and
.
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Evaluate the response corrections and use
and
FALSE
Omit these corrections and use
and
.
RECOMMENDATION:
Computing the response corrections requires solving CPHF equations for pair of monomers, which is somewhat expensive but may improve the accuracy when the monomers are polar.
SAPT_DSCF
Request the
correction
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Evaluate this correction.
FALSE
Omit this correction.
RECOMMENDATION:
Evaluating the
correction requires an SCF calculation on the entire (super)system. This corrections effectively yields a “Hartree-Fock plus dispersion” estimate of the interaction energy.
SAPT_PRINT
Controls level of printing in SAPT.
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:

Integer print level
RECOMMENDATION:
Larger values generate additional output.
Example 13.331 Example showing a SAPT0 calculation using the RI approximation in a DCBS.
$rem
BASIS AUG-CC-PVDZ
AUX_BASIS RIMP2-AUG-CC-PVDZ
METHOD HF
RISAPT TRUE
XPOL TRUE
XPOL_MPOL_ORDER GAS ! gas-phase monomer wave functions
SAPT_BASIS DIMER
SYM_IGNORE TRUE
$end
$molecule
0 1
-- formamide
0 1
C -2.018649 0.052883 0.000000
O -1.452200 1.143634 0.000000
N -1.407770 -1.142484 0.000000
H -1.964596 -1.977036 0.000000
H -0.387244 -1.207782 0.000000
H -3.117061 -0.013701 0.000000
-- formamide
0 1
C 2.018649 -0.052883 0.000000
O 1.452200 -1.143634 0.000000
N 1.407770 1.142484 0.000000
H 1.964596 1.977036 0.000000
H 0.387244 1.207782 0.000000
H 3.117061 0.013701 0.000000
$end
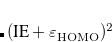 /
/