12.2 Chemical Solvent Models
Ab initio quantum chemistry makes possible the study of gas-phase molecular properties from first principles. In liquid solution, however, these properties may change significantly, especially in polar solvents. Although it is possible to model solvation effects by including explicit solvent molecules in the quantum-chemical calculation (e.g. a super-molecular cluster calculation, averaged over different configurations of the molecules in the first solvation shell), such calculations are very computationally demanding. Furthermore, cluster calculations typically do not afford accurate solvation energies, owing to the importance of long-range electrostatic interactions. Accurate prediction of solvation free energies is, however, crucial for modeling of chemical reactions and ligand/receptor interactions in solution.
Q-Chem contains several different implicit solvent models, which differ greatly in their level of sophistication. These are generally known as self-consistent reaction field (SCRF) models, because the continuum solvent establishes a “reaction field” (additional terms in the solute Hamiltonian) that depends upon the solute electron density, and must therefore be updated self-consistently during the iterative convergence of the wave function. The simplest and oldest of these models that is available in Q-Chem is the Kirkwood-Onsager model,[Kirkwood(1934), Onsager(1936), Kirkwood(1939)] in which the solute molecule is placed inside of a spherical cavity and its electrostatic potential is represented in terms of a single-center multipole expansion. More sophisticated models, which use a molecule-shaped cavity and the full molecular electrostatic potential, include the conductor-like screening model[Klamt and Schüürmann(1993)] (COSMO) and the closely related conductor-like PCM (C-PCM),[Truong and Stefanovich(1995), Barone and Cossi(1998), Cossi et al.(2003)Cossi, Rega, Scalmani, and Barone] along with the “surface and simulation of volume polarization for electrostatics” [SS(V)PE] model.[Chipman(2000)] The latter is also known as the “integral equation formalism” (IEF-PCM).[Cancès(1997), Cancès and Mennucci(2001)]
The C-PCM and IEF-PCM/SS(V)PE are examples of what are called “apparent surface charge” SCRF models, although the term polarizable continuum models (PCMs), as popularized by Tomasi and coworkers,[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] is now used almost universally to refer to this class of solvation models. Q-Chem employs a Switching/Gaussian or “SWIG” implementation of these PCMs.[Lange and Herbert(2010a), Lange and Herbert(2010b), Lange and Herbert(2011), Herbert and Lange(2016), Lange et al.()Lange, Herbert, Albrecht, and Herbert] This approach resolves a long-standing—though little-publicized—problem with standard PCMs, namely, that the boundary-element methods used to discretize the solute/continuum interface may lead to discontinuities in the potential energy surface for the solute molecule. These discontinuities inhibit convergence of geometry optimizations, introduce serious artifacts in vibrational frequency calculations, and make ab initio molecular dynamics calculations virtually impossible.[Lange and Herbert(2010a), Lange and Herbert(2010b)] In contrast, Q-Chem’s SWIG PCMs afford potential energy surfaces that are rigorously continuous and smooth. Unlike earlier attempts to obtain smooth PCMs, the SWIG approach largely preserves the properties of the underlying integral-equation solvent models, so that solvation energies and molecular surface areas are hardly affected by the smoothing procedure.
Other solvent models available in Q-Chem include the “Langevin dipoles” model;[Florián and Warshel(1997), Florián and Warshel(1999)] as well as versions 8 and 12 of the SM models, and the SMD model, developed at the University of Minnesota.[Marenich et al.(2007)Marenich, Olson, Kelly, Cramer, and Truhlar, Marenich et al.(2013)Marenich, Cramer, and Truhlar, Marenich et al.(2009)Marenich, Olson, Kelly, Cramer, and Truhlar] SM8 and SM12 are based upon the generalized Born method for electrostatics, augmented with atomic surface tensions intended to capture non-electrostatic effects (cavitation, dispersion, exchange repulsion, and changes in solvent structure). Empirical corrections of this sort are also available for the PCMs mentioned above, but within SM8 and SM12 these parameters have been optimized to reproduce experimental solvation energies. SMD (where the “D” is for “density") combines IEF-PCM with the non-electrostatic corrections, but because the electrostatics is based on the density rather than atomic point charges, it is supported for arbitrary basis sets whereas SM8 and SM12 are not.
models, and the SMD model, developed at the University of Minnesota.[Marenich et al.(2007)Marenich, Olson, Kelly, Cramer, and Truhlar, Marenich et al.(2013)Marenich, Cramer, and Truhlar, Marenich et al.(2009)Marenich, Olson, Kelly, Cramer, and Truhlar] SM8 and SM12 are based upon the generalized Born method for electrostatics, augmented with atomic surface tensions intended to capture non-electrostatic effects (cavitation, dispersion, exchange repulsion, and changes in solvent structure). Empirical corrections of this sort are also available for the PCMs mentioned above, but within SM8 and SM12 these parameters have been optimized to reproduce experimental solvation energies. SMD (where the “D” is for “density") combines IEF-PCM with the non-electrostatic corrections, but because the electrostatics is based on the density rather than atomic point charges, it is supported for arbitrary basis sets whereas SM8 and SM12 are not.
Model Cavity Non- Supported Construction Discretization Electrostatic Basis Terms? Sets Kirkwood-Onsager spherical point charges no all Langevin Dipoles atomic spheres dipoles in no all (user-definable) 3-d space C-PCM atomic spheres point charges or user- all (user-definable) smooth Gaussians specified SS(V)PE/ atomic spheres point charges or user- all IEF-PCM (user-definable) smooth Gaussians specified COSMO predefined point charges none all atomic spheres Isodensity SS(V)PE isodensity contour point charges none all SM8 predefined generalized automatic 6-31G* atomic spheres Born 6-31+G* 6-31+G** SM12 predefined generalized automatic all atomic spheres Born SMD predefined point charges automatic all atomic spheres
Table 12.1 summarizes the implicit solvent models that are available in Q-Chem. Solvent models are invoked via the SOLVENT_METHOD keyword, as shown below. Additional details about each particular solvent model can be found in the sections that follow. In general, these methods are available for any SCF level of electronic structure theory, though in the case of SM8 only certain basis sets are supported. Post-Hartree–Fock calculations can be performed by first running an SCF + PCM job, in which case the correlated wave function will employ MOs and Hartree-Fock energy levels that are polarized by the solvent.
Table 12.2 summarizes the analytical energy gradient and Hessian available with implicit solvent models. For unsupported methods, finite difference methods may be used for performing geometry optimizations and frequency calculations.
Energy Derivatives C-PCM SS(V)PE/ COSMO SM8 SM12 SMD IEF-PCM SCF energy gradient yes yes yes yes no yes SCF energy Hessian yes no yes no no no CIS/TDDFT energy gradient yes no — unsupported — CIS/TDDFT energy Hessian yes no — unsupported — MP2 & DH-DFT energy — unsupported — derivatives Coupled cluster methods — unsupported —
Note: The job-control format for specifying implicit solvent models changed significantly starting in Q-Chem version 4.2.1. This change was made in an attempt to simply and unify the input notation for a large number of different models.
SOLVENT_METHOD
Sets the preferred solvent method.
TYPE:
STRING
DEFAULT:
0
OPTIONS:
0
Do not use a solvation model.
ONSAGER
Use the Kirkwood-Onsager model (Section 12.2.1).
PCM
Use an apparent surface charge, polarizable continuum model
(Section 12.2.2).
ISOSVP
Use the isodensity implementation of the SS(V)PE model
(Section 12.2.5).
COSMO
Use COSMO (similar to C-PCM but with an outlying charge
correction;[Klamt and Jonas(1996), Baldridge and Klamt(1997)] see Section 12.2.7).
SM8
Use version 8 of the Cramer-Truhlar SM
model (Section 12.2.8.1).
SM12
Use version 12 of the SM
model (Section 12.2.8.2).
SMD
Use SMD (Section 12.2.8.3).
CHEM_SOL
Use the Langevin Dipoles model (Section 12.2.9).
RECOMMENDATION:
Consult the literature. PCM is a collective name for a family of models and additional input options may be required in this case, in order to fully specify the model. (See Section 12.2.2.) Several versions of SM12 are available as well, as discussed in Section 12.2.8.2.
Before going into detail about each of these models, a few potential points of confusion warrant mention, with regards to nomenclature. First, “PCM” refers to a family of models that includes C-PCM and SS(V)PE/IEF-PCM (the latter two being completely equivalent[Cancès and Mennucci(2001)]). One or the other of these models can be selected by additional job control variables in a $pcm input section, as described in Section 12.2.2. COSMO is very similar to C-PCM but includes a correction for that part of the solute’s electron density that penetrates beyond the cavity (the so-called “outlying charge”).[Klamt and Jonas(1996), Baldridge and Klamt(1997)] This is discussed in Section 12.2.7.
Two implementations of the SS(V)PE model are also available. The PCM implementation (which is requested by setting SOLVENT_METHOD = PCM) uses a solute cavity constructed from atom-centered spheres, as with most other PCMs. On the other hand, setting SOLVENT_METHOD = ISOSVP requests an SS(V)PE calculation in which the solute cavity is defined by an isocontour of the solute’s own electron density, as advocated by Chipman.[Chipman(2000), Chipman(2002), Chipman and Dupuis(2002)] This is an appealing, one-parameter cavity construction, although it is unclear that this construction alone is superior in its accuracy to carefully-parameterized atomic radii,[Barone et al.(1997)Barone, Cossi, and Tomasi] at least not without additional, non-electrostatic terms included,[Pomogaeva and Chipman(2011), Pomogaeva and Chipman(2013), Pomogaeva and Chipman(2014), Pomogaeva and Chipman(2015)] which are available in Q-Chem’s implementation of the isodensity version of SS(V)PE (Section 12.2.6). Moreover, analytic energy gradients are not available for the isodensity cavity construction, whereas they are available when the cavity is constructed from atom-centered spheres. One additional subtlety, which is discussed in detail in Ref. Lange:2011, is the fact that the PCM implementation of the equation for the SS(V)PE surface charges [Eq. eq:Kq=Rv] uses an asymmetric  matrix. In contrast, Chipman’s isodensity implementation uses a symmetrized
matrix. In contrast, Chipman’s isodensity implementation uses a symmetrized  matrix. Although the symmetrized version is somewhat more computationally efficient when the number of surface charges is large, the asymmetric version is better justified, theoretically.[Lange and Herbert(2011)] (This admittedly technical point is clarified in Section 12.2.2 and in particular in Table 12.3.)
matrix. Although the symmetrized version is somewhat more computationally efficient when the number of surface charges is large, the asymmetric version is better justified, theoretically.[Lange and Herbert(2011)] (This admittedly technical point is clarified in Section 12.2.2 and in particular in Table 12.3.)
Regarding the accuracy of these models for solvation free energies ( ), SM8 achieves sub-kcal/mol accuracy for neutral molecules, based on comparison to a large database of experimental values, although average errors for ions are more like 4 kcal/mol.[Cramer and Truhlar(2008)] To achieve comparable accuracy with IEF-PCM/SS(V)PE, non-electrostatic terms must be included.[Klamt et al.(2009)Klamt, Mennucci, Tomasi, Barone, Curutchet, Orozco, and Luque, Pomogaeva and Chipman(2011), Pomogaeva and Chipman(2014)] The SM12 model does not improve upon SM8 in any statistical sense,[Marenich et al.(2013)Marenich, Cramer, and Truhlar] but does lift one important restriction on the level of electronic structure that can be combined with these models. Specifically, the Generalized Born model used in SM8 is based on a variant of Mulliken-style atomic charges, and is therefore parameterized only for a few small basis sets, e.g., 6-31G*. SM12, on the other hand, uses a variety of charge schemes that are stable with respect to basis-set expansion, and can therefore be combined with any level of electronic structure theory for the solute. Like IEF-PCM, the SMD model is also applicable to any basis sets, and its accuracy is comparable to SM8 and SM12.[Marenich et al.(2009)Marenich, Olson, Kelly, Cramer, and Truhlar] Quantitative fluid-phase thermodynamics can also be obtained using Klamt’s COSMO-RS approach,[Klamt(1995), Klamt et al.(2010)Klamt, Eckert, and Arlt] where RS stands for “real solvent”. The COSMO-RS approach is not included in Q-Chem and requires the COSMOtherm program, which is licensed separately through COSMOlogic,[COS()] but Q-Chem can write the input files that are need by COSMOtherm.
), SM8 achieves sub-kcal/mol accuracy for neutral molecules, based on comparison to a large database of experimental values, although average errors for ions are more like 4 kcal/mol.[Cramer and Truhlar(2008)] To achieve comparable accuracy with IEF-PCM/SS(V)PE, non-electrostatic terms must be included.[Klamt et al.(2009)Klamt, Mennucci, Tomasi, Barone, Curutchet, Orozco, and Luque, Pomogaeva and Chipman(2011), Pomogaeva and Chipman(2014)] The SM12 model does not improve upon SM8 in any statistical sense,[Marenich et al.(2013)Marenich, Cramer, and Truhlar] but does lift one important restriction on the level of electronic structure that can be combined with these models. Specifically, the Generalized Born model used in SM8 is based on a variant of Mulliken-style atomic charges, and is therefore parameterized only for a few small basis sets, e.g., 6-31G*. SM12, on the other hand, uses a variety of charge schemes that are stable with respect to basis-set expansion, and can therefore be combined with any level of electronic structure theory for the solute. Like IEF-PCM, the SMD model is also applicable to any basis sets, and its accuracy is comparable to SM8 and SM12.[Marenich et al.(2009)Marenich, Olson, Kelly, Cramer, and Truhlar] Quantitative fluid-phase thermodynamics can also be obtained using Klamt’s COSMO-RS approach,[Klamt(1995), Klamt et al.(2010)Klamt, Eckert, and Arlt] where RS stands for “real solvent”. The COSMO-RS approach is not included in Q-Chem and requires the COSMOtherm program, which is licensed separately through COSMOlogic,[COS()] but Q-Chem can write the input files that are need by COSMOtherm.
The following sections provide more details regarding theory and job control for the various implicit solvent models that are available in Q-Chem. In addition, recent review articles are available for PCM methods,[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] SM ,[Cramer and Truhlar(2008)] and COSMO.[Klamt(2011)] Formal relationships between various PCMs have been discussed in Refs. Chipman:2002a,Lange:2011.
,[Cramer and Truhlar(2008)] and COSMO.[Klamt(2011)] Formal relationships between various PCMs have been discussed in Refs. Chipman:2002a,Lange:2011.
12.2.1 Kirkwood-Onsager Model
The simplest implicit solvation model available in Q-Chem is the Kirkwood-Onsager model,[Kirkwood(1934), Onsager(1936), Kirkwood(1939)] wherein the solute is placed inside of a spherical cavity that is surrounded by a homogeneous dielectric medium. This model is characterized by two parameters: the cavity radius,  , and the solvent dielectric constant,
, and the solvent dielectric constant,  . The former is typically calculated according to
. The former is typically calculated according to
 |
(12.1) |
where  is the solute’s molar volume, usually obtained from experiment (molecular weight or density[Weast(1989)]), and
is the solute’s molar volume, usually obtained from experiment (molecular weight or density[Weast(1989)]), and  is Avogadro’s number. It is also common to add 0.5 Å to the value of
is Avogadro’s number. It is also common to add 0.5 Å to the value of  in Eq. (12.1) in order to account for the first solvation shell.[Wong et al.(1991)Wong, Frisch, and Wiberg] Alternatively,
in Eq. (12.1) in order to account for the first solvation shell.[Wong et al.(1991)Wong, Frisch, and Wiberg] Alternatively,  is sometimes selected as the maximum distance between the solute center of mass and the solute atoms, plus the relevant van der Waals radii. A third option is to set
is sometimes selected as the maximum distance between the solute center of mass and the solute atoms, plus the relevant van der Waals radii. A third option is to set  (the cavity diameter) equal to the largest solute–solvent internuclear distance, plus the van der Waals radii of the relevant atoms. Unfortunately, solvation energies are typically quite sensitive to the choice of
(the cavity diameter) equal to the largest solute–solvent internuclear distance, plus the van der Waals radii of the relevant atoms. Unfortunately, solvation energies are typically quite sensitive to the choice of  (and to the construction of the solute cavity, more generally).
(and to the construction of the solute cavity, more generally).
Unlike older versions of the Kirkwood-Onsager model, in which the solute’s electron distribution was described entirely in terms of its dipole moment, Q-Chem’s version can use multipoles of arbitrarily high order, including the Born (monopole) term for charged solutes,[Born(1920)] in order to describe the solute’s electrostatic potential. The solute–continuum electrostatic interaction energy is then computed using analytic expressions for the interaction of the point multipoles with a dielectric continuum.
Energies and analytic gradients for the Kirkwood-Onsager solvent model are available for Hartree-Fock, DFT, and CCSD calculations. It is often advisable to perform a gas-phase calculation of the solute molecule first, which can serve as the initial guess for a subsequent Kirkwood-Onsager implicit solvent calculation.
The Kirkwood-Onsager SCRF is requested by setting SOLVENT_METHOD = ONSAGER in the $rem section (along with normal job control variables for an energy or gradient calculation), and furthermore specifying several additional options in a $solvent input section, as described below. Of these, the keyword CavityRadius is required. The $rem variable CC_SAVEAMPL may save some time for CCSD calculations using the Kirkwood-Onsager model.
Note: SCRF and CCSD combo works only in CCMAN (with CCMAN2 = FALSE).
Note: The following three job control variables belong only in the $solvent section. Do not place them in the $rem section. As with other parts of the Q-Chem input file, this input section is not case-sensitive.
CavityRadius
Sets the radius of the spherical solute cavity.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
No default.
OPTIONS:

Desired cavity radius, in Ångstroms.
RECOMMENDATION:
Use Eq. eq1000.
Dielectric
Sets the dielectric constant of the solvent continuum.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
78.39
OPTIONS:

Use a (dimensionless) value of
.
RECOMMENDATION:
As per required solvent; the default corresponds to water at 25
C.
MultipoleOrder
Determines the order to which the multipole expansion of the solute charge density is carried out.
INPUT SECTION: $solvent
TYPE:
INTEGER
DEFAULT:
15
OPTIONS:
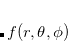
Include up to
th order multipoles.
RECOMMENDATION:
Use the default. The multipole expansion is usually converged by order
= 15.
Example 12.282 Onsager model applied at the Hartree-Fock level to H O in acetonitrile
O in acetonitrile
$molecule
0 1
O 0.00000000 0.00000000 0.11722303
H -0.75908339 0.00000000 -0.46889211
H 0.75908339 0.00000000 -0.46889211
$end
$rem
METHOD HF
BASIS 6-31g**
SOLVENT_METHOD Onsager
$end
$solvent
CavityRadius 1.8 ! 1.8 Angstrom Solute Radius
Dielectric 35.9 ! Acetonitrile
MultipoleOrder 15 ! this is the default value
$end
Example 12.283 Kirkwood-Onsager SCRF applied to hydrogen fluoride in water, performing a gas-phase calculation first.
$molecule
0 1
H 0.000000 0.000000 -0.862674
F 0.000000 0.000000 0.043813
$end
$rem
METHOD HF
BASIS 6-31G*
$end
@@@
$molecule
0 1
H 0.000000 0.000000 -0.862674
F 0.000000 0.000000 0.043813
$end
$rem
JOBTYPE FORCE
METHOD HF
BASIS 6-31G*
SOLVENT_METHOD ONSAGER
SCF_GUESS READ ! read vacuum solution as a guess
$end
$solvent
CavityRadius 2.5
$end
12.2.2 Polarizable Continuum Models
Clearly, the Kirkwood-Onsager model is inappropriate if the solute is very non-spherical. Nowadays, a more general class of “apparent surface charge” SCRF solvation models are much more popular, to the extent that the generic term “polarizable continuum model” (PCM) is typically used to denote these methods.[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] Apparent surface charge PCMs improve upon the Kirkwood-Onsager model in two ways. Most importantly, they provide a much more realistic description of molecular shape, typically by constructing the “solute cavity” (i.e., the interface between the atomistic region and the dielectric continuum) from a union of atom-centered spheres, an aspect of the model that is discussed in Section 12.2.2.2. In addition, the exact electron density of the solute (rather than a multipole expansion) is used to polarize the continuum. Electrostatic interactions between the solute and the continuum manifest as an induced charge density on the cavity surface, which is discretized into point charges for practical calculations. The surface charges are determined based upon the solute’s electrostatic potential at the cavity surface, hence the surface charges and the solute wave function must be determined self-consistently.
12.2.2.1 Formal Theory and Discussion of Different Models
The PCM literature has a long history[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] and there are several different models in widespread use; connections between these models have not always been appreciated.[Chipman(2000), Cancès and Mennucci(2001), Chipman(2002), Lange and Herbert(2011)] Chipman[Chipman(2000), Chipman(2002)] has shown how various PCMs can be formulated within a common theoretical framework; see Ref. Herbert:2016a for a pedagogical introduction. The PCM takes the form of a set of linear equations,
 |
(12.2) |
in which the induced charges  at the cavity surface discretization points [organized into a vector
at the cavity surface discretization points [organized into a vector  in Eq. eq:Kq=Rv] are computed from the values
in Eq. eq:Kq=Rv] are computed from the values  of the solute’s electrostatic potential at those same discretization points. The form of the matrices
of the solute’s electrostatic potential at those same discretization points. The form of the matrices  and
and  depends upon the particular PCM in question. These matrices are given in Table 12.3 for the PCMs that are available in Q-Chem.
depends upon the particular PCM in question. These matrices are given in Table 12.3 for the PCMs that are available in Q-Chem.
Model |
Literature |
Matrix |
Matrix |
Scalar |
Refs. |
||||
COSMO |
Klamt:1993 |
|
|
|
C-PCM |
Truong:1995,Barone:1998 |
|
|
|
IEF-PCM |
Chipman:2000,Cances:2001a |
|
|
|
SS(V)PE |
Chipman:2000,Chipman:2002b |
|
|
|
 consists of Coulomb interactions between the cavity charges and
consists of Coulomb interactions between the cavity charges and  is the discretized version of the matrix that generates the outward-pointing normal electric field vector. (See Refs. Chipman:2002a,Chipman:2002b,Herbert:2016a for detailed definitions.) The matrix
is the discretized version of the matrix that generates the outward-pointing normal electric field vector. (See Refs. Chipman:2002a,Chipman:2002b,Herbert:2016a for detailed definitions.) The matrix 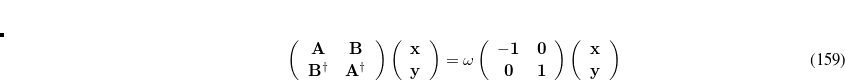 is diagonal and contains the surface areas of the cavity discretization elements, and
is diagonal and contains the surface areas of the cavity discretization elements, and  is a unit matrix. At the level of Eq. eq:Kq=Rv, COSMO and C-PCM differ only in the dielectric screening factor
is a unit matrix. At the level of Eq. eq:Kq=Rv, COSMO and C-PCM differ only in the dielectric screening factor  , although COSMO includes an additional outlying charge correction that goes beyond Eq. eq:Kq=Rv.[Klamt and Jonas(1996), Baldridge and Klamt(1997)]
, although COSMO includes an additional outlying charge correction that goes beyond Eq. eq:Kq=Rv.[Klamt and Jonas(1996), Baldridge and Klamt(1997)] The oldest PCM is the so-called D-PCM model of Tomasi and coworkers,[Miertuš et al.(1981)Miertuš, Scrocco, and Tomasi] but unlike the models listed in Table 12.3, D-PCM requires explicit evaluation of the electric field normal to the cavity surface, This is undesirable, as evaluation of the electric field is both more expensive and more prone to numerical problems as compared to evaluation of the electrostatic potential. Moreover, the dependence on the electric field can be formally eliminated at the level of the integral equation whose discretized form is given in Eq. eq:Kq=Rv.[Chipman(2000)] As such, D-PCM is essentially obsolete, and the PCMs available in Q-Chem require only the evaluation of the electrostatic potential, not the electric field.
The simplest PCM that continues to enjoy widespread use is the Conductor-Like Screening Model (COSMO) introduced by Klamt and Schüürmann.[Klamt and Schüürmann(1993)] Truong and Stefanovich[Truong and Stefanovich(1995)] later implemented the same model with a slightly different dielectric scaling factor ( in Table 12.3), and called this modification GCOSMO. The latter was implemented within the PCM formalism by Barone and Cossi et al.,[Barone and Cossi(1998), Cossi et al.(2003)Cossi, Rega, Scalmani, and Barone] who called the model C-PCM (for “conductor-like” PCM). In each case, the dielectric screening factor has the form
in Table 12.3), and called this modification GCOSMO. The latter was implemented within the PCM formalism by Barone and Cossi et al.,[Barone and Cossi(1998), Cossi et al.(2003)Cossi, Rega, Scalmani, and Barone] who called the model C-PCM (for “conductor-like” PCM). In each case, the dielectric screening factor has the form
 |
(12.3) |
where Klamt and Schüürmann proposed  but
but  was used in GCOSMO and C-PCM. The latter value is the correct choice for a single charge in a spherical cavity (i.e., the Born ion model), although Klamt and coworkers suggest that
was used in GCOSMO and C-PCM. The latter value is the correct choice for a single charge in a spherical cavity (i.e., the Born ion model), although Klamt and coworkers suggest that  is a better compromise, given that the Kirkwood-Onsager analytical result is
is a better compromise, given that the Kirkwood-Onsager analytical result is  for an
for an 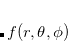 th-order multipole centered in a spherical cavity.[Klamt and Schüürmann(1993), Baldridge and Klamt(1997)] The distinction is irrelevant in high-dielectric solvents; the
th-order multipole centered in a spherical cavity.[Klamt and Schüürmann(1993), Baldridge and Klamt(1997)] The distinction is irrelevant in high-dielectric solvents; the  and
and  values of
values of  differ by only 0.6% for water at 25
differ by only 0.6% for water at 25 C, for example. Truong[Truong and Stefanovich(1995)] argues that
C, for example. Truong[Truong and Stefanovich(1995)] argues that  does a better job of preserving Gauss’ Law in low-dielectric solvents, but more accurate solvation energies (at least for neutral molecules, as compared to experiment) are sometimes obtained using
does a better job of preserving Gauss’ Law in low-dielectric solvents, but more accurate solvation energies (at least for neutral molecules, as compared to experiment) are sometimes obtained using  (Ref. Barone:1998). This result is likely highly sensitive to cavity construction, and in any case, both versions are available in Q-Chem.
(Ref. Barone:1998). This result is likely highly sensitive to cavity construction, and in any case, both versions are available in Q-Chem.
Whereas the original COSMO model introduced by Klamt and Schüürmann[Klamt and Schüürmann(1993)] corresponds to Eq. eq:Kq=Rv with  and
and  as defined in Table 12.3, Klamt and coworkers later introduced a correction for outlying charge that goes beyond Eq. eq:Kq=Rv.[Klamt and Jonas(1996), Baldridge and Klamt(1997)] Klamt now consistently refers to this updated model as “COSMO”,[Klamt(2011)] and we shall adopt this nomenclature as well. COSMO, with the outlying charge correction, is available in Q-Chem and is described in Section 12.2.7. In contrast, C-PCM consists entirely of Eq. eq:Kq=Rv with matrices
as defined in Table 12.3, Klamt and coworkers later introduced a correction for outlying charge that goes beyond Eq. eq:Kq=Rv.[Klamt and Jonas(1996), Baldridge and Klamt(1997)] Klamt now consistently refers to this updated model as “COSMO”,[Klamt(2011)] and we shall adopt this nomenclature as well. COSMO, with the outlying charge correction, is available in Q-Chem and is described in Section 12.2.7. In contrast, C-PCM consists entirely of Eq. eq:Kq=Rv with matrices  and
and  as defined in Table 12.3, although it is possible to modify the dielectric screening factor to use the
as defined in Table 12.3, although it is possible to modify the dielectric screening factor to use the  value (as in COSMO) rather than the
value (as in COSMO) rather than the  value. Additional non-electrostatic terms can be added at the user’s discretion, as discussed below, but there is no explicit outlying charge correction in C-PCM. These and other fine-tuning details for PCM jobs are controllable via the $pcm input section that is described in Section 12.2.3.
value. Additional non-electrostatic terms can be added at the user’s discretion, as discussed below, but there is no explicit outlying charge correction in C-PCM. These and other fine-tuning details for PCM jobs are controllable via the $pcm input section that is described in Section 12.2.3.
As compared to C-PCM, a more sophisticated treatment of continuum electrostatic interactions is afforded by the “surface and simulation of volume polarization for electrostatics” [SS(V)PE] approach.[Chipman(2000)] Formally speaking, this model provides an exact treatment of the surface polarization (i.e., the surface charge induced by the solute charge that is contained within the solute cavity, which induces a surface polarization owing to the discontinuous change in dielectric constant across the cavity boundary) but also an approximate treatment of the volume polarization (arising from the aforementioned outlying charge). The “SS(V)PE” terminology is Chipman’s notation,[Chipman(2000)] but this model is formally equivalent, at the level of integral equations, to the “integral equation formalism” (IEF-PCM) that was developed originally by Cancès et al..[Cancès(1997), Tomasi et al.(1999)Tomasi, Mennucci, and Cancès] Some difference do arise when the integral equations are discretized to form finite-dimensional matrix equations,[Lange and Herbert(2011)] and it should be noted from Table 12.3 that SS(V)PE uses a symmetrized form of the  matrix as compared to IEF-PCM. The asymmetric IEF-PCM is the recommended approach,[Lange and Herbert(2011)] although only the symmetrized version is available in the isodensity implementation of SS(V)PE that is discussed in Section 12.2.5. As with the obsolete D-PCM approach, the original version of IEF-PCM explicitly required evaluation of the normal electric field at the cavity surface, but it was later shown that this dependence could be eliminated to afford the version described in Table 12.3.[Chipman(2000), Cancès and Mennucci(2001)] This version requires only the electrostatic potential, and is thus preferred, and it is this version that we designate as IEF-PCM. The C-PCM model becomes equivalent to SS(V)PE in the limit
matrix as compared to IEF-PCM. The asymmetric IEF-PCM is the recommended approach,[Lange and Herbert(2011)] although only the symmetrized version is available in the isodensity implementation of SS(V)PE that is discussed in Section 12.2.5. As with the obsolete D-PCM approach, the original version of IEF-PCM explicitly required evaluation of the normal electric field at the cavity surface, but it was later shown that this dependence could be eliminated to afford the version described in Table 12.3.[Chipman(2000), Cancès and Mennucci(2001)] This version requires only the electrostatic potential, and is thus preferred, and it is this version that we designate as IEF-PCM. The C-PCM model becomes equivalent to SS(V)PE in the limit  ,[Chipman(2000), Lange and Herbert(2011)] which means that C-PCM must somehow include an implicit correction for volume polarization, even if this was not by design.[Klamt and Jonas(1996)] For
,[Chipman(2000), Lange and Herbert(2011)] which means that C-PCM must somehow include an implicit correction for volume polarization, even if this was not by design.[Klamt and Jonas(1996)] For  , numerical calculations reveal that there is essentially no difference between SS(V)PE and C-PCM results.[Lange and Herbert(2011)] Since C-PCM is less computationally involved as compared to SS(V)PE, it is the PCM of choice in high-dielectric solvents. The computational savings relative to SS(V)PE may be particularly significant for large QM/MM/PCM jobs. For a more detailed discussion of the history of these models, see the lengthy and comprehensive review by Tomasi et al..[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] For a briefer discussion of the connections between these models, see Refs. Chipman:2002a,Lange:2011,Herbert:2016a.
, numerical calculations reveal that there is essentially no difference between SS(V)PE and C-PCM results.[Lange and Herbert(2011)] Since C-PCM is less computationally involved as compared to SS(V)PE, it is the PCM of choice in high-dielectric solvents. The computational savings relative to SS(V)PE may be particularly significant for large QM/MM/PCM jobs. For a more detailed discussion of the history of these models, see the lengthy and comprehensive review by Tomasi et al..[Tomasi et al.(2005)Tomasi, Mennucci, and Cammi] For a briefer discussion of the connections between these models, see Refs. Chipman:2002a,Lange:2011,Herbert:2016a.
12.2.2.2 Cavity Construction and Discretization

Construction of the cavity surface is a crucial aspect of PCMs, as computed properties are quite sensitive to the details of the cavity construction. Most cavity constructions are based on a union of atom-centered spheres (see Fig. 12.1), but there are yet several different constructions whose nomenclature is occasionally confused in the literature. Simplest and most common is the van der Waals (vdW) surface consisting of a union of atom-centered spheres. Traditionally,[Bonaccorsi et al.(1984)Bonaccorsi, Palla, and Tomasi, Tomasi and Persico(1994)] and by default in Q-Chem, the atomic radii are taken to be 1.2 times larger than vdW radii extracted from crystallographic data, originally by Bondi (and thus sometimes called “Bondi radii”).[Bondi(1964)] This 20% augmentation is intended to mimic the fact that solvent molecules cannot approach all the way to the vdW radius of the solute atoms, though it’s not altogether clear that this is an optimal value. (The default scaling factor in Q-Chem is 1.2 but can be modified by the user.) An alternative to scaling the atomic radii is to add a certain fixed increment to each, representing the approximate size of a solvent molecule (e.g., 1.4 Å for water) and leading to what is known as the solvent accessible surface (SAS). From another point of view, the SAS represents the surface defined by the center of a spherical solvent molecule as it rolls over the vdW surface, as suggested in Fig. 12.1. Both the vdW surface and the SAS possess cusps where the atomic spheres intersect, although these become less pronounced as the atomic radii are scaled or augmented. These cusps are eliminated in what is known as the solvent-accessible surface (SES), sometimes called the Connolly surface or the “molecular surface". The SES uses the surface of the probe sphere at points where it is simultaneously tangent to two or more atomic spheres to define elements of a “re-entrant surface” that smoothly connects the atomic (or “contact”) surface.[Lange et al.()Lange, Herbert, Albrecht, and Herbert]
Having chosen a model for the cavity surface, this surface is discretized using atom-centered Lebedev grids[Lebedev(1976), Lebedev(1977), Lebedev and Laikov(1999)] of the same sort that are used to perform the numerical integrations in DFT. (Discretization of the re-entrant facets of the SES is somewhat more complicated but similar in spirit.[Lange et al.()Lange, Herbert, Albrecht, and Herbert]) Surface charges  are located at these grid points and the Lebedev quadrature weights can be used to define the surface area associated with each discretization point.[Lange and Herbert(2010a)]
are located at these grid points and the Lebedev quadrature weights can be used to define the surface area associated with each discretization point.[Lange and Herbert(2010a)]
A long-standing (though not well-publicized) problem with the aforementioned discretization procedure is that it fails to afford continuous potential energy surfaces as the solute atoms are displaced, because certain surface grid points may emerge from, or disappear within, the solute cavity, as the atomic spheres that define the cavity are moved. This undesirable behavior can inhibit convergence of geometry optimizations and, in certain cases, lead to very large errors in vibrational frequency calculations.[Lange and Herbert(2010a)] It is also a fundamental hindrance to molecular dynamics calculations.[Lange and Herbert(2010b)] Building upon earlier work by York and Karplus,[York and Karplus(1999)] Lange and Herbert[Lange and Herbert(2010a), Lange and Herbert(2010b), Lange et al.()Lange, Herbert, Albrecht, and Herbert] developed a general scheme for implementing apparent surface charge PCMs in a manner that affords smooth potential energy surfaces, even for ab initio molecular dynamics simulations involving bond breaking.[Lange and Herbert(2010b), Herbert and Lange(2016)] Notably, this approach is faithful to the properties of the underlying integral equation theory on which the PCMs are based, in the sense that the smoothing procedure does not significantly perturb solvation energies or cavity surface areas.[Lange and Herbert(2010a), Lange and Herbert(2010b)] The smooth discretization procedure combines a switching function with Gaussian blurring of the cavity surface charge density, and is thus known as the “Switching/Gaussian” (SWIG) implementation of the PCM.
Both single-point energies and analytic energy gradients are available for SWIG PCMs, when the solute is described using molecular mechanics or an SCF (Hartree-Fock or DFT) electronic structure model, except that for the SES cavity model only single-point energies are available. Analytic Hessians are available for the C-PCM model only. (As usual, vibrational frequencies for other models will be computed, if requested, by finite difference of analytic energy gradients.) Single-point energy calculations using correlated wave functions can be performed in conjunction with these solvent models, in which case the correlated wave function calculation will use Hartree-Fock molecular orbitals that are polarized in the presence of the continuum dielectric solvent (i.e., there is no post-Hartree–Fock PCM correction).
Researchers who use these PCMs are asked to cite Refs. Lange:2010b,Lange:2011, which provide the details of Q-Chem’s implementation, and Ref. Lange:2018 if the SES is used. (We point the reader in particular to Ref. Lange:2010b, which provides an assessment of the discretization errors that can be anticipated using various PCMs and Lebedev grids; default grid values in Q-Chem were established based on these tests.) When publishing results based on PCM calculations, it is essential to specify both the precise model that is used (see Table 12.3) as well as how the cavity was constructed.
For example, “Bondi radii multiplied by 1.2”, which is the Q-Chem default, except for hydrogen, where the factor is reduced to 1.1,[Rowland and Taylor(1996)] as per usual. Radii for main-group elements that were not provided by Bondi are taken from Ref. Mantina:2009. Absent details such as these, PCM calculations will be difficult to reproduce in other electronic structure programs.
12.2.2.3 Nonequilibrium Solvation for Vertical Excitation, Ionization and Emission
In vertical excitation or ionization, the solute undergoes a sudden change in its charge distribution. Various microscopic motions of the solvent have characteristic times to reach certain polarization response, and fast part of the solvent response (electrons) can follow such a dynamic process while the remaining degrees of freedom (nuclei) remain unchanged as in the initial state. Such splitting of the solvent response gives rise to nonequilibrium solvation. In the literature, two different approaches have been developed for describing nonequilibrium solvent effects: the linear response (LR) approach[Cammi and Mennucci(1999), Cossi and Barone(2001)] and the state-specific (SS) approach.[Tomasi and Persico(1994), Cammi and Tomasi(1995), Cossi and Barone(2000), Improta et al.(2006)Improta, Barone, Scalmani, and Frisch] Both are implemented in Q-Chem,[You et al.(2015)You, Mewes, Dreuw, and Herbert],at the SCF level for vertical ionization and at the corresponding level (CIS, TDDFT or ADC, see Section 7.8.7) for vertical excitation. A brief introduction to these methods is given below, and users of the nonequilibrium PCM features are asked to cite Refs. You:2015 and Mewes:2015a. State-specific solvent-field equilibration for long-lived excited states to compute e.g. emission energies is implemented for the ADC-suite of methods as described in section 7.8.7. Users of this equilibrium-solvation PCM please cite and be referred to Ref. Mewes:2017.
The LR approach considers the solvation effects as a coupling between a pair of transitions, one for solute and the other for solvent. The transition frequencies when the interaction between the solute and solvent is turned on may be determined by considering such an interaction as a perturbation. In the framework of TDDFT, the solvent/solute interaction is given by[Hsu et al.(2001)Hsu, Fleming, Head-Gordon, and Head-Gordon]
 |
(12.4) |
where 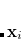 is the charge density response function of the solvent and
is the charge density response function of the solvent and  is the solute’s transition density. This term accounts for a dynamical correction to the transition energy so that it is related to the response of the solvent to the charge density of the solute oscillating at the solute transition frequency (
is the solute’s transition density. This term accounts for a dynamical correction to the transition energy so that it is related to the response of the solvent to the charge density of the solute oscillating at the solute transition frequency (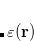 ). Within a PCM, only classical Coulomb interactions are taken into account, and Eq. eq:LR-term becomes
). Within a PCM, only classical Coulomb interactions are taken into account, and Eq. eq:LR-term becomes
 |
(12.7) |
where  is PCM solvent response operator for a generic dielectric constant,
is PCM solvent response operator for a generic dielectric constant,  . The integral of
. The integral of  and the potential of the density
and the potential of the density  gives the surface charge density for the solvent polarization.
gives the surface charge density for the solvent polarization.
The state-specific (SS) approach takes into account the capability of a part of the solvent degrees of freedom to respond instantaneously to changes in the solute wave function upon excitation. Such an effect is not accounted for in the LR approach. In SS, a generic solvated-solute excited state  is obtained as a solution of a nonlinear Schrödinger equation
is obtained as a solution of a nonlinear Schrödinger equation
 |
(12.9) |
that depends upon the solute’s charge distribution. Here  is the usual Hamiltonian for the solute in vacuum and the reaction field operator
is the usual Hamiltonian for the solute in vacuum and the reaction field operator  generates the electrostatic potential of the apparent surface charge density (Section 12.2.2.1), corresponding to slow and fast polarization response. The solute is polarized self-consistently with respect to the solvent’s reaction field. In case of vertical ionization rather than excitation, both the ionized and non-ionized states can be treated within a ground-state formalism. For vertical excitations, self-consistent SS models have been developed for various excited-state methods,[Improta et al.(2006)Improta, Barone, Scalmani, and Frisch, Marenich et al.(2011)Marenich, Cramer, Truhlar, Guido, Mennucci, Scalmani, and Frisch] including both CIS and TDDFT.
generates the electrostatic potential of the apparent surface charge density (Section 12.2.2.1), corresponding to slow and fast polarization response. The solute is polarized self-consistently with respect to the solvent’s reaction field. In case of vertical ionization rather than excitation, both the ionized and non-ionized states can be treated within a ground-state formalism. For vertical excitations, self-consistent SS models have been developed for various excited-state methods,[Improta et al.(2006)Improta, Barone, Scalmani, and Frisch, Marenich et al.(2011)Marenich, Cramer, Truhlar, Guido, Mennucci, Scalmani, and Frisch] including both CIS and TDDFT.
In a linear dielectric medium, the solvent polarization is governed by the electric susceptibility, ![$\chi = [\varepsilon (\omega ) - 1]/4\pi $](images/img-1975.png) , where
, where  is the frequency-dependent permittivity, In case of very fast vertical transitions, the dielectric response is ruled by the optical dielectric constant,
is the frequency-dependent permittivity, In case of very fast vertical transitions, the dielectric response is ruled by the optical dielectric constant,  , where
, where  is the solvent’s index of refraction. In both LR and SS, the fast part of the solvent’s degrees of freedom is in equilibrium with the solute density change. Within PCM, the fast solvent polarization charges for the SS excited state
is the solvent’s index of refraction. In both LR and SS, the fast part of the solvent’s degrees of freedom is in equilibrium with the solute density change. Within PCM, the fast solvent polarization charges for the SS excited state  can be obtained by solving the following equation:[Cossi and Barone(2000)]
can be obtained by solving the following equation:[Cossi and Barone(2000)]
![\begin{equation} \label{eq:Kq=Rv-fast} \ensuremath{\mathbf{K}}_{\varepsilon _{\ensuremath{\mathrm{opt}}}} \ensuremath{\mathbf{q}}^{\ensuremath{\mathrm{fast,SS}}}_ i = \ensuremath{\mathbf{R}}_{\varepsilon _{\ensuremath{\mathrm{opt}}}}\left[\ensuremath{\mathbf{v}}_ i + \ensuremath{\mathbf{v}}(\ensuremath{\mathbf{q}}^{\ensuremath{\mathrm{slow}}}_0)\right] \; . \end{equation}](images/img-1978.png) |
(12.10) |
Here  is the discretized fast surface charge. The dielectric constants in the matrices
is the discretized fast surface charge. The dielectric constants in the matrices  and
and  (Section 12.2.2.1) are replaced with the optical dielectric constant, and
(Section 12.2.2.1) are replaced with the optical dielectric constant, and  is the potential of the solute’s excited state density,
is the potential of the solute’s excited state density,  . The quantity
. The quantity  is the potential of the slow part of the apparent surface charges in the ground state, which are given by
is the potential of the slow part of the apparent surface charges in the ground state, which are given by
 |
(12.11) |
For LR-PCM, the solvent polarization is subjected to the first-order changes to the electron density (TDDFT linear density response), and thus Eq. eq:Kq=Rv-fast becomes
 |
(12.12) |
The LR approach for CIS/TDDFT excitations and the self-consistent SS method (using the ground-state SCF) for vertical ionizations are available in Q-Chem. The self-consistent SS method for vertical excitations is not available, because this method is problematic in the vicinity of (near-) degeneracies between excited states, such as in the vicinity of a conical intersection. The fundamental problem in the SS approach is that each wave function  is an eigenfunction of a different Hamiltonian, since Eq. eq:SS-sdeq depend upon the specific state of interest. To avoid the ordering and the non-orthogonality problems, we compute the vertical excitation energy using a first-order, perturbative approximation to the SS approach,[Cammi et al.(2005)Cammi, Corni, Mennucci, and Tomasi, Caricato et al.(2006)Caricato, Mennucci, Tomasi, Ingrosso, Cammi, Corni, and Scalmani] in what we have termed the “ptSS” method.[Mewes et al.(2015a)Mewes, You, Wormit, Kriesche, Herbert, and Dreuw] The zeroth-order excited-state wave function can be calculated using various excited-state methods (currently available for CIS and TDDFT in Q-Chem) with solvent-relaxed molecular orbitals obtained from a ground-state PCM calculation. As mentioned previously, LR and SS describe different solvent relaxation features in nonequilibrium solvation. In the perturbation scheme, we can calculate the LR contribution using the zeroth-order transition density, in what we have called the "ptLR" approach. The combination of ptSS and ptLR yields quantitatively good solvatochromatic shifts in combination with TDDFT but not with the correlated variants of ADC, for which the pure ptSS approach was shown to be superior.[You et al.(2015)You, Mewes, Dreuw, and Herbert, Mewes et al.(2015a)Mewes, You, Wormit, Kriesche, Herbert, and Dreuw]
is an eigenfunction of a different Hamiltonian, since Eq. eq:SS-sdeq depend upon the specific state of interest. To avoid the ordering and the non-orthogonality problems, we compute the vertical excitation energy using a first-order, perturbative approximation to the SS approach,[Cammi et al.(2005)Cammi, Corni, Mennucci, and Tomasi, Caricato et al.(2006)Caricato, Mennucci, Tomasi, Ingrosso, Cammi, Corni, and Scalmani] in what we have termed the “ptSS” method.[Mewes et al.(2015a)Mewes, You, Wormit, Kriesche, Herbert, and Dreuw] The zeroth-order excited-state wave function can be calculated using various excited-state methods (currently available for CIS and TDDFT in Q-Chem) with solvent-relaxed molecular orbitals obtained from a ground-state PCM calculation. As mentioned previously, LR and SS describe different solvent relaxation features in nonequilibrium solvation. In the perturbation scheme, we can calculate the LR contribution using the zeroth-order transition density, in what we have called the "ptLR" approach. The combination of ptSS and ptLR yields quantitatively good solvatochromatic shifts in combination with TDDFT but not with the correlated variants of ADC, for which the pure ptSS approach was shown to be superior.[You et al.(2015)You, Mewes, Dreuw, and Herbert, Mewes et al.(2015a)Mewes, You, Wormit, Kriesche, Herbert, and Dreuw]
The LR and SS approaches can also be used in the study of photon emission processes.[Improta et al.(2007)Improta, Scalmani, Frisch, and Barone] An emission process can be treated as a vertical excitation at a stationary point on the excited-state potential surface. The basic requirement therefore is to prepare the solvent-relaxed geometry for the excited-state of interest. TDDFT/C-PCM analytic gradients and Hessian are available.
Section 7.3.5 for computational details regarding excited-state geometry optimization with PCM. An emission process is slightly more complicated than the absorption case. Two scenarios are discussed in literature, depending on the lifetime of an excited state in question. In the limiting case of ultra-fast excited state decay, when only fast solvent degrees of freedom are expected to be equilibrated with the excited-state density. In this limit, the emission energy can be computed exactly in the same way as the vertical excitation energy. In this case, excited state geometry optimization should be performed in the nonequilibrium limit. The other limit is that of long-lived excited state, e.g., strongly fluorescent species and phosphorescence. In the long-lived case, excited state geometry optimization should be performed with the solvent equilibrium limit. Thus, the excited state should be computed using an equilibrium LR or SS approach, and the ground state is calculated using nonequilibrium self-consistent SS approach. The latter approach is implemented for the ADC-based methods as described in Section 7.8.7.
12.2.3 PCM Job Control
A PCM calculation is requested by setting SOLVENT_METHOD = PCM in the $rem section. As mentioned above, there are a variety of different theoretical models that fall within the PCM family, so additional fine-tuning may be required, as described below.
12.2.3.1 $pcm section
Most PCM job control is accomplished via options specified in the $pcm input section, which allows the user to specify which flavor of PCM will be used, which algorithm will be used to solve the PCM equations, and other options. The format of the $pcm section is analogous to that of the $rem section:
$pcm
<Keyword> <parameter/option>
$end
Note: The following job control variables belong only in the $pcm section. Do not place them in the $rem section.
Theory
Specifies the which polarizable continuum model will be used.
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
CPCM
OPTIONS:
CPCM
Conductor-like PCM with
.
COSMO
Original conductor-like screening model with
.
IEFPCM
IEF-PCM with an asymmetric
matrix.
SSVPE
SS(V)PE model, equivalent to IEF-PCM with a symmetric
matrix.
RECOMMENDATION:
The IEF-PCM/SS(V)PE model is more sophisticated model than either C-PCM or COSMO, and probably more appropriate for low-dielectric solvents, but it is also more computationally demanding. In high-dielectric solvents there is little difference between these models. Note that the keyword COSMO in this context simply affects the dielectric screening factor
; to obtain the outlying charge correction suggested by Klamt,[Klamt and Jonas(1996), Baldridge and Klamt(1997)] one should use SOLVENT_METHOD = COSMO rather than SOLVENT_METHOD = PCM. (See Section 12.2.7.)
Method
Specifies which surface discretization method will be used.
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
SWIG
OPTIONS:
SWIG
Switching/Gaussian method
ISWIG
“Improved” Switching/Gaussian method with an alternative switching function
Spherical
Use a single, fixed sphere for the cavity surface.
Fixed
Use discretization point charges instead of smooth Gaussians.
RECOMMENDATION:
Use of SWIG is recommended only because it is slightly more efficient than the switching function of ISWIG. On the other hand, ISWIG offers some conceptually more appealing features and may be superior in certain cases. Consult Refs. Lange:2010b,Lange:2011 for a discussion of these differences. The Fixed option uses the Variable Tesserae Number (VTN) algorithm of Li and Jensen,[Li and Jensen(2004)] with Lebedev grid points. VTN uses point charges with no switching function or Gaussian blurring, and is therefore subject to discontinuities in geometry optimizations. It is not recommended, except to make contact with other calculations in the literature.
SwitchThresh
Threshold for discarding grid points on the cavity surface.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
8
OPTIONS:

Discard grid points when the switching function is less than
.
RECOMMENDATION:
Use the default, which is found to avoid discontinuities within machine precision. Increasing
reduces the cost of PCM calculations but can introduce discontinuities in the potential energy surface.
Construction of the solute cavity is an important part of the model and users should consult the literature in this capacity, especially with regard to the radii used for the atomic spheres. The default values provided in Q-Chem correspond to the consensus choice that has emerged over several decades, namely, to use vdW radii scaled by a factor of 1.2. The most widely-used set of vdW radii are those determined from crystallographic data by Bondi,[Bondi(1964)] although the radius for hydrogen was later adjusted to 1.1 Å,[Rowland and Taylor(1996)] and radii for those main-group elements not addressed by Bondi were provided later.[Mantina et al.(2009)Mantina, Chamberlin, Valero, Cramer, and Truhlar] This extended set of vdW is used by default in Q-Chem, and for simplicity we call these “Bondi radii” regardless of whether they come from Bondi’s original paper or the later work. Alternatively, atomic radii from the Universal Force Field (UFF) are available.[Rappé et al.(1992)Rappé, Casewit, Colwell, Goddard III, and Skiff] The main appeal of UFF radii is that they are defined for all atoms of the periodic table, though the quality of these radii for PCM applications is unclear. Finally, the user may specify his or her own radii for cavity construction using a $van_der_waals input section, the format for which is described in Section 12.2.9. No scaling factor is applied to user-defined radii. Note that  is allowed for a particular atomic radius, in which case the atom in question is not used to construct the cavity surface. This feature facilitates the construction of “united atom” cavities,[Barone et al.(1997)Barone, Cossi, and Tomasi] in which the hydrogen atoms do not get their own spheres and the heavy-atom radii are increased to compensate Finally, since the solvent molecules should not be able to penetrate all the way to the atomic vdW radii of the solute, it is traditional either to scale the atomic radii (vdW surface construction) or else to augment them with an assumed radius of a spherical solvent molecule (SAS construction), but not both.
is allowed for a particular atomic radius, in which case the atom in question is not used to construct the cavity surface. This feature facilitates the construction of “united atom” cavities,[Barone et al.(1997)Barone, Cossi, and Tomasi] in which the hydrogen atoms do not get their own spheres and the heavy-atom radii are increased to compensate Finally, since the solvent molecules should not be able to penetrate all the way to the atomic vdW radii of the solute, it is traditional either to scale the atomic radii (vdW surface construction) or else to augment them with an assumed radius of a spherical solvent molecule (SAS construction), but not both.
Radii
Specifies which set of atomic van der Waals radii will be used to define the solute cavity.
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
BONDI
OPTIONS:
BONDI
Use the (extended) set of Bondi radii.
FF
Use Lennard-Jones radii from a molecular mechanics force field.
UFF
Use radii form the Universal Force Field.
READ
Read the atomic radii from a $van_der_waals input section.
RECOMMENDATION:
Bondi radii are widely used. The FF option requires the user to specify an MM force field using the FORCE_FIELD $rem variable, and also to define the atom types in the $molecule section (see Section 12.3). This is not required for UFF radii.
vdwScale
Scaling factor for the atomic van der Waals radii used to define the solute cavity.
INPUT SECTION: $pcm
TYPE:
FLOAT
DEFAULT:
1.2
OPTIONS:
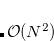
Use a scaling factor of
.
RECOMMENDATION:
The default value is widely used in PCM calculations, although a value of 1.0 might be appropriate if using a solvent-accessible surface.
SASradius
Form a “solvent accessible” surface with the given solvent probe radius.
INPUT SECTION: $pcm
TYPE:
FLOAT
DEFAULT:
0.0
OPTIONS:
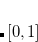
Use a solvent probe radius of
, in Å.
RECOMMENDATION:
The solvent probe radius is added to the scaled van der Waals radii of the solute atoms. A common solvent probe radius for water is 1.4 Å, but the user should consult the literature regarding the use of solvent-accessible surfaces.
SurfaceType
Selects the solute cavity surface construction.
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
VDW_SAS
OPTIONS:
VDW_SAS
van der Waals or solvent-accessible surface
SES
solvent-excluded surface
RECOMMENDATION:
The vdW surface and the SAS are each comprised simply of atomic spheres and thus share a common option; the only difference is the specification of a solvent probe radius, SASradius. For a true vdW surface, the probe radius should be zero (which is the default), whereas for the SAS the atomic radii are traditionally not scaled, hence vdwScale should be set to zero (which is not the default). For the SES, only SWIG discretization is available, but this can be used with any set of (scaled or unscaled) atomic radii, or with radii that are augmented by SASradius.
Historically, discretization of the cavity surface has involved “tessellation” methods that divide the cavity surface area into finite polygonal “tesserae”. (The GEPOL algorithm[Pascual-Ahuir et al.(1994)Pascual-Ahuir, Silla, and non] is perhaps the most widely-used tessellation scheme.) Tessellation methods, however, suffer not only from discontinuities in the cavity surface area and solvation energy as a function of the nuclear coordinates, but in addition they lead to analytic energy gradients that are complicated to derive and implement. To avoid these problems, Q-Chem’s SWIG PCM implementation[Lange and Herbert(2010a), Lange and Herbert(2010b), Lange and Herbert(2011)] uses Lebedev grids to discretize the atomic spheres. These are atom-centered grids with icosahedral symmetry, and may consist of anywhere from 26 to 5294 grid points per atomic sphere. The default values used by Q-Chem were selected based on extensive numerical tests.[Lange and Herbert(2010b), Lange and Herbert(2011)] The default for MM atoms (in MM/PCM or QM/MM/PCM jobs) is  Lebedev points per atomic sphere, whereas the default for QM atoms is
Lebedev points per atomic sphere, whereas the default for QM atoms is  . (This represents a change relative to Q-Chem versions earlier than 4.2.1, where the default for QM atoms was
. (This represents a change relative to Q-Chem versions earlier than 4.2.1, where the default for QM atoms was  .) These default values exhibit good rotational invariance and absolute solvation energies that, in most cases, lie within
.) These default values exhibit good rotational invariance and absolute solvation energies that, in most cases, lie within  0.5–1.0 kcal/mol of the
0.5–1.0 kcal/mol of the  limit,[Lange and Herbert(2010b)] although exceptions (especially where charged solutes are involved) can be found.[Lange and Herbert(2011)]
limit,[Lange and Herbert(2010b)] although exceptions (especially where charged solutes are involved) can be found.[Lange and Herbert(2011)]
Note: The acceptable values for the number of Lebedev points per sphere are  , 50, 110, 194, 302, 434, 590, 770, 974, 1202, 1454, 1730, 2030, 2354, 2702, 3074, 3470, 3890, 4334, 4802, or 5294.
, 50, 110, 194, 302, 434, 590, 770, 974, 1202, 1454, 1730, 2030, 2354, 2702, 3074, 3470, 3890, 4334, 4802, or 5294.
HPoints
The number of Lebedev grid points to be placed on H atoms in the QM system.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
302
OPTIONS:
Acceptable values are listed above.
RECOMMENDATION:
Use the default for geometry optimizations. For absolute solvation energies, the user may want to examine convergence with respect to
.
HeavyPoints
The number of Lebedev grid points to be placed non-hydrogen atoms in the QM system.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
302
OPTIONS:
Acceptable values are listed above.
RECOMMENDATION:
Use the default for geometry optimizations. For absolute solvation energies, the user may want to examine convergence with respect to
.
MMHPoints
The number of Lebedev grid points to be placed on H atoms in the MM subsystem.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
110
OPTIONS:
Acceptable values are listed above.
RECOMMENDATION:
Use the default for geometry optimizations. For absolute solvation energies, the user may want to examine convergence with respect to
. This option applies only to MM/PCM or QM/MM/PCM calculations.
MMHeavyPoints
The number of Lebedev grid points to be placed on non-hydrogen atoms in the MM subsystem.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
110
OPTIONS:
Acceptable values are listed above.
RECOMMENDATION:
Use the default for geometry optimizations. For absolute solvation energies, the user may want to examine convergence with respect to
. This option applies only to MM/PCM or QM/MM/PCM calculations.
Especially for complicated molecules, the user may want to visualize the cavity surface. This can be accomplished by setting PrintLevel  , which will trigger the generation of several .PQR files that describe the cavity surface. (These are written to the Q-Chem output file.) The .PQR format is similar to the common .PDB (Protein Data Bank) format, but also contains charge and radius information for each atom. One of the output .PQR files contains the charges computed in the PCM calculation and radii (in Å) that are half of the square root of the surface area represented by each surface grid point. Thus, in examining this representation of the surface, larger discretization points are associated with larger surface areas. A second .PQR file contains the solute’s electrostatic potential (in atomic units), in place of the charge information, and uses uniform radii for the grid points. These .PQR files can be visualized using various third-party software, including the freely-available Visual Molecular Dynamics (VMD) program,[Humphrey et al.(1996)Humphrey, Dalke, and Schulten, VMD()] which is particularly useful for coloring the .PQR surface grid points according to their charge, and sizing them according to their contribution to the molecular surface area. (Examples of such visualizations can be found in Ref. Lange:2010a.)
, which will trigger the generation of several .PQR files that describe the cavity surface. (These are written to the Q-Chem output file.) The .PQR format is similar to the common .PDB (Protein Data Bank) format, but also contains charge and radius information for each atom. One of the output .PQR files contains the charges computed in the PCM calculation and radii (in Å) that are half of the square root of the surface area represented by each surface grid point. Thus, in examining this representation of the surface, larger discretization points are associated with larger surface areas. A second .PQR file contains the solute’s electrostatic potential (in atomic units), in place of the charge information, and uses uniform radii for the grid points. These .PQR files can be visualized using various third-party software, including the freely-available Visual Molecular Dynamics (VMD) program,[Humphrey et al.(1996)Humphrey, Dalke, and Schulten, VMD()] which is particularly useful for coloring the .PQR surface grid points according to their charge, and sizing them according to their contribution to the molecular surface area. (Examples of such visualizations can be found in Ref. Lange:2010a.)
PrintLevel
Controls the printing level during PCM calculations.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Prints PCM energy and basic surface grid information. Minimal additional printing.
1
Level 0 plus PCM solute-solvent interaction energy components and Gauss’ Law error.
2
Level 1 plus surface grid switching parameters and a .PQR file for visualization of
the cavity surface apparent surface charges.
3
Level 2 plus a .PQR file for visualization of the electrostatic potential at the surface
grid created by the converged solute.
4
Level 3 plus additional surface grid information, electrostatic potential and apparent
surface charges on each SCF cycle.
5
Level 4 plus extensive debugging information.
RECOMMENDATION:
Use the default unless further information is desired.
Finally, note that setting Method to Spherical in the $pcm input selection requests the construction of a solute cavity consisting of a single, fixed sphere. This is generally not recommended but is occasionally useful for making contact with the results of Born models in the literature, or the Kirkwood-Onsager model discussed in Section 12.2.1. In this case, the cavity radius and its center must also be specified in the $pcm section. The keyword HeavyPoints controls the number of Lebedev grid points used to discretize the surface.
CavityRadius
Specifies the solute cavity radius.
INPUT SECTION: $pcm
TYPE:
FLOAT
DEFAULT:
None
OPTIONS:
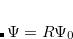
Use a radius of
, in Ångstroms.
RECOMMENDATION:
None.
CavityCenter
Specifies the center of the spherical solute cavity.
INPUT SECTION: $pcm
TYPE:
FLOAT
DEFAULT:
0.0 0.0 0.0
OPTIONS:


Coordinates of the cavity center, in Ångstroms.
RECOMMENDATION:
The format is CavityCenter followed by three floating-point values, delineated by spaces. Uses the same coordinate system as the $molecule section.
12.2.3.2 Examples
The following example shows a very basic PCM job. The solvent dielectric is specified in the $solvent section, which is described below.
Example 12.284 A basic example of using the PCMs: optimization of trifluoroethanol in water.
$rem
JOBTYPE OPT
BASIS 6-31G*
METHOD B3LYP
SOLVENT_METHOD PCM
$end
$pcm
Theory CPCM
Method SWIG
Solver Inversion
HeavyPoints 194
HPoints 194
Radii Bondi
vdwScale 1.2
$end
$solvent
Dielectric 78.39
$end
$molecule
0 1
C -0.245826 -0.351674 -0.019873
C 0.244003 0.376569 1.241371
O 0.862012 -0.527016 2.143243
F 0.776783 -0.909300 -0.666009
F -0.858739 0.511576 -0.827287
F -1.108290 -1.303001 0.339419
H -0.587975 0.878499 1.736246
H 0.963047 1.147195 0.961639
H 0.191283 -1.098089 2.489052
$end
The next example uses a single spherical cavity and should be compared to the Kirkwood-Onsager job, Example 12.12.1 on page *.
Example 12.285 PCM with a single spherical cavity, applied to H O in acetonitrile
O in acetonitrile
$molecule
0 1
O 0.00000000 0.00000000 0.11722303
H -0.75908339 0.00000000 -0.46889211
H 0.75908339 0.00000000 -0.46889211
$end
$rem
METHOD HF
BASIS 6-31g**
SOLVENT_METHOD pcm
$end
$pcm
method spherical ! single spherical cavity with 590 discretization points
HeavyPoints 590
CavityRadius 1.8 ! Solute Radius, in Angstrom
CavityCenter 0.0 0.0 0.0 ! Will be at center of Standard Nuclear Orientation
Theory SSVPE
$end
$solvent
Dielectric 35.9 ! Acetonitrile
$end
Finally, we consider an example of a united-atom cavity. Note that a user-defined van der Waals radius is supplied only for carbon, so the hydrogen radius is taken to be zero and thus the hydrogen atoms are not used to construct the cavity surface. (As mentioned above, the format for the $van_der_waals input section is discussion in Section 12.2.9).
Example 12.286 United-atom cavity construction for ethylene.
$comment
Benzene (in benzene), with a united-atom cavity construction
R = 2.28 A for carbon, R = 0 for hydrogen
$end
$molecule
0 1
C 1.38620 0.000000 0.000000
C 0.69310 1.200484 0.000000
C -0.69310 1.200484 0.000000
C -1.38620 0.000000 0.000000
C -0.69310 -1.200484 0.000000
C 0.69310 -1.200484 0.000000
H 2.46180 0.000000 0.000000
H 1.23090 2.131981 0.000000
H -1.23090 2.131981 0.000000
H -2.46180 0.000000 0.000000
H -1.23090 -2.131981 0.000000
H 1.23090 -2.131981 0.000000
$end
$rem
EXCHANGE hf
BASIS 6-31G*
SOLVENT_METHOD pcm
$end
$pcm
theory iefpcm ! this is a synonym for ssvpe
method swig
printlevel 1
radii read
$end
$solvent
dielectric 2.27
$end
$van_der_waals
1
6 2.28
1 0.00
$end
12.2.3.3 $solvent section
The solvent for PCM calculations is specified using the $solvent section, as documented below. In addition, the $solvent section can be used to incorporate non-electrostatic interaction terms into the solvation energy. (The Theory keyword in the $pcm section specifies only how the electrostatic interactions are handled.) The general form of the $solvent input section is shown below. The $solvent section was used above to specify parameters for the Kirkwood-Onsager SCRF model, and will be used again below to specify the solvent for SM calculations (Section 12.2.8); in each case, the particular options that can be listed in the $solvent section depend upon the value of the $rem variable SOLVENT_METHOD.
calculations (Section 12.2.8); in each case, the particular options that can be listed in the $solvent section depend upon the value of the $rem variable SOLVENT_METHOD.
$solvent
NonEls <Option>
NSolventAtoms <Number unique of solvent atoms>
SolventAtom <Number1> <Number2> <Number3> <SASradius>
SolventAtom <Number1> <Number2> <Number3> <SASradius>
. . .
<Keyword> <parameter/option>
. . .
$end
The keyword SolventAtom requires multiple parameters, whereas all other keywords require only a single parameter. In addition to any (optional) non-electrostatic parameters, the $solvent section is also used to specify the solvent’s dielectric constant. If non-electrostatic interactions are ignored, then this is the only keyword that is necessary in the $solvent section. For nonequilibrium TDDFT/C-PCM calculations (Section 12.2.2.3), the optical dielectric constant should be specified in the $solvent section as well.
Dielectric
The (static) dielectric constant of the PCM solvent.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
78.39
OPTIONS:

Use a dielectric constant of
.
RECOMMENDATION:
The static (i.e., zero-frequency) dielectric constant is what is usually called “the” dielectric constant. The default corresponds to water at 25
C.
OpticalDielectric
The optical dielectric constant of the PCM solvent.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
1.78
OPTIONS:

Use an optical dielectric constant of
.
RECOMMENDATION:
The default corresponds to water at 25
C. Note that
, where
is the solvent’s index of refraction.
The non-electrostatic interactions currently available in Q-Chem are based on the work of Cossi et al.,[Cossi et al.(1996)Cossi, Mennucci, and Cammi] and are computed outside of the SCF procedure used to determine the electrostatic interactions. The non-electrostatic energy is highly dependent on the input parameters and can be extremely sensitive to the radii chosen to define the solute cavity. Accordingly, the inclusion of non-electrostatic interactions is highly empirical and probably needs to be considered on a case-by-case basis. Following Ref. Cossi:1996, the cavitation energy is computed using the same solute cavity that is used to compute the electrostatic energy, whereas the dispersion/repulsion energy is computed using a solvent-accessible surface.
The following keywords (in the $solvent section) are used to define non-electrostatic parameters for PCM calculations.
NonEls
Specifies what type of non-electrostatic contributions to include.
INPUT SECTION: $solvent
TYPE:
STRING
DEFAULT:
None
OPTIONS:
Cav
Cavitation energy
Buck
Buckingham dispersion and repulsion energy from atomic number
LJ
Lennard-Jones dispersion and repulsion energy from force field
BuckCav
Buck + Cav
LJCav
LJ + Cav
RECOMMENDATION:
A very limited set of parameters for the Buckingham potential is available at present.
NSolventAtoms
The number of different types of atoms.
INPUT SECTION: $solvent
TYPE:
INTEGER
DEFAULT:
None
OPTIONS:

Specifies that there are
different types of atoms.
RECOMMENDATION:
This keyword is necessary when NonEls = Buck, LJ, BuckCav, or LJCav. Methanol (
), for example, has three types of atoms (C, H, and O).
SolventAtom
Specifies a unique solvent atom.
INPUT SECTION: $solvent
TYPE:
Various
DEFAULT:
None.
OPTIONS:
Input (TYPE)
Description
Number1 (INTEGER):
The atomic number of the atom
Number2 (INTEGER):
How many of this atom are in a solvent molecule
Number3 (INTEGER):
Force field atom type
SASradius (FLOAT):
Probe radius (in Å) for defining the solvent accessible surface
RECOMMENDATION:
If not using LJ or LJCav, Number3 should be set to 0. The SolventAtom keyword is necessary when NonEls = Buck, LJ, BuckCav, or LJCav.
Temperature
Specifies the solvent temperature.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
300.0
OPTIONS:
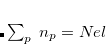
Use a temperature of
, in Kelvin.
RECOMMENDATION:
Used only for the cavitation energy.
Pressure
Specifies the solvent pressure.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
1.0
OPTIONS:

Use a pressure of
, in bar.
RECOMMENDATION:
Used only for the cavitation energy.
SolventRho
Specifies the solvent number density
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
Determined for water, based on temperature.
OPTIONS:
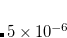
Use a density of
, in molecules/Å
.
RECOMMENDATION:
Used only for the cavitation energy.
SolventRadius
The radius of a solvent molecule of the PCM solvent.
INPUT SECTION: $solvent
TYPE:
FLOAT
DEFAULT:
None
OPTIONS:
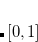
Use a radius of
, in Å.
RECOMMENDATION:
Used only for the cavitation energy.
The following example illustrates the use of the non-electrostatic interactions.
Example 12.287 Optimization of trifluoroethanol in water using both electrostatic and non-electrostatic PCM interactions. OPLSAA parameters are used in the Lennard-Jones potential for dispersion and repulsion.
$rem
JOBTYPE OPT
BASIS 6-31G*
METHOD B3LYP
SOLVENT_METHOD PCM
FORCE_FIELD OPLSAA
$end
$pcm
Theory CPCM
Method SWIG
Solver Inversion
HeavyPoints 194
HPoints 194
Radii Bondi
vdwScale 1.2
$end
$solvent
NonEls LJCav
NSolventAtoms 2
SolventAtom 8 1 186 1.30
SolventAtom 1 2 187 0.01
SolventRadius 1.35
Temperature 298.15
Pressure 1.0
SolventRho 0.03333
Dielectric 78.39
$end
$molecule
0 1
C -0.245826 -0.351674 -0.019873 23
C 0.244003 0.376569 1.241371 22
O 0.862012 -0.527016 2.143243 24
F 0.776783 -0.909300 -0.666009 26
F -0.858739 0.511576 -0.827287 26
F -1.108290 -1.303001 0.339419 26
H -0.587975 0.878499 1.736246 27
H 0.963047 1.147195 0.961639 27
H 0.191283 -1.098089 2.489052 25
$end
12.2.3.4 Job control and Examples for Non-Equilibrium Solvation
The OpticalDielectric keyword in $solvent is always needed. The LR energy is automatically calculated while the CIS/TDDFT calculations are performed with PCM, but it is turned off while the perturbation scheme is employed.
ChargeSeparation
Partition fast and slow charges in solvent equilibrium state
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
No default.
OPTIONS:
Marcus
Do slow-fast charge separation in the ground state.
Excited
Do slow-fast charge separation in an excited-state.
RECOMMENDATION:
Charge separation is used in conjunction with the StateSpecific keyword in $pcm.
StateSpecific
Specifies which the state-specific method will be used.
INPUT SECTION: $pcm
TYPE:
Various
DEFAULT:
No default.
OPTIONS:
Marcus
Run self-consistent SS method in the ground-state with a given slow polarization charges.
Perturb
Perform ptSS and ptLR for vertical excitations.

The
th excited-state used for charge separation (for emission).
RECOMMENDATION:
NoneqGrad
Control whether perform excited state geometry optimization in equilibrium or nonequilibrium.
INPUT SECTION: $pcm
TYPE:
NONE
DEFAULT:
No default.
OPTIONS:
RECOMMENDATION:
Specify it for nonequilibrium optimization otherwise equilibrium geometry optimization will be performed.
Example 12.288 LR-TDDFT/C-PCM low-lying vertical excitation energy
$molecule
0 1
C 0 0 0.0
O 0 0 1.21
$end
$rem
EXCHANGE B3LYP
CIS_N_ROOTS 10
CIS_SINGLETS TRUE
CIS_TRIPLETS TRUE
RPA TRUE
BASIS 6-31+G*
SOLVENT_METHOD PCM
$end
$pcm
Theory CPCM
Method SWIG
Solver Inversion
Radii Bondi
$end
$solvent
Dielectric 78.39
OpticalDielectric 1.777849
$end
Example 12.289 PCM solvation effects on the vertical excitation energies of planar DMABN using the ptSS and ptLR methods.
$molecule
0 1
C 0.000046 -0.000398 1.904953
C 1.210027 0.000379 1.186051
C 1.214640 -0.000065 -0.194515
C 0.000164 -0.000616 -0.933832
C -1.214349 -0.001557 -0.194687
C -1.209753 -0.001846 1.185775
H 2.151949 0.001377 1.722018
H 2.164371 0.000481 -0.709640
H -2.164082 -0.002008 -0.709781
H -2.151763 -0.002287 1.721615
C -0.000227 0.001061 3.325302
N -0.000475 0.002405 4.484321
N 0.000053 -0.000156 -2.297372
C -1.258656 0.001284 -3.036994
H -1.041042 0.001615 -4.102376
H -1.860897 -0.885647 -2.811117
H -1.859247 0.889133 -2.810237
C 1.258563 -0.000660 -3.037285
H 1.860651 0.886208 -2.810755
H 1.859362 -0.888604 -2.811461
H 1.040664 -0.000097 -4.102609
$end
$rem
EXCHANGE LRC-wPBEPBE
OMEGA 260
BASIS 6-31G*
CIS_N_ROOTS 10
RPA 2
CIS_SINGLETS 1
CIS_TRIPLETS 0
CIS_DYNAMIC_MEM TRUE
CIS_RELAXED_DENSITY TRUE
USE_NEW_FUNCTIONAL TRUE
SOLVENT_METHOD PCM
PCM_PRINT 1
$end
$pcm
NonEquilibrium
Theory IEFPCM
StateSpecific Perturb
$end
$solvent
Dielectric 35.688000 ! Acetonitrile
OpticalDielectric 1.806874
$end
Example 12.290 Aqueous phenol ionization using state-specific nonequilibrium PCM
$molecule
0 1
C -0.189057 -1.215927 -0.000922
H -0.709319 -2.157526 -0.001587
C 1.194584 -1.155381 -0.000067
H 1.762373 -2.070036 -0.000230
C 1.848872 0.069673 0.000936
H 2.923593 0.111621 0.001593
C 1.103041 1.238842 0.001235
H 1.595604 2.196052 0.002078
C -0.283047 1.185547 0.000344
H -0.862269 2.095160 0.000376
C -0.929565 -0.042566 -0.000765
O -2.287040 -0.159171 -0.001759
H -2.663814 0.725029 0.001075
$end
$rem
EXCHANGE wPBE
CORRELATION PBE
LRC_DFT 1
OMEGA 300
BASIS 6-31+G*
SCF_CONVERGENCE 8
SOLVENT_METHOD PCM
PCM_PRINT 1
$end
$pcm
NonEquilibrium
$end
$solvent
Dielectric 78.39
OpticalDielectric 1.777849
$end
@@@
$molecule
1 2
read
$end
$rem
EXCHANGE wPBE
CORRELATION PBE
LRC_DFT 1
OMEGA 300
BASIS 6-31+G*
SCF_CONVERGENCE 8
SOLVENT_METHOD PCM
PCM_PRINT 1
SCF_GUESS READ
$end
$pcm
StateSpecific Marcus
$end
$solvent
Dielectric 78.39
OpticalDielectric 1.777849
$end
Example 12.291 PCM solvation effects on the emission energy of twisted DMABN in acetonitrile.
$molecule
0 1
C -0.000002 -0.000003 1.894447
C 1.230178 0.000003 1.160765
C 1.244862 0.000001 -0.200360
C 0.000003 -0.000013 -0.917901
C -1.244845 -0.000000 -0.200354
C -1.230160 0.000000 1.160753
H 2.171128 0.000013 1.704064
H 2.180670 0.000009 -0.750140
H -2.180657 0.000006 -0.750120
H -2.171112 0.000006 1.704037
C -0.000023 -0.000002 3.293509
N -0.000011 -0.000001 4.459415
N -0.000008 -0.000005 -2.309193
C 0.000001 1.253881 -3.021235
H 0.000005 1.099076 -4.098660
H -0.882908 1.818975 -2.705815
H 0.882911 1.818967 -2.705805
C -0.000009 -1.253886 -3.021246
H 0.882917 -1.818966 -2.705849
H -0.882901 -1.818992 -2.705803
H -0.000038 -1.099071 -4.098670
$end
$rem
EXCHANGE LRC-wPBEPBE
OMEGA 280
BASIS 6-31G*
CIS_N_ROOTS 10
RPA 2
CIS_SINGLETS 1
CIS_TRIPLETS 0
CIS_DYNAMIC_MEM TRUE
CIS_RELAXED_DENSITY TRUE
USE_NEW_FUNCTIONAL TRUE
SOLVENT_METHOD PCM
PCM_PRINT 1
$end
$pcm
ChargeSeparation Excited
StateSpecific 1
$end
$solvent
Dielectric 35.688000 ! Acetonitrile
OpticalDielectric 1.806874
$end
@@@
$molecule
READ
$end
$rem
EXCHANGE LRC-wPBEPBE
OMEGA 280
BASIS 6-31G*
SCF_GUESS READ
SCF_CONVERGENCE 8
SOLVENT_METHOD PCM
PCM_PRINT 1
$end
$pcm
StateSpecific Marcus
$end
$solvent
Dielectric 35.688000 ! Acetonitrile
OpticalDielectric 1.806874
$end
12.2.4 Linear-Scaling QM/MM/PCM Calculations
Recall that PCM electrostatics calculations require the solution of the set of linear equations given in Eq. eq:Kq=Rv, to determine the vector  of apparent surface charges. The precise forms of the matrices
of apparent surface charges. The precise forms of the matrices  and
and  depend upon the particular PCM (Table 12.3), but in any case they have dimension
depend upon the particular PCM (Table 12.3), but in any case they have dimension  , where
, where  is the number of Lebedev grid points used to discretize the cavity surface. Construction of the matrix
is the number of Lebedev grid points used to discretize the cavity surface. Construction of the matrix  affords a numerically exact solution to Eq. eq:Kq=Rv, whose cost scales as
affords a numerically exact solution to Eq. eq:Kq=Rv, whose cost scales as  in CPU time and
in CPU time and  in memory. This cost is exacerbated by smooth PCMs, which discard fewer interior grid points so that
in memory. This cost is exacerbated by smooth PCMs, which discard fewer interior grid points so that  tends to be larger, for a given solute, as compared to traditional discretization schemes. For QM solutes, the cost of inverting
tends to be larger, for a given solute, as compared to traditional discretization schemes. For QM solutes, the cost of inverting  is usually negligible relative to the cost of the electronic structure calculation, but for the large values of
is usually negligible relative to the cost of the electronic structure calculation, but for the large values of  that are encountered in MM/PCM or QM/MM/PCM jobs, the
that are encountered in MM/PCM or QM/MM/PCM jobs, the  cost of inverting
cost of inverting  is often prohibitively expensive.
is often prohibitively expensive.
To avoid this bottleneck, Lange and Herbert[Herbert and Lange(2016)] have developed an iterative conjugate gradient (CG) solver for Eq. eq:Kq=Rv whose cost scales as  in CPU time and
in CPU time and  in memory. A number of other cost-saving options are available, including efficient pre-conditioners and matrix factorizations that speed up convergence of the CG iterations, and a fast multipole algorithm for computing the electrostatic interactions.[Li et al.(2009)Li, Johnston, and Krasny] Together, these features lend themselves to a solution of Eq. eq:Kq=Rv whose cost scales as
in memory. A number of other cost-saving options are available, including efficient pre-conditioners and matrix factorizations that speed up convergence of the CG iterations, and a fast multipole algorithm for computing the electrostatic interactions.[Li et al.(2009)Li, Johnston, and Krasny] Together, these features lend themselves to a solution of Eq. eq:Kq=Rv whose cost scales as  in both memory and CPU time, for sufficiently large systems.[Herbert and Lange(2016)] Currently, these options are available only for C-PCM, not for SS(V)PE/IEF-PCM.
in both memory and CPU time, for sufficiently large systems.[Herbert and Lange(2016)] Currently, these options are available only for C-PCM, not for SS(V)PE/IEF-PCM.
Listed below are job control variables for the CG solver, which should be specified within the $pcm input section. Researchers who use this feature are asked to cite the original SWIG PCM references[Lange and Herbert(2010b), Lange and Herbert(2011)] as well as the reference for the CG solver.[Herbert and Lange(2016)]
Solver
Specifies the algorithm used to solve the PCM equations.
INPUT SECTION: $pcm
TYPE:
STRING
DEFAULT:
INVERSION
OPTIONS:
INVERSION
Direct matrix inversion
CG
Iterative conjugate gradient
RECOMMENDATION:
Matrix inversion is faster for small solutes because it needs to be performed only once in a single-point calculation. However, the CG solver (which must be applied at each SCF iteration) is recommended for large MM/PCM or QM/MM/PCM calculations.
CGThresh
The threshold for convergence of the conjugate gradient solver.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
6
OPTIONS:

Conjugate gradient converges when the maximum residual is less than
.
RECOMMENDATION:
The default typically affords PCM energies on par with the precision of matrix inversion for small systems. For systems that have difficulty with SCF convergence, one should increase
or try the matrix inversion solver. For well-behaved or very large systems, a smaller
might be permissible.
DComp
Controls decomposition of matrices to reduce the matrix norm for the CG Solver.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
0
Turns off matrix decomposition
1
Turns on matrix decomposition
3
Option 1 plus only stores upper half of matrix and enhances gradient evaluation
RECOMMENDATION:
None
PreCond
Controls the use of the pre-conditioner for the CG solver.
INPUT SECTION: $pcm
TYPE:
None
DEFAULT:
Off
OPTIONS:
No options. Specify the keyword to enable pre-conditioning.
RECOMMENDATION:
A Jacobi block-diagonal pre-conditioner is applied during the conjugate gradient algorithm to improve the rate of convergence. This reduces the number of CG iterations, at the expense of some overhead. Pre-conditioning is generally recommended for large systems.
NoMatrix
Specifies whether PCM matrices should be explicitly constructed and stored.
INPUT SECTION: $pcm
TYPE:
None
DEFAULT:
Off
OPTIONS:
No options. Specify the keyword to avoid explicit construction of PCM matrices.
RECOMMENDATION:
Storing the PCM matrices requires
memory. If this is prohibitive, the NoMatrix option forgoes explicit construction of the PCM matrices, and instead constructs the matrix elements as needed, reducing the memory requirement to
at the expense of additional computation.
UseMultipole
Controls the use of the adaptive fast multipole method in the CG solver.
INPUT SECTION: $pcm
TYPE:
None
DEFAULT:
Off
OPTIONS:
No options. Specify the keyword in order to enable the fast multipole method.
RECOMMENDATION:
The fast multipole approach formally reduces the CPU time to
, but is only beneficial for spatially extended systems with several thousand cavity grid points. Requires the use of NoMatrix.
MultipoleOrder
Specifies the highest multipole order to use in the FMM.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
4
OPTIONS:

The highest order multipole in the multipole expansion.
RECOMMENDATION:
Increasing the multipole order improves accuracy but also adds more computational expense. The default yields satisfactory performance in common QM/MM/PCM applications.
Theta
The multipole acceptance criterion.
INPUT SECTION: $pcm
TYPE:
FLOAT
DEFAULT:
0.6
OPTIONS:

A number between zero and one.
RECOMMENDATION:
The default is recommended for general usage. This variable determines when the use of a multipole expansion is valid. For a given grid point and box center in the FMM, a multipole expansion is accepted when
Theta, where
is the distance from the grid point to the box center and
is the radius of the box. Setting Theta to one will accept all multipole expansions, whereas setting it to zero will accept none. If not accepted, the grid point’s interaction with each point inside the box is computed explicitly. A low Theta is more accurate but also more expensive than a higher Theta.
NBox
The FMM boxing threshold.
INPUT SECTION: $pcm
TYPE:
INTEGER
DEFAULT:
100
OPTIONS:

The maximum number of grid points for a leaf box.
RECOMMENDATION:
The default is recommended. This option is for advanced users only. The adaptive FMM boxing algorithm divides space into smaller and smaller boxes until each box has less than or equal to NBox grid points. Modification of the threshold can lead to speedup or slowdown depending on the molecular system and other FMM variables.
A sample input file for the linear-scaling QM/MM/PCM methodology can be found in the $QC/samples directory, under the name QMMMPCM_crambin.in. This sample involves a QM/MM description of a protein (crambin) in which a single tyrosine side chain is taken to be the QM region. The entire protein is immersed in a dielectric using C-PCM with SWIG discretization.
12.2.5 Isodensity Implementation of SS(V)PE
12.2.5.1 Basic Job Control
As discussed above, results obtained various types of PCMs are quite sensitive to the details of the cavity construction. Q-Chem’s implementation of PCMs, using Lebedev grids, simplifies this construction somewhat, but leaves the radii of the atomic spheres as empirical parameters (albeit ones for which widely-used default values are provided). An alternative implementation of the SS(V)PE solvation model is also available,[Chipman and Dupuis(2002)] which attempts to further eliminate empiricism associated with cavity construction by taking the cavity surface to be a specified iso-contour of the solute’s electron density. [We call this the isodensity implementation of SS(V)PE in Table 12.3, and it is based on Chipman’s “symmetrized” form of the  matrix.[Chipman and Dupuis(2002), Lange and Herbert(2011)]] In this case, the cavity surface is discretized by projecting a single-center Lebedev grid onto the iso-contour surface. Unlike the PCM implementation discussed in Section 12.2.2, for which point-group symmetry is disabled, this implementation of SS(V)PE supports full symmetry for all Abelian point groups. The larger and/or the less spherical the solute molecule is, the more points are needed to get satisfactory precision in the results. Further experience will be required to develop detailed recommendations for this parameter. Values as small as 110 points are usually sufficient for diatomic or triatomic molecules. The default value of 1202 points is adequate to converge the energy within 0.1 kcal/mol for solutes the size of mono-substituted benzenes.
matrix.[Chipman and Dupuis(2002), Lange and Herbert(2011)]] In this case, the cavity surface is discretized by projecting a single-center Lebedev grid onto the iso-contour surface. Unlike the PCM implementation discussed in Section 12.2.2, for which point-group symmetry is disabled, this implementation of SS(V)PE supports full symmetry for all Abelian point groups. The larger and/or the less spherical the solute molecule is, the more points are needed to get satisfactory precision in the results. Further experience will be required to develop detailed recommendations for this parameter. Values as small as 110 points are usually sufficient for diatomic or triatomic molecules. The default value of 1202 points is adequate to converge the energy within 0.1 kcal/mol for solutes the size of mono-substituted benzenes.
Energy gradients are also not available for this implementation of SS(V)PE, although they are available for the implementation described in Section 12.2.2 in which the cavity is constructed from atom-centered spheres. As with the PCMs discussed in that section, the solute may be described using Hartree-Fock theory or DFT; post-Hartree–Fock correlated wave functions can also take advantage of molecular orbitals that are polarized using SS(V)PE. Researchers who use the isodensity SS(V)PE feature are asked to cite Ref. Chipman:2000.
In related work, Pomogaeva and Chipman[Pomogaeva and Chipman(2011), Pomogaeva and Chipman(2013), Pomogaeva and Chipman(2014), Pomogaeva and Chipman(2015)] recently introduced a “composite method for implicit representation of solvent” (CMIRS) that is based on SS(V)PE electrostatics but adds non-electrostatic terms. This model is available in Q-Chem[You and Herbert(2016)] and is discussed in Section 12.2.6. In its current implementation, CMIRS requires an isodensity SS(V)PE calculation, However, the current implementation computes the non-electrostatic interactions using the cavity and the solute’s charge density generated from the isodensity SS(V)PE. To use the CMIRS model, an isodensity SS(V)PE calculation must be requested (as described below), and the IDEFESR must be set to 1 in the $svp input section (see Section 12.2.5.2).
An isodensity SS(V)PE calculation is requested by setting SOLVENT_METHOD = ISOSVP in the $rem section, in addition to normal job control variables for a single-point energy calculation. Whereas the other solvation models described in this chapter use specialized input sections (e.g., $pcm) in lieu of a slew of $rem variables, the isodensity SS(V)PE code is an interface between Q-Chem and a code written by Chipman,[Chipman and Dupuis(2002)] so some $rem variables are used for job control of isodensity SS(V)PE calculations. These are listed below.
SVP_MEMORY
Specifies the amount of memory for use by the solvation module.
TYPE:
INTEGER
DEFAULT:
125
OPTIONS:
corresponds to the amount of memory in Mb.
RECOMMENDATION:
The default should be fine for medium size molecules with the default Lebedev grid, only increase if needed.
SVP_PATH
Specifies whether to run a gas phase computation prior to performing the solvation procedure.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
runs a gas-phase calculation and after
convergence runs the SS(V)PE computation.
1
does not run a gas-phase calculation.
RECOMMENDATION:
Running the gas-phase calculation provides a good guess to start the solvation stage and provides a more complete set of solvated properties.
SVP_CHARGE_CONV
Determines the convergence value for the charges on the cavity. When the change in charges fall below this value, if the electron density is converged, then the calculation is considered converged.
TYPE:
INTEGER
DEFAULT:
7
OPTIONS:

Convergence threshold set to
.
RECOMMENDATION:
The default value unless convergence problems arise.
SVP_CAVITY_CONV
Determines the convergence value of the iterative isodensity cavity procedure.
TYPE:
INTEGER
DEFAULT:
10
OPTIONS:

Convergence threshold set to
.
RECOMMENDATION:
The default value unless convergence problems arise.
SVP_GUESS
Specifies how and if the solvation module will use a given guess for the charges and cavity points.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
No guessing.
1
Read a guess from a previous Q-Chem solvation computation.
2
Use a guess specified by the $svpirf section from the input
RECOMMENDATION:
It is helpful to also set SCF_GUESS to READ when using a guess from a previous Q-Chem run.
This last $rem variable requires specification of a $svpirf input section, the format for which is the following:
$svpirf
<# point> <x point> <y point> <z point> <charge> <grid weight>
<# point> <x normal> <y normal> <z normal>
$end
12.2.5.2 The $svp Input Section
More refined control over SS(V)PE jobs is obtained using a $svp input section. These are read directly by Chipman’s SS(V)PE solvation module and therefore must be specified in the context of a FORTRAN namelist. The format is as follows:
$svp
<KEYWORD>=<VALUE>, <KEYWORD>=<VALUE>,...
<KEYWORD>=<VALUE>
$end
For example, the section may look like this:
$svp
RHOISO=0.001, DIELST=78.39, NPTLEB=110
$end
The following keywords are supported in the $svp section:
DIELST
The static dielectric constant.
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
78.39
OPTIONS:
real number specifying the constant.
RECOMMENDATION:
The default value 78.39 is appropriate for water solvent.
IDEFESR
Specifies whether to request a CMIRS calculation.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
do not invoke a CMIRS calculation.
1
do invoke a CMIRS calculation.
RECOMMENDATION:
ISHAPE
A flag to set the shape of the cavity surface.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
use the electronic isodensity surface.
1
use a spherical cavity surface.
RECOMMENDATION:
Use the default surface.
RHOISO
Value of the electronic isodensity contour used to specify the cavity surface. (Only relevant for ISHAPE = 0.)
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
0.001
OPTIONS:
Real number specifying the density in electrons/bohr
.
RECOMMENDATION:
The default value is optimal for most situations. Increasing the value produces a smaller cavity which ordinarily increases the magnitude of the solvation energy.
RADSPH
Sphere radius used to specify the cavity surface (Only relevant for ISHAPE=1.)
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
Half the distance between the outermost atoms plus 1.4 Ångstroms.
OPTIONS:
Real number specifying the radius in bohr (if positive) or in Ångstroms (if negative).
RECOMMENDATION:
Make sure that the cavity radius is larger than the length of the molecule.
INTCAV
A flag to select the surface integration method.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Single center Lebedev integration.
1
Single center spherical polar integration.
RECOMMENDATION:
The Lebedev integration is by far the more efficient.
NPTLEB
The number of points used in the Lebedev grid for the single-center surface integration. (Only relevant if INTCAV = 0.)
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
1202
OPTIONS:
Valid choices are:
6, 18, 26, 38, 50, 86, 110, 146, 170, 194, 302, 350, 434, 590, 770,
974, 1202, 1454, 1730, 2030, 2354, 2702, 3074, 3470, 3890, 4334,
4802, or 5294.
RECOMMENDATION:
The default value has been found adequate to obtain the energy to within 0.1 kcal/mol for solutes the size of mono-substituted benzenes.
NPTTHE, NPTPHI
The number of (
,
) points used for single-centered surface integration (relevant only if INTCAV = 1.)
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
8,16
OPTIONS:
,
specifying the number of points.
RECOMMENDATION:
These should be multiples of 2 and 4 respectively, to provide symmetry sufficient for all Abelian point groups. Defaults are too small for all but the tiniest and simplest solutes.
LINEQ
Flag to select the method for solving the linear equations that determine the apparent point charges on the cavity surface.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
0
use LU decomposition in memory if space permits, else switch to LINEQ = 2
1
use conjugate gradient iterations in memory if space permits, else use LINEQ = 2
2
use conjugate gradient iterations with the system matrix stored externally on disk.
RECOMMENDATION:
The default should be sufficient in most cases.
CVGLIN
Convergence criterion for solving linear equations by the conjugate gradient iterative method (relevant if LINEQ = 1 or 2.)
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
1.0E-7
OPTIONS:
Real number specifying the actual criterion.
RECOMMENDATION:
The default value should be used unless convergence problems arise.
Note that the single-center surface integration approach that is used to find the isodensity surface may fail for certain very non-spherical solute molecules. The program will automatically check for this, aborting with a warning message if necessary. The single-center approach succeeds only for what is called a “star surface”, meaning that an observer sitting at the center has an unobstructed view of the entire surface. Said another way, for a star surface any ray emanating out from the center will pass through the surface only once. Some cases of failure may be fixed by simply moving to a new center with the ITRNGR parameter described below. But some surfaces are inherently non-star surfaces and cannot be treated with this program until more sophisticated surface integration approaches are developed and implemented.
ITRNGR
Translation of the cavity surface integration grid.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
2
OPTIONS:
0
No translation (i.e., center of the cavity at the origin
of the atomic coordinate system)
1
Translate to the center of nuclear mass.
2
Translate to the center of nuclear charge.
3
Translate to the midpoint of the outermost atoms.
4
Translate to midpoint of the outermost non-hydrogen atoms.
5
Translate to user-specified coordinates in Bohr.
6
Translate to user-specified coordinates in Ångstroms.
RECOMMENDATION:
The default value is recommended unless the single-center integrations procedure fails.
TRANX, TRANY, TRANZ
,
, and
value of user-specified translation (only relevant if ITRNGR is set to 5 or 6).
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
0, 0, 0
OPTIONS:
,
, and
relative to the origin in the appropriate units.
RECOMMENDATION:
None.
IROTGR
Rotation of the cavity surface integration grid.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
2
OPTIONS:
0
No rotation.
1
Rotate initial
axes of the integration grid to coincide
with principal moments of nuclear inertia (relevant if ITRNGR = 1)
2
Rotate initial
axes of integration grid to coincide with
principal moments of nuclear charge (relevant if ITRNGR = 2)
3
Rotate initial
axes of the integration grid through user-specified
Euler angles as defined by Wilson, Decius, and Cross.
RECOMMENDATION:
The default is recommended unless the knowledgeable user has good reason otherwise.
ROTTHE ROTPHI ROTCHI
Euler angles (
,
,
) in degrees for user-specified rotation of the cavity surface (relevant if IROTGR = 3).
INPUT SECTION: $svp
TYPE:
FLOAT
DEFAULT:
0,0,0
OPTIONS:
,
,
in degrees
RECOMMENDATION:
None.
IOPPRD
Specifies the choice of system operator form.
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Symmetric form.
1
Non-symmetric form.
RECOMMENDATION:
The default uses more memory but is generally more efficient, we recommend its use unless there is shortage of memory available.
By default, Q-Chem will check the validity of the single-center expansion by searching for the isodensity surface in two different ways: first, working inwards from a large distance, and next by working outwards from the origin. If the same result is obtained (within tolerances) using both procedures, then the cavity is accepted. If the two results do not agree, then the program exits with an error message indicating that the inner isodensity surface is found to be too far from the outer isodensity surface.
Some molecules, for example C , can have a hole in the middle. Such molecules have two different “legal” isodensity surfaces, a small inner one inside the “hole”, and a large outer one that is the desired surface for solvation. In such cases, the cavity check described in the preceding paragraph causes the program to exit. To avoid this, one can consider turning off the cavity check that works out from the origin, leaving only the outer cavity determined by working in from large distances.
, can have a hole in the middle. Such molecules have two different “legal” isodensity surfaces, a small inner one inside the “hole”, and a large outer one that is the desired surface for solvation. In such cases, the cavity check described in the preceding paragraph causes the program to exit. To avoid this, one can consider turning off the cavity check that works out from the origin, leaving only the outer cavity determined by working in from large distances.
ICVICK
Specifies whether to perform cavity check
INPUT SECTION: $svp
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
0
no cavity check, use only the outer cavity
1
cavity check, generating both the inner and outer cavities and compare.
RECOMMENDATION:
Consider turning off cavity check only if the molecule has a hole and if a star (outer) surface is expected.
12.2.6 Composite Method for Implicit Representation of Solvent (CMIRS)
Whereas PCMs, including sophisticated ones like SS(V)PE and IEF-PCM, account for long-range solute–solvent interactions, an accurate model for free energies of solvation must also include a treatment of short-range, non-electrostatic interactions. Various models decompose these interactions in different ways, but usually the non-electrostatic terms attempt to model all or most of the following: solute–solvent dispersion (van der Waals) interactions, Pauli (exchange) repulsion between solute and solvent, the work associated with forming the solute cavity within the dielectric medium (the so-called “cavitation energy”), hydrogen-bonding and other specific interactions due to the molecular structure of the solvent, and changes in the structure (and therefore the entropy) of the neat solvent upon introduction of the solute
Pomogaeva and Chipman[Pomogaeva and Chipman(2011), Pomogaeva and Chipman(2013), Pomogaeva and Chipman(2014), Pomogaeva and Chipman(2015)] have introduced an implicit solvation model that attempts to model these non-electrostatic interactions alongside a PCM-style treatment of the bulk electrostatics. They call this approach the “composite method for implicit representation of solvent” (CMIRS), and it consists first of a self-consistent treatment of solute–continuum electrostatics using the SS(V)PE model (Section 12.2.5). To this electrostatics calculation, CMIRS adds a solute–solvent dispersion term that is modeled upon the non-local VV09 van der Waals dispersion density functional,[Vydrov and Van Voorhis(2009)] a Pauli repulsion contribution that depends upon the tail of the solute’s electron density that extends beyond the solute cavity, and a hydrogen-bonding correction based on the maximum and minimum values of the normal component of the electric field generated by the solute at the cavity surface. The Gibbs free energy of solvation is thus modeled as
 |
(12.13) |
where  is the continuum electrostatics contribution from the SS(V)PE model, which is based on a solute cavity defined as an isocontour
is the continuum electrostatics contribution from the SS(V)PE model, which is based on a solute cavity defined as an isocontour  of the solute’s charge density. The second term contains the short-range dispersion, exchange, and "field-extremum short-range" (DEFESR) interactions:
of the solute’s charge density. The second term contains the short-range dispersion, exchange, and "field-extremum short-range" (DEFESR) interactions:
 |
(12.15) |
These terms are evaluated only once, using a converged charge density for the solute from a SS(V)PE calculation.
The CMIRS approach was implemented in Q-Chem by Zhi-Qiang You and John Herbert.[You and Herbert(2016)] In the course of this work, a serious error was discovered in the the original implementation of  by Pomogaeva and Chipman, in the gamess program. Although reparameterization of a corrected version of the model leads to only small changes in the overall error statistics across a large database of experimental free energies of solvation, the apportionment between energy components in Eq. eq:DEFESR-free-energy changes significantly.[You and Herbert(2016)] By request of Dan Chipman, the Q-Chem implementation is termed “CMIRS v. 1.1", reserving v. 1.0 for the original gamess implementation of Pomogaeva and Chipman.
by Pomogaeva and Chipman, in the gamess program. Although reparameterization of a corrected version of the model leads to only small changes in the overall error statistics across a large database of experimental free energies of solvation, the apportionment between energy components in Eq. eq:DEFESR-free-energy changes significantly.[You and Herbert(2016)] By request of Dan Chipman, the Q-Chem implementation is termed “CMIRS v. 1.1", reserving v. 1.0 for the original gamess implementation of Pomogaeva and Chipman.
The CMIRS model is independently parametrized for each solvent of interest, but uses no more than five empirical parameters per solvent. It is presently available in Q-Chem for water, acetonitrile, dimethyl sulfoxide, benzene, and cyclohexane. Error statistics for  compare very favorably to those of the SM
compare very favorably to those of the SM models that are described in Section 12.2.8, e.g., mean unsigned errors
models that are described in Section 12.2.8, e.g., mean unsigned errors  kcal/mol in benzene and cyclohexane and
kcal/mol in benzene and cyclohexane and  kcal/mol in water. The latter statistic includes challenging ionic solutes; errors for charge-neutral aqueous solutes are smaller still.[You and Herbert(2016)]
kcal/mol in water. The latter statistic includes challenging ionic solutes; errors for charge-neutral aqueous solutes are smaller still.[You and Herbert(2016)]
Solvent |
SolvRho |
A |
B |
C |
D |
Gamma |
Benzene |
|
|
|
|||
Cyclohexane |
|
|
|
|||
DMSO |
|
|
|
-162.07 |
|
|
|
|
|
|
-0.33914 |
|
|
Water |
|
|
|
|
-21.405 |
|
 value from Ref. Kelly:2007.
value from Ref. Kelly:2007. Solvent |
SolvRho |
A |
B |
C |
D |
Gamma |
Benzene |
|
|
|
|||
Cyclohexane |
|
|
|
|||
DMSO |
|
|
|
-817.93 |
|
|
|
|
|
|
-0.44492 |
|
|
Water |
|
|
|
|
-30.503 |
|
 value from Ref. Kelly:2007.
value from Ref. Kelly:2007. The current implementation of CMIRS in Q-Chem computes the electrostatic energy using Chipman’s isodensity SS(V)PE module. The resulting isodensity cavity and the solute charge density are then employed in the calculation of the DEFESR interactions. To request a CMIRS calculation, users must set IDEFESR = 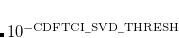 in an isodensity SS(V)PE calculation (see Section 12.2.5.2). The solvent-dependent empirical parameters A, B, C, D, Gamma in the CMIRS model need to be specified in the $pcm_nonels section. Three additional parameters are also required. One is the damping parameter Delta in the dispersion equation. We recommend the parameter fixed at
in an isodensity SS(V)PE calculation (see Section 12.2.5.2). The solvent-dependent empirical parameters A, B, C, D, Gamma in the CMIRS model need to be specified in the $pcm_nonels section. Three additional parameters are also required. One is the damping parameter Delta in the dispersion equation. We recommend the parameter fixed at  a.u. (about 3.7 Å), an optimized value that only considers dispersion at intermolecular distances larger than van der Waals contact distance. The second is solvent’s average electron density SolvRho. The last one is the number of Gauss–Laguerre points GauLag_N for the integration over the solvent region in the exchange equation. We recommend
a.u. (about 3.7 Å), an optimized value that only considers dispersion at intermolecular distances larger than van der Waals contact distance. The second is solvent’s average electron density SolvRho. The last one is the number of Gauss–Laguerre points GauLag_N for the integration over the solvent region in the exchange equation. We recommend  grid points for efficient integration with accuracy. Optimized parameters for the supported solvents are listed in Tables 12.4 and 12.5 for two different values of
grid points for efficient integration with accuracy. Optimized parameters for the supported solvents are listed in Tables 12.4 and 12.5 for two different values of  .[You and Herbert(2016)]
.[You and Herbert(2016)]
Example 12.292 CMIRS calculation for methane in the water solvent.
$rem
EXCHANGE = b3lyp5
BASIS = 6-31+g*
SCF_CONVERGENCE = 8
MEM_TOTAL = 4000
MEM_STATIC = 400
SYM_IGNORE = true
XC_GRID = 000096001202
$end
$molecule
0 1
C 0.000000 0.000005 0.000000
H 0.748558 0.801458 0.000000
H 0.506094 -0.972902 0.000000
H -0.627326 0.085706 0.895425
H -0.627326 0.085706 -0.895425
$end
@@@
$rem
EXCHANGE = b3lyp5
BASIS = 6-31+g*
SCF_CONVERGENCE = 8
MAX_SCF_CYCLES = 100
SOLVENT_METHOD = isosvp
SCF_GUESS = read
PCM_PRINT = 1
MEM_TOTAL = 4000
MEM_STATIC = 400
SVP_MEMORY = 1000
SYM_IGNORE = true
XC_GRID = 000096001202
$end
$molecule
read
$end
$svp
RHOISO=0.001, DIELST=78.36, NPTLEB=1202,
ITRNGR=2, IROTGR=2, IPNRF=1, IDEFESR=1
$end
$pcm_nonels
A -0.006736
B 0.032698
C -1249.6
D -21.405
Delta 7.0
Gamma 3.7
SolvRho 0.05
GauLag_N 40
$end
12.2.7 COSMO
According to Table 12.3, COSMO and C-PCM appear to differ only in the dielectric screening factor,  in Eq. eq:f_epsilon. Indeed, surface charges in either model are computed according to
in Eq. eq:f_epsilon. Indeed, surface charges in either model are computed according to
 |
(12.17) |
and as discussed in Section 12.2.3 the user has the option to choose either the original value suggested by Klamt,[Klamt and Schüürmann(1993), Klamt and Jonas(1996)]  , or else
, or else  as in, e.g., Refs. Truong:1995,Cossi:2003,Lange:2011. More importantly, however, COSMO differs from C-PCM in that the former includes a correction for outlying charge that goes beyond Eq. eq:C-PCM, whereas C-PCM consists of nothing more than induced surface charges computed (self-consistently) according to Eq. eq:C-PCM
as in, e.g., Refs. Truong:1995,Cossi:2003,Lange:2011. More importantly, however, COSMO differs from C-PCM in that the former includes a correction for outlying charge that goes beyond Eq. eq:C-PCM, whereas C-PCM consists of nothing more than induced surface charges computed (self-consistently) according to Eq. eq:C-PCM
Upon solution of Eq. eq:C-PCM, the outlying charge correction in COSMO[Klamt and Jonas(1996), Baldridge and Klamt(1997)] is obtained by first defining a larger cavity that is likely to contain essentially all of the solute’s electron density; in practice, this typically means using atomic radii of 1.95 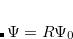 , where
, where 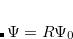 denotes the original atomic van der Waals radius that was used to compute
denotes the original atomic van der Waals radius that was used to compute  . (Note that unlike the PCMs described in Sections 12.2.2 and 12.2.3, where the atomic radii have default values but a high degree of user-controllability is allowed, the COSMO atomic radii are parameterized for this model and are fixed.) A new set of charges,
. (Note that unlike the PCMs described in Sections 12.2.2 and 12.2.3, where the atomic radii have default values but a high degree of user-controllability is allowed, the COSMO atomic radii are parameterized for this model and are fixed.) A new set of charges,  , is then computed on this larger cavity surface, and the charges on the original cavity surface are adjusted to new values,
, is then computed on this larger cavity surface, and the charges on the original cavity surface are adjusted to new values,  . Finally, a corrected electrostatic potential on the original surface is computed according to
. Finally, a corrected electrostatic potential on the original surface is computed according to  . It is this potential that is used to compute the solute–continuum electrostatic interaction (polarization energy),
. It is this potential that is used to compute the solute–continuum electrostatic interaction (polarization energy),  . (For comparison, when the C-PCM approach described in Section 12.2.2 is used, the electrostatic polarization energy is
. (For comparison, when the C-PCM approach described in Section 12.2.2 is used, the electrostatic polarization energy is  , computed using the original surface charges
, computed using the original surface charges  and surface electrostatic potential
and surface electrostatic potential  .) With this outlying charge correction, Q-Chem’s implementation of COSMO resembles the one in Turbomole.[Schäfer et al.(2000)Schäfer, Klamt, Sattle, Lohrenz, and Eckert]
.) With this outlying charge correction, Q-Chem’s implementation of COSMO resembles the one in Turbomole.[Schäfer et al.(2000)Schäfer, Klamt, Sattle, Lohrenz, and Eckert]
A COSMO calculation is requested by setting SOLVENT_METHOD = COSMO in the $rem section, in addition to normal job control variables. The keyword Dielectric in the $solvent section is used to set the solvent’s static dielectric constant, as described above for other solvation models. COSMO calculations can also be used as a starting point for COSMO-RS calculations,[Klamt et al.(2001)Klamt, Eckert, and Hornig, Klamt et al.(2010)Klamt, Eckert, and Arlt] where “RS” stands for “real solvent”. The COSMO-RS approach is not included in Q-Chem and requires the COSMOtherm program, which is licensed separately through COSMOlogic.[COS()] Q-Chem users who are interested in COSMOtherm can request special versions of Q-Chem for the generation of 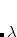 -surface files that are needed by COSMOtherm.
-surface files that are needed by COSMOtherm.
12.2.8 SM8, SM12, and SMD Models
The SM models developed by Cramer, Truhlar, and coworkers at the University of Minnesota are a class of implicit solvation models that are designed to be “universal” in the sense that they can be applied to any solvent for which a small of descriptors is known.[Cramer and Truhlar(2008)] (Note that the
models developed by Cramer, Truhlar, and coworkers at the University of Minnesota are a class of implicit solvation models that are designed to be “universal” in the sense that they can be applied to any solvent for which a small of descriptors is known.[Cramer and Truhlar(2008)] (Note that the  in SM
in SM is simply a version number; SM8, SM12, and SMD are available in Q-Chem.) In particular, the solvent descriptors are:
is simply a version number; SM8, SM12, and SMD are available in Q-Chem.) In particular, the solvent descriptors are:
dielectric constant
refractive index
bulk surface tension
acidity on the Abraham scale
basicity on the Abraham scale
carbon aromaticity, which equals the fraction of non-hydrogenic solvent atoms that are aromatic carbon atoms
electronegative halogenicity, which equals the fraction of non-hydrogenic solvent atoms that are F, Cl, or Br).
These models consist of a generalized Born treatment of continuum electrostatic interactions, along with non-electrostatic interactions that are parameterized in terms of atomic surface tensions. The non-electrostatic interactions include cavitation, dispersion, and changes in solvent structure, and the treatment of these non-electrostatic effects is crucial to obtaining accurate (free) energies of solvation.
12.2.8.1 The SM8 Model
The SM8 model is described in detail in Ref. Marenich:2007. It may be employed in conjunction with density functional theory (with any density functional available in Q-Chem) or with Hartree-Fock theory, but is intended for use only with the 6-31G*, 6-31+G*, and 6-31+G** basis sets, for reasons discussed below.
Bulk (continuum) electrostatic interactions in SM8 are described in terms of a generalized Born (GB) SCRF, using a solute cavity constructed from atom-centered spheres. For the atoms H, C, N, O, F, Si, P, S, Cl, and Br, atomic radii have been specifically optimized for use with SM8, whereas for other atoms the Bondi radius is used,[Bondi(1964)] or else a value of 2.0 Å for atoms not included in Bondi’s paper. Geometry-dependent radii are computed from these “intrinsic” Coulomb radii via a de-screening approximation.[Marenich et al.(2007)Marenich, Olson, Kelly, Cramer, and Truhlar]
In addition to GB electrostatics, there are several other contributions to the SM8 standard-state free energy of solvation. The first of these is called the electronic-nuclear-polarization (ENP) energy, or simply the electronic polarization (EP) energy if the solute geometry is assumed to be identical in the gas and solution phases. Another contribution to the free energy of solvation comes from short-range interactions with solvent molecules in the first solvation shell, and is sometimes called the cavitation/dispersion/solvent-structure (CDS) term. The CDS contribution to the solvation energy is a sum of terms that are each proportional (with geometry-dependent proportionality constants called atomic surface tensions) to the solvent-accessible surface areas (SASAs) of the individual solute atoms. The SASA of the solute molecule is the area of a surface generated by the center of a spherical effective solvent molecule rolling on the van der Waals surface of the solute molecule, as in the solvent-accessible surface that was mentioned in Section 12.2.2. The SASA is computed using the Analytic Surface Area (ASA) algorithm of Ref. Liotard:1995 and Bondi’s values for the van der Waals radii,[Bondi(1964)] or else a value of 2.0 Å if no Bondi radius is available. (Note that, as in the case of non-electrostatic interactions in PCMs, this means that a different molecular surface is used for the bulk electrostatics as compared to the non-electrostatic interactions.) The solvent probe radius used to generate the SASAs is set to 0.40 Å for all solvents. Note that the solvent-structure part of the CDS term includes many aspects of solvent structure that are not described by bulk electrostatics, for example, hydrogen bonding, exchange repulsion, and the variation of the effective dielectric constant in the first solvation shell, relative to its bulk value. The semi-empirical nature of the CDS term also makes up for errors due to ( ) assuming fixed and model-dependent values of the intrinsic Coulomb radii, and (
) assuming fixed and model-dependent values of the intrinsic Coulomb radii, and ( ) any systematic errors in the description of the solute–solvent electrostatic interactions using the GB approximation.
) any systematic errors in the description of the solute–solvent electrostatic interactions using the GB approximation.
The final component of the SM8 solvation free energy is the concentration component. This is zero if the standard-state concentration of the solute is the same in the gas and solution phases (e.g., if it is 1 mole/liter in the gas phase as well as in the solution). Otherwise, this correction can be computed using ideal gas formulas, as discussed below.
SM8 does not require the user to assign molecular mechanics atom types to atoms or groups; all atomic surface tensions in the theory are unique and continuous functions of the solute geometry, defined by the model and calculated internally within Q-Chem. In principle, SM8 can be used with any level of electronic structure theory so long as accurate partial charges can be computed, but Q-Chem’s implementation of SM8 specifically uses self-consistently polarized Charge Model 4 (CM4) class IV charges.[Kelly et al.(2005)Kelly, Cramer, and Truhlar] CM4 charges are obtained from Löwdin population analysis charges, via a mapping whose parameters depend on the basis set (and only on the basis set, not on the density functional or anything else). Basis sets supported for SM8 calculations in Q-Chem are:
6-31G*
6-31+G*
6-31+G**
The charge mapping parameters are given in Ref. Kelly:2005. Other basis sets should not be used in SM8 calculations.
The SM8 solvation free energy is output at  K for a standard-state concentration of 1 M in both the gas and solution phase. However, solvation free energies in the literature are often tabulated using a standard state of
K for a standard-state concentration of 1 M in both the gas and solution phase. However, solvation free energies in the literature are often tabulated using a standard state of  atm for the gase. To convert 1 M-to1 M solvation free energies at 298 K to a standard state consisting of
atm for the gase. To convert 1 M-to1 M solvation free energies at 298 K to a standard state consisting of  atm for the gas and a 1 M concentration in solution, add
atm for the gas and a 1 M concentration in solution, add  kcal/mol to the computed solvation free energy.
kcal/mol to the computed solvation free energy.
Solution-phase geometry optimizations can be carried out, but basis sets that use spherical harmonic  functions, or angular momentum higher than
functions, or angular momentum higher than  (
( ,
,  , etc.) are not supported. Since, by definition, the 6-31G*, 6-31+G*, and 6-31+G** basis sets have Cartesian
, etc.) are not supported. Since, by definition, the 6-31G*, 6-31+G*, and 6-31+G** basis sets have Cartesian  shells, they are examples of basis sets that may be used for geometry optimization with SM8. Solution-phase Hessian calculations can be carried out by numerical differentiation of analytical energy gradients or by double differentiation of energies, although the former procedure is both more stable and more economical. The analytic gradients of SM8 are based on the analytical derivatives of the polarization free energy and the analytical derivatives of the CDS terms derived in Ref. Zhu:1999.
shells, they are examples of basis sets that may be used for geometry optimization with SM8. Solution-phase Hessian calculations can be carried out by numerical differentiation of analytical energy gradients or by double differentiation of energies, although the former procedure is both more stable and more economical. The analytic gradients of SM8 are based on the analytical derivatives of the polarization free energy and the analytical derivatives of the CDS terms derived in Ref. Zhu:1999.
An SM8 calculation is requested by setting SOLVENT_METHOD = SM8 in the $rem section, along with other job-control variables appropriate for a Hartree-Fock or DFT calculation. Additional variables for SM calculations should be listed in a $smx input section; for SM8, the only additional variable that is required is the name of the solvent:
calculations should be listed in a $smx input section; for SM8, the only additional variable that is required is the name of the solvent:
Solvent
Sets the SM
solvent
INPUT SECTION: $smx
TYPE:
STRING
DEFAULT:
water
OPTIONS:
Any name from the list of solvents given below.
RECOMMENDATION:
NONE
1,1,1-trichloroethane |
bromoethane |
|
1,1,2-trichloroethane |
bromooctane |
|
1,1-dichloroethane |
butanal |
|
1,2,4-trimethylbenzene |
butanoicacid |
|
1,4-dioxane |
butanone |
|
1-bromo-2-methylpropane |
butanonitrile |
|
1-bromopentane |
butylethanoate |
|
1-bromopropane |
butylamine |
|
1-butanol |
butylbenzene |
|
1-chloropentane |
carbon disulfide |
heptane |
1-chloropropane |
carbon tetrachloride |
hexadecane |
1-decanol |
chlorobenzene |
hexane |
1-fluorooctane |
chlorotoluene |
nitrobenzene |
1-heptanol |
|
nitroethane |
1-hexanol |
decalin |
nitromethane |
1-hexene |
cyclohexane |
methylaniline |
1-hexyne |
cyclohexanone |
nonane |
1-iodobutane |
cyclopentane |
octane |
1-iodopentene |
cyclopentanol |
pentane |
1-iodopropane |
cyclopentanone |
|
1-nitropropane |
decane |
|
1-nonanol |
dibromomethane |
|
1-octanol |
dibutyl ether |
|
1-pentanol |
dichloromethane |
|
1-pentene |
diethyl ether |
pentadecane |
1-pentyne |
diethylsulfide |
pentanal |
1-propanol |
diethylamine |
pentanoic acid |
2,2,20trifluoroethanol |
diiodomethane |
pentylethanoate |
2,2,4-trimethylpentane |
dimethyldisulfide |
pentylamine |
2,4-dimethylpentane |
dimethylacetamide |
perfluorobenzene |
2,4-dimethylpyridine |
dimethylformamide |
phenyl ether |
2,6-dimethylpyridine |
dimethylpyridine |
propanal |
2-bromopropane |
dimethyl sulfoxide |
propanoic acid |
2-chlorobutane |
dipropylamine |
propanonitrile |
2-heptanone |
dodecane |
propylethanoate |
2-hexanone |
|
propylamine |
2-methylpentane |
|
|
2-methylpyridine |
ethanethiol |
pyridine |
2-nitropropane |
ethanol |
pyrrolidine |
2-octanone |
ethylethanoate |
|
2-pentanone |
ethylmethanoate |
|
2-propanol |
ethylphenyl ether |
|
2-propen-1-ol |
ethylbenzene |
tetrachloroethene |
3-methylpyridine |
ethylene glycol |
tetrahydrofuran |
3-pentanone |
fluorobenzene |
tetrahyrothiophenedioxide |
4-heptanone |
formamide |
tetralin |
4-methyl-2-pentanone |
formic acid |
thiophene |
4-methylpyridine |
hexadecyliodide |
thiophenol |
5-nonanone |
hexanoic acid |
toluene |
acetic acid |
iodobenzene |
|
acetone |
iodoethane |
tribromomethane |
acetonitrile |
iodomethane |
tributylphosphate |
aniline |
isobutanol |
trichloroethene |
anisole |
isopropyl ether |
trichloromethane |
benzaldehyde |
isopropylbenzene |
triethylamine |
benzene |
isopropyltoluene |
undecane |
benzonitrile |
|
water |
benzyl alcohol |
mesitylene |
|
bromobenzene |
methanol |
other |
The final choice, Solvent = “other”, requires an additional free-format file called “solvent_data” that should contain the float-point values of the following solvent descriptors:
Dielec |
dielectric constant, |
SolN |
index of refraction at optical frequencies at 293 K, |
SolA |
Abraham’s hydrogen bond acidity, |
SolB |
Abraham’s hydrogen bond basicity, |
SolG |
|
interface at 298 K, and |
|
SolC |
aromaticity, |
carbon atoms |
|
SolH |
electronegative “halogenicity”, |
F, Cl or Br |
For a desired solvent, these values can be derived from experiment or from interpolation or extrapolation of data available for other solvents. Solvent parameters for common organic solvents are tabulated in the Minnesota Solvent Descriptor Database. The latest version of this database is available at:
The SM8 test suite contains the following representative examples:
single-point solvation energy and analytical gradient calculation for 2,2-dichloroethenyl dimethyl phosphate in water at the M06-2X/6-31G* level;
single-point solvation energy calculation for 2,2-dichloroethenyl dimethyl phosphate in benzene at the M06-2X/6-31G* level;
single-point solvation energy calculation for 2,2-dichloroethenyl dimethyl phosphate in ethanol at the M06-2X/6-31G* level;
single-point solvation energy calculation for 5-fluorouracil in water at the M06/6-31+G* level;
single-point solvation energy calculation for 5-fluorouracil in octanol at the M06-L/6-31+G* level;
single-point solvation energy and analytical gradient calculation for 5-fluorouracil in fluorobenzene at the M06-HF/6-31+G** level;
geometry optimization for protonated methanol
 in water at the B3LYP/6-31G* level;
in water at the B3LYP/6-31G* level; finite-difference frequency (with analytical gradient) calculation for protonated methanol
 in water at the B3LYP/6-31G* level.
in water at the B3LYP/6-31G* level.
Users who wish to calculate solubilities can calculate them from the free energies of solvation by the method described in Ref. Thompson:2003. The present model can also be used with confidence to calculate partition coefficients (e.g., Henry’s Law constants, octanol/water partition coefficients, etc.) by the method described in Ref. Cramer:2001.
The user should note that the free energies of solvation calculated by the SM8 model in the current version of Q-Chem are all what may be called equilibrium free energies of solvation. The nonequilibrium algorithm required for vertical excitation energies[Li et al.(2000)Li, Cramer, and Truhlar] is not yet available in Q-Chem. (Nonequilibrium versions of PCMs are available instead; see Section 12.2.2.3.)
12.2.8.2 The SM12 Model
The SM12 model[Marenich et al.(2013)Marenich, Cramer, and Truhlar] is also available in Q-Chem. Similar to SM8, it employs (a) the generalized Born approximation for the bulk electrostatic contribution to the free energy of solvation, and (b) the same formulas (with re-optimized parameters) for CDS contributions. SM12 holds several advantages over SM8, and perhaps foremost among these is that it uses CM5 charges,[Marenich et al.(2012)Marenich, Jerome, Cramer, and Truhlar] which are based on Hirshfeld population analysis, or else charges derived from the electrostatic potential,[Singh and Kollman(1986), Breneman and Wiberg(1990)] for the bulk electrostatics term. These charges are stable with respect to extension of the basis set, and thus SM12 can be used with larger basis sets whereas SM8 is limited to 6-31G*, 6-31+G*, and 6-31+G**, due to instabilities in the Löwdin charges in larger basis sets. In addition, SM12 is parameterized using a more diverse training set as compared to SM8, and is defined for the entire periodic table. However, the SM12 analytic gradient is not available in Q-Chem at present.
An SM12 calculation is requested by setting SOLVENT_METHOD = SM12 in the $rem section. The manner in which the electrostatic term is computed is controlled by the Charges keyword in the $smx input section.
Charges
Sets the type of atomic charges for the SM12 electrostatic term.
INPUT SECTION: $smx
TYPE:
STRING
DEFAULT:
CM5
OPTIONS:
CM5
Charge Model 5 charges[Marenich et al.(2012)Marenich, Jerome, Cramer, and Truhlar]
MK
Merz-Singh-Kollman charges[Singh and Kollman(1986)]
CHELPG
ChElPG charges[Breneman and Wiberg(1990)]
RECOMMENDATION:
None. Merz-Singh-Kollman and ChElPG charges are fit to reproduce the molecular electrostatic potential on the van der Waals surface or on a cubic grid, respectively, whereas CM5 is an empirical model based on Hirshfeld population analysis.
Example 12.293 SM12CM5 calculation of the solvation free energy of water in the 1-octanol solvent.
$molecule
0 1
O 0.000000 0.125787 0.000000
H 0.758502 -0.503148 0.000000
H -0.758502 -0.503148 0.000000
$end
$rem
SCF_GUESS core
METHOD b3lyp
BASIS 6-31G*
SYM_IGNORE true
SOLVENT_METHOD sm12
$end
$smx
solvent 1octanol
charges chelpg
$end
12.2.8.3 The SMD Model
The SMD model[Marenich et al.(2009)Marenich, Olson, Kelly, Cramer, and Truhlar] is also available in Q-Chem. Within this model, the electrostatic contribution to the free energy solvation is described via the IEF-PCM model, where the CDS contributions follow the formulas as SM8 and SM12 with the parameters re-optimized to be compatible with the IEF-PCM electrostatics. Relative to SM8 or SM12, where the electrostatic interactions are defined in terms of atomic point charges that are sensitive to the choice of basis set (and therefore only certain basis sets are supported for use with these models), SMD can be used with any basis set.
An SMD energy or gradient calculation is requested by setting SOLVENT_METHOD = SMD in the $rem section. While Q-Chem users can vary the parameters for the IEF-PCM part of the SMD calculation, this should be done with caution because a modified IEF-PCM electrostatics might be less compatible with CDS parameters and thus lead to less accurate results.
Example 12.294 SMD force calculation for tetrahydrofuran (THF) in the pentane solvent.
$molecule
0 1
C -0.361658 -0.986967 0.222366
C -1.331098 0.144597 -0.108363
O -0.592574 1.354183 0.036738
C 0.798089 1.070899 0.136509
C 0.964682 -0.396154 -0.256319
H -0.625676 -1.925862 -0.267011
H -0.333229 -1.158101 1.302753
H -1.697529 0.068518 -1.140448
H -2.193412 0.181620 0.562129
H 1.130199 1.238399 1.169839
H 1.348524 1.754318 -0.514697
H 1.050613 -0.489646 -1.343151
H 1.843065 -0.855802 0.199659
$end
$rem
JOBTYPE force
METHOD b3lyp
BASIS 6-31G*
SOLVENT_METHOD smd
$end
$smx
solvent pentane
$end
12.2.9 Langevin Dipoles Model
Q-Chem provides the option to calculate molecular properties in aqueous solution and the magnitudes of the hydration free energies by the Langevin dipoles (LD) solvation model developed by Jan Florián and Arieh Warshel[Florián and Warshel(1997), Florián and Warshel(1999)] at the University of Southern California. In this model, a solute molecule is surrounded by a sphere of point dipoles, with centers on a cubic lattice. Each of these “Langevin” dipoles changes its size and orientation in the electrostatic field of the solute and the other Langevin dipoles. The electrostatic field from the solute is determined rigorously by the integration of its charge density, whereas for dipole–dipole interactions, a 12 Å cutoff is used. The Q-Chem/ChemSol 1.0 implementation of the LD model is fully self-consistent in that the molecular quantum mechanical calculation takes into account solute–solvent interactions. Further details on the implementation and parameterization of this model can be found in the literature.[Florián and Warshel(1997), Florián and Warshel(1999)]
The results of ChemSol calculations are printed in the standard output file. Below is a part of the output for a calculation on the methoxide anion (corresponding to the sample input given later on, and the sample file in the $QC/samples directory).
Energy Component |
Value / kcal mol |
LD Electrostatic energy |
|
Hydrophobic energy |
0.28 |
van der Waals energy |
|
Bulk correction |
|
Solvation free energy, |
|
The total hydration free energy,  (ILD) is calculated as a sum of several contributions. Note that the electrostatic part of
(ILD) is calculated as a sum of several contributions. Note that the electrostatic part of  is calculated by using the linear-response approximation[Florián and Warshel(1997)] and contains contributions from the polarization of the solute charge distribution due to its interaction with the solvent. This results from the self-consistent implementation of the Langevin dipoles model within Q-Chem.
is calculated by using the linear-response approximation[Florián and Warshel(1997)] and contains contributions from the polarization of the solute charge distribution due to its interaction with the solvent. This results from the self-consistent implementation of the Langevin dipoles model within Q-Chem.
To perform an LD calculation in Q-Chem, specify normal job-control variables for a Hartree-Fock or DFT calculation, and set SOLVENT_METHOD = CHEM_SOL in the $rem section. Additional fine-tuning is accomplished using a set of keywords in a $chem_sol input section. The remainder of this section summarizes these keywords.
EField
Determines how the solute charge distribution is approximated in evaluating the electrostatic field of the solute.
INPUT SECTION: $chem_sol
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
1
Exact solute charge distribution is used.
0
Solute charge distribution is approximated by Mulliken atomic charges.
RECOMMENDATION:
None. The Mulliken-based procedure is faster but less rigorous.
NGrids
Sets the number of grids used to calculate the average hydration free energy.
INPUT SECTION: $chem_sol
TYPE:
INTEGER
DEFAULT:
5
will be averaged over 5 different grids.
OPTIONS:

Use
different grids.
RECOMMENDATION:
None. The maximum allowed value of
is 20.
Controls printing in the ChemSol part of the Q-Chem output file.
INPUT SECTION: $chem_sol
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Limited printout
1
Full printout
RECOMMENDATION:
None.
ReadRadii
Read user-defined atomic radii from section $van_der_waals.
INPUT SECTION: $chem_sol
TYPE:
None
DEFAULT:
Off
OPTIONS:
No options. Specify the keyword to use user-defined atomic radii.
RECOMMENDATION:
None.
Accurate calculations of hydration free energies require a judicious choice of the solute–solvent boundary in terms of atom-type dependent parameters. The default atomic van der Waals radii available in Q-Chem were chosen to provide reasonable hydration free energies for most solutes and basis sets. These parameters basically coincide with the ChemSol 2.0 radii given in Ref. Florian:1999. The only difference between the Q-Chem and ChemSol 2.0 atomic radii stems from the fact that Q-Chem parameter set uses radii for carbon and oxygen that are independent of the atom’s hybridization state. User-defined atomic radii can be specified by declaring the option ReadRadii in the $chem_sol input section, and then placing the radii in the $van_der_waals section. Two different (and mutually exclusive) formats can be used, as shown below.
$van_der_waals
1
atomic_number vdW_radius
...
$end
$van_der_waals
2
sequential_atom_number vdW_radius
...
$end
The purpose of the second format is to permit the user to customize the radius of specific atoms, in the order that they appear in the $molecule section, rather than simply by atomic numbers as in format 1. The radii of atoms that are not listed in the $van_der_waals input will be assigned default values. The atomic radii that were used in the calculation are printed in the ChemSol part of the output file in the column denoted rp. All radii should be given in Ångstroms.
Example 12.295 A Langevin dipoles calculation on the methoxide anion. A customized value is specified for the radius of the C atom.
$molecule
-1 1
C 0.0000 0.0000 -0.5274
O 0.0000 0.0000 0.7831
H 0.0000 1.0140 -1.0335
H 0.8782 -0.5070 -1.0335
H -0.8782 -0.5070 -1.0335
$end
$rem
METHOD hf
BASIS 6-31G
SCF_CONVERGENCE 6
SOLVENT_METHOD Chem_Sol
$end
$chem_sol
ReadRadii
$end
$van_der_waals
2
1 2.5
$end
12.2.10 Poisson Boundary Conditions
Each of the implicit solvation models described above is designed for isotropic, bulk solvation—conditions that can be qualitatively described using a scalar dielectric constant,  . For an anisotropic environment, such as a liquid/vapor interface, a more general approach is to solve Poisson’s equation with a spatially-varying dielectric function,
. For an anisotropic environment, such as a liquid/vapor interface, a more general approach is to solve Poisson’s equation with a spatially-varying dielectric function,  . Such an approach can be used, for example, to model the air/water interface by describing certain regions of space using
. Such an approach can be used, for example, to model the air/water interface by describing certain regions of space using  (air) and other regions using
(air) and other regions using  (water).[Coons et al.(2016)Coons, You, and Herbert, Coons and Herbert(2018)] The atomistic region is described at the SCF level. Construction of the dielectric function
(water).[Coons et al.(2016)Coons, You, and Herbert, Coons and Herbert(2018)] The atomistic region is described at the SCF level. Construction of the dielectric function  is based on a solute cavity, somewhat analogous to the solute cavity in a PCM calculation but where the dielectric changes smoothly (rather than abruptly) from
is based on a solute cavity, somewhat analogous to the solute cavity in a PCM calculation but where the dielectric changes smoothly (rather than abruptly) from  inside the cavity (in the atomistic QM region) to
inside the cavity (in the atomistic QM region) to  outside, in the continuum solvent. Options for modeling a liquid/vapor interface are also available; see Section 12.2.10.3. In contrast to PCMs, which must approximate the “volume polarization” due to penetration of the tails of the QM charge density beyond the solute cavity, this effect is described exactly under Poisson boundary conditions. The price to be paid for lifting this approximation is that charge densities must be discretized and integrated over three-dimensional space rather than simply a two-dimensional solute cavity surface.
outside, in the continuum solvent. Options for modeling a liquid/vapor interface are also available; see Section 12.2.10.3. In contrast to PCMs, which must approximate the “volume polarization” due to penetration of the tails of the QM charge density beyond the solute cavity, this effect is described exactly under Poisson boundary conditions. The price to be paid for lifting this approximation is that charge densities must be discretized and integrated over three-dimensional space rather than simply a two-dimensional solute cavity surface.
Q-Chem’s implementation of Poisson boundary conditions was introduced in Ref. Coons:2016 and refined in Ref. Coons:2018. Users of this methodology are asked to cite at least Ref. Coons:2018.
12.2.10.1 Theory
The most general formulation of Poisson’s equation, for a dielectric function rather than a dielectric constant, is
![\begin{equation} \label{eq:Poisson} \hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }}\bm@general \boldmath \m@ne \mv@bold \bm@command {\cdot }\left[ \varepsilon (\mathbf{r}) \hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }}\varphi _{\rm tot}(\mathbf{r}) \right] = - 4\pi \rho _{\rm sol}(\mathbf{r}) \; . \end{equation}](images/img-2084.png) |
(12.18) |
The solute’s charge density will be separated into nuclear and electronic components,
 |
(12.19) |
The total electrostatic potential  is comprised of the solute’s electrostatic potential
is comprised of the solute’s electrostatic potential  , which is obtained from the density in Eq. eq:rho, plus the polarization potential induced in the medium:
, which is obtained from the density in Eq. eq:rho, plus the polarization potential induced in the medium:
 |
(12.20) |
To compute  , the electronic contribution to the electrostatic potential in vacuum is first evaluated on a Cartesian grid,
, the electronic contribution to the electrostatic potential in vacuum is first evaluated on a Cartesian grid,
 |
(12.21) |
Here P is the one-electron density matrix,  and
and  are atom-centered Gaussian basis functions, and the integration is over
are atom-centered Gaussian basis functions, and the integration is over 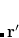 . The electronic part of the solute’s charge density is then obtained from
. The electronic part of the solute’s charge density is then obtained from
 |
(12.22) |
where in practice the Laplacian of  is evaluated using an eighth-order finite difference scheme.[Coons and Herbert(2018)] The nuclear charge density
is evaluated using an eighth-order finite difference scheme.[Coons and Herbert(2018)] The nuclear charge density  is described classically,
is described classically,
 |
(12.23) |
but to avoid numerical problems the nuclear charges are smeared out over one Cartesian grid voxel in practice. Operationally, this is achieved by adding  to the grid point nearest
to the grid point nearest 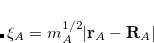 , where
, where  is the volume of a Cartesian voxel. The exact nuclear electrostatic potential in vacuum is computed according to
is the volume of a Cartesian voxel. The exact nuclear electrostatic potential in vacuum is computed according to
 |
(12.24) |
The Dirac delta function in Eq. eq:rho_nuc has dimensions of (volume)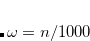 and therefore incorporates the aforementioned factor of
and therefore incorporates the aforementioned factor of 
Having computed the electronic and nuclear charge densities and the electrostatic potentials in vacuum, one has in hand an exact solution of Eq. eq:Poisson for the case where  . The induced polarization charge density and corresponding electrostatic potential are then obtained iteratively, following closely the procedure outlined in Refs. Fisicaro:2016 and Andreussi:2012. Equation eq:Poisson is rewritten to appear as Poisson’s equation in vacuum with an additional source charge density:
. The induced polarization charge density and corresponding electrostatic potential are then obtained iteratively, following closely the procedure outlined in Refs. Fisicaro:2016 and Andreussi:2012. Equation eq:Poisson is rewritten to appear as Poisson’s equation in vacuum with an additional source charge density:
![$\displaystyle \label{eq:Poisson2} \begin{aligned} \hat{\nabla }^{2} \varphi _{\rm tot}(\mathbf{r}) & = -4\pi \left[\frac{\rho _{\rm sol}(\mathbf{r})}{\varepsilon (\mathbf{r})} + \frac{\hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }} \ln \varepsilon (\mathbf{r}) \bm@general \boldmath \m@ne \mv@bold \bm@command {\cdot } \hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }} \varphi _{\rm tot}(\mathbf{r})}{4\pi } \right] \\ & = -4\pi \bigl [ \rho _{\rm sol}(\mathbf{r}) + \rho _{\rm pol}(\mathbf{r}) \bigr ] \; , \end{aligned} $](images/img-2102.png) |
(12.25) |
where the polarization charge density is
 |
(12.28) |
The iterative charge density  takes the form
takes the form
 |
(12.29) |
at iteration  . This function is nonzero only in transition regions where the dielectric is being interpolated from vacuum to solvent. Note also that the second term in Eq. eq:rho_pol vanishes wherever
. This function is nonzero only in transition regions where the dielectric is being interpolated from vacuum to solvent. Note also that the second term in Eq. eq:rho_pol vanishes wherever  . The quantity
. The quantity  is iterated to convergence by performing updates
is iterated to convergence by performing updates  using Eq. eq:rho_iter1, taking
using Eq. eq:rho_iter1, taking  to be the solute’s electrostatic potential in vacuum. Each time
to be the solute’s electrostatic potential in vacuum. Each time  is updated, a new polarization charge density is generated and Eq. eq:Poisson2 is solved to obtain a new total electrostatic potential. To stabilize the iterative updates of
is updated, a new polarization charge density is generated and Eq. eq:Poisson2 is solved to obtain a new total electrostatic potential. To stabilize the iterative updates of  , we use a damping procedure
, we use a damping procedure
![$\displaystyle \label{eq:rho_ iter2} \begin{aligned} \rho _{\rm iter}^{(k+1)}(\mathbf{r}) & = \frac{\eta }{4\pi } \bigl [\hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }} \ln \varepsilon (\mathbf{r})\bm@general \boldmath \m@ne \mv@bold \bm@command {\cdot } \hat{\bm@general \boldmath \m@ne \mv@bold \bm@command {\nabla }} \varphi ^{(k)}_{\rm tot}(\mathbf{r})\bigr ] + (1- \eta ) \rho _{\rm iter}^{(k)}(\mathbf{r}) \\ & = \eta \rho _{\rm iter}^{(k+1)} + (1- \eta ) \rho _{\rm iter}^{(k)}(\mathbf{r}) \end{aligned} $](images/img-2111.png) |
(12.30) |
rather than using Eq. eq:rho_iter1 as written. Following Refs. Fisicaro:2016 and Andreussi:2012, we use  .
.
Once the total charge density and electrostatic potential are iterated to self-consistency, the free energy of solvation,
 |
(12.33) |
is computed, where
 |
(12.34) |
Since  and
and  are computed self-consistently at each SCF iteration, the polarization effects must be incorporated into the Fock matrix. This is accomplished by adding the correction term
are computed self-consistently at each SCF iteration, the polarization effects must be incorporated into the Fock matrix. This is accomplished by adding the correction term  . The matrix form of this correction in the atomic orbital basis is
. The matrix form of this correction in the atomic orbital basis is
 |
(12.35) |
For additional details and a full description of the algorithm, see Ref. Coons:2018.
12.2.10.2 Nonequilibrium Solvation for Vertical Ionization
Nonequilibrium solvation within the framework of PCMs is discussed in Section 12.2.2.3, and that methodology[Mewes et al.(2015a)Mewes, You, Wormit, Kriesche, Herbert, and Dreuw, You et al.(2015)You, Mewes, Dreuw, and Herbert] has been adapted for vertical ionization processes in conjunction with Poisson boundary conditions.[Coons et al.(2016)Coons, You, and Herbert, Coons and Herbert(2018)] A state-specific approach has been implemented that requires solution of a nonlinear Schrödinger equation, Eq. eq:SS-sdeq. For the reference state, corresponding to  in Eq. eq:SS-sdeq, this is equivalent to solving Eq. eq:Poisson for the induced polarization potential and computing the solvation free energy and Fock matrix correction according to Eqs. eq:Gpol and eq:fock, respectively. For the ionized state, denoted by a subscript
in Eq. eq:SS-sdeq, this is equivalent to solving Eq. eq:Poisson for the induced polarization potential and computing the solvation free energy and Fock matrix correction according to Eqs. eq:Gpol and eq:fock, respectively. For the ionized state, denoted by a subscript  , the solvent polarization is partitioned into fast and slow components. Within the Marcus partitioning scheme,[You et al.(2015)You, Mewes, Dreuw, and Herbert] Eq. eq:Poisson2 becomes[Coons and Herbert(2018)]
, the solvent polarization is partitioned into fast and slow components. Within the Marcus partitioning scheme,[You et al.(2015)You, Mewes, Dreuw, and Herbert] Eq. eq:Poisson2 becomes[Coons and Herbert(2018)]
 |
(12.36) |
where the fast polarization charge density of the ionized state,  , is given by
, is given by
![\begin{equation} \label{eq:rho_ pol_ neq1} \rho ^{\rm fast}_{{\rm pol}, i}(\mathbf{r}) = \rho ^{}_{{\rm iter}, i}(\mathbf{r}) + \left(\frac{1-\varepsilon _{\rm opt}(\mathbf{r})}{\varepsilon _{\rm opt}(\mathbf{r})}\right) \bigl [ \rho ^{}_{{\rm sol}, i}(\mathbf{r}) + \rho ^{\rm slow}_{{\rm pol}, 0}(\mathbf{r}) \bigr ] \end{equation}](images/img-2122.png) |
(12.37) |
and the fast polarization potential,  , is
, is
 |
(12.38) |
Subscripts  and 0 refer to the ionized state and the reference state, respectively. The quantity
and 0 refer to the ionized state and the reference state, respectively. The quantity  in Eq. eq:rho_pol_neq1 is the solvent’s optical dielectric constant, and
in Eq. eq:rho_pol_neq1 is the solvent’s optical dielectric constant, and  is computed using Eq. eq:rho_iter2 but with a dielectric function constructed using
is computed using Eq. eq:rho_iter2 but with a dielectric function constructed using  and with
and with  substituted in place of
substituted in place of  . For the Marcus partitioning scheme, the slow component of the induced solvent polarization charge density is computed as the three-dimensional (volume charge rather than surface charge) analogue of Eq. slow_q.
. For the Marcus partitioning scheme, the slow component of the induced solvent polarization charge density is computed as the three-dimensional (volume charge rather than surface charge) analogue of Eq. slow_q.
12.2.10.3 Job Control for the Poisson Equation Solver
A calculation using Poisson boundary conditions is requested by setting SOLVE_PEQ = TRUE in the $rem section. For computational efficiency, solvent effects from the Poisson equation solver are not incorporated until the error in the vacuum SCF calculation falls below a specified threshold, taken to be 10 a.u. by default and controllable using the $rem variable PEQ_SWITCH.
a.u. by default and controllable using the $rem variable PEQ_SWITCH.
Note: When SOLVE_PEQ = TRUE, the keywords SYM_IGNORE and NO_REORIENT are also set to TRUE. Poisson’s equation is discretized on a three-dimensional grid and the energy need not be rotationally invariant unless the grid spacing is sufficiently small.
SOLVE_PEQ
Perform a solvation free energy calculation on a Cartesian grid using Poisson equation boundary conditions.
TYPE:
STRING
DEFAULT:
False
OPTIONS:
TRUE/FALSE
RECOMMENDATION:
None.
PEQ_SWITCH
Inclusion of solvent effects begins when the SCF error falls below 10
.
TYPE:
INTEGER
DEFAULT:
3
OPTIONS:

Corresponding to 10
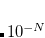
RECOMMENDATION:
Use the default unless solvent effects need to be incorporated earlier in the SCF procedure.
Further job control for the Poisson equation solver (PEqS) routines is set up in two sections: $peqs_grid and $peqs. The former is used to define the Cartesian discretization grid, as follows:
The Cartesian grid must be orthorhombic and Nx, Ny, and Nz refer to the number of grid points for the
$peqs_grid
DimX <Nx> <Xmin> <Xmax>
DimY <Ny> <Ymin> <Ymax>
DimZ <Nz> <Zmin> <Zmax>
$end
 ,
,  , and
, and  axes.
axes.
Note: A fourth-order multigrid algorithm is used to accelerate convergence of the conjugate gradient PEqS routine that solves Eq. eq:Poisson2.[Coons and Herbert(2018)] This requires that the number of grid points be odd, with the additional constraint that the quantities  ,
,  , and
, and  must all be divisible by 8.
must all be divisible by 8.
Values in the last two columns of the $peqs_grid section specify the minimum and maximum values of  ,
,  , and
, and  , in units of Ångstroms. The length of the grid in the
, in units of Ångstroms. The length of the grid in the  direction is
direction is  and the grid spacing is
and the grid spacing is  . The volume element discussed in the context of Eq. eq:rho_nuc is
. The volume element discussed in the context of Eq. eq:rho_nuc is  .
.
The $peqs section controls other aspects of a PEqS calculation, including construction of the solute cavity and other required parameters for interfacial or nonequilibrium solvation. The format is:
Available keywords are described below.
$peqs
<Keyword> <parameter/option>
$end
PEQMaxIter
Sets the maximum number of iterations used in the conjugate gradient solver.
INPUT SECTION: $peqs
TYPE:
INTEGER
DEFAULT:
500
OPTIONS:
User-defined.
RECOMMENDATION:
Use the default unless the calculation fails to converge.
PEQSolverThresh
The electrostatic potential is considered converged when the error falls below 10
.
INPUT SECTION: $peqs
TYPE:
INTEGER
DEFAULT:
5
OPTIONS:

Corresponding to 10
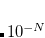
RECOMMENDATION:
Use the default unless a tighter convergence criterion is desired, at greater computational cost.
PolarIterScale
Specifies the mixing parameter
that is used in Eq. eq:rho_iter2 to stabilize iterative solution for the polarization charge density.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
0.6
OPTIONS:

Desired value of the mixing parameter (unit-less).
RECOMMENDATION:
Use the default, which was tested in Refs. Fisicaro:2016 and Andreussi:2012, unless the calculation proves difficult to converge.
BatchSize
Evaluate electrostatic potential integrals in batches over small parts of the Cartesian grid, rather than computing all integrals in a single batch.
INPUT SECTION: $peqs
TYPE:
INTEGER
DEFAULT:
5000
OPTIONS:

Corresponding to a batch size of
grid points.
RECOMMENDATION:
For large grids (
grid points), a batch size
is recommended.
SolventDielectric
Sets the dielectric value for the solvent.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
78.39
OPTIONS:

Desired value of
(dimensionless).
RECOMMENDATION:
The default value corresponds to water at 25
C.
OpticalDielectric
Sets the optical dielectric value of the solvent.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
1.7778
OPTIONS:

Desired value of
(dimensionless).
RECOMMENDATION:
The optical dielectric is equal to the square of the index of refraction. The default value corresponds to water at 25
C.
SoluteCavity
Specifies the type of solute cavity, which determines the form of the dielectric function
.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
Vacuum
OPTIONS:
Vacuum
Perform calculation in vacuum,
.
RigidVDW
Create a cavity using spherically symmetric error functions.
Spherical
Create a single spherical cavity around the solute.
RECOMMENDATION:
None.
In conventional PCMs the solute cavity is a rigid two-dimensional surface constructed from a union of atomic spheres, the radii of which are generally take to be equal to the van der Waals radius ( ) scaled by a factor of 1.2; see Section 12.2.3.[Herbert and Lange(2016)] This cavity is rigid in the sense that once the atomic coordinates are specified, it remains unchanged during the SCF cycles. (The isodensity cavity discussed in Section 12.2.5 is an exception, but is not available for the PEqS method.) Furthermore, there is an abrupt and discontinuous change in the dielectric constant at the solute/continuum boundary. A three-dimensional analogue of this cavity, using continuous and differentiable spherically-symmetric error functions, has been implemented for PEqS calculations, following the procedure in Ref. Fisicaro:2016. The dielectric function, which depends parameterically on the nuclear positions
) scaled by a factor of 1.2; see Section 12.2.3.[Herbert and Lange(2016)] This cavity is rigid in the sense that once the atomic coordinates are specified, it remains unchanged during the SCF cycles. (The isodensity cavity discussed in Section 12.2.5 is an exception, but is not available for the PEqS method.) Furthermore, there is an abrupt and discontinuous change in the dielectric constant at the solute/continuum boundary. A three-dimensional analogue of this cavity, using continuous and differentiable spherically-symmetric error functions, has been implemented for PEqS calculations, following the procedure in Ref. Fisicaro:2016. The dielectric function, which depends parameterically on the nuclear positions 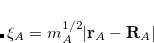 , is
, is
 |
(12.39) |
where
![\begin{equation} \label{eq:h_ func} h(d_{A}, \Delta ;\lvert \mathbf{r} - \mathbf{R}_{A} \rvert ) = \frac{1}{2} \left[ 1 + {\rm erf} \left(\frac{\lvert \mathbf{r} - \mathbf{R}_{A} \rvert - d_{A}}{\Delta } \right) \right] \; . \end{equation}](images/img-2142.png) |
(12.40) |
Equation eq:rigidvdw smoothly interpolates between  and
and  , over a length scale of
, over a length scale of  . The value of
. The value of  is specified using the RigidScale keyword. The quantity
is specified using the RigidScale keyword. The quantity  in Eqs. eq:rigidvdw and eq:h_func sets radius of the atomic sphere for atom
in Eqs. eq:rigidvdw and eq:h_func sets radius of the atomic sphere for atom  . By default,
. By default,  but this can be controlled as described below.
but this can be controlled as described below.
RigidScale
Sets the length scale on which the error function employed in the rigid vdW cavity construction interpolates the dielectric value from vacuum to solvent.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
0.265 Å
OPTIONS:

Specifies the desired value (in Å); see Eq. eq:h_func.
RECOMMENDATION:
Use the default value, which was tuned in Ref. Fisicaro:2016 so that errors in small-molecule solvation energies were
kcal/mol.
VDWType
Specifies details for the rigid vdW cavity construction.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
Scaled
OPTIONS:
Unscaled

Scaled

Shifted

RECOMMENDATION:
None. The values of
and
are set with the VDWScale and VDWShift keywords.
VDWScale
Sets the empirical scale factor applied to the atomic van der Waals radius.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
1.2
OPTIONS:

Specifies the desired dimensionless scaling factor for the atomic vdW radii.
RECOMMENDATION:
Use the default value.
VDWShift
Adjusts the center of the spherically-symmetric error functions when constructing the rigid vdW cavity.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
0.0 Ångstroms
OPTIONS:

Specifies the desired shift (in Å).
RECOMMENDATION:
None. If VDWType is set to Shifted, the vdW scale factor is set to 1.0 by default. This can be adjusted using the VDWScale keyword.
Setting the SoluteCavity keyword to Spherical requests the construction of a spherical cavity around the solute, and the dielectric is smoothly interpolated from vacuum to solvent using a hyperbolic tangent function:[Coons et al.(2016)Coons, You, and Herbert]
![\begin{equation} \label{eq:hyperbolic} \varepsilon (r) = \frac{1}{2}\Bigl \{ (\varepsilon _\ensuremath{\mathrm{}}{solvent} + 1) + (\varepsilon _\ensuremath{\mathrm{}}{solvent} - 1) \mbox{tanh}\bigl [\alpha (r - r_\ensuremath{\mathrm{}}{mid})\bigr ] \Bigr \} \; . \end{equation}](images/img-2151.png) |
(12.41) |
Here,  is the distance where the dielectric assumes the value
is the distance where the dielectric assumes the value  . The value of
. The value of  is taken to be the sum of the sphere radius,
is taken to be the sum of the sphere radius, 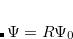 , and half of the interpolation length,
, and half of the interpolation length, 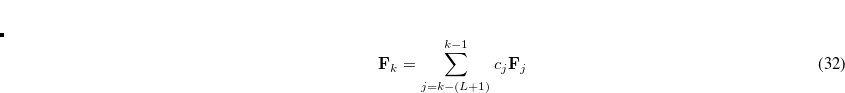 :
:  . The sphere radius and interpolation length are controlled with the SphereRadius and InterpolLength keywords described below. The parameter
. The sphere radius and interpolation length are controlled with the SphereRadius and InterpolLength keywords described below. The parameter 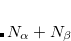 controls the sharpness of the switching process, with
controls the sharpness of the switching process, with  by default.
by default.
SphereRadius
Sets the radius of the spherical solute cavity.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
No default.
OPTIONS:
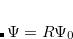
Desired spherical cavity radius (in Å).
RECOMMENDATION:
None. See the Supporting Information of Ref. Coons:2016 for more information.
InterpolLength
Sets the length scale on which the dielectric is smoothly interpolated from vacuum to solvent.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
No default.
OPTIONS:
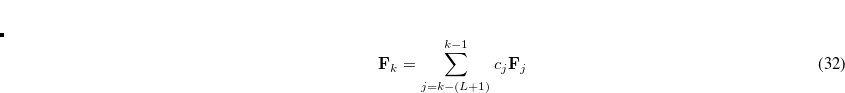
Desired interpolation length (in Å).
RECOMMENDATION:
None.
InterpolScale
For a given interpolation length (
), InterpolScale (
) sets the sharpness of the dielectric transition from vacuum to solvent.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
=

OPTIONS:
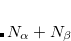
Desired interpolation scale factor (in Å
).
RECOMMENDATION:
Use the default unless a broader (smaller
) or narrower (larger
) transition region is desired.
Interface
Perform a solvation calculation at a solvent/vacuum interface.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
False
OPTIONS:
True
Modify the dielectric function to simulate an interface between solvent and vacuum.
False
Perform a solvation calculation in bulk solvent.
RECOMMENDATION:
The user will also need to specify the length scale on which the dielectric is smoothly interpolated from the bulk solvent value to vacuum, and the location of the Gibbs dividing surface (see below).
By setting Interface = True, the dielectric function on the Cartesian grid is further modified to mimic a solvent/vacuum interface. First, the solute cavity is constructed as specified by the SoluteCavity keyword as discussed above. Then, the dielectric function is smoothly interpolated in the  direction across the Gibbs dividing surface (
direction across the Gibbs dividing surface ( ) using the following hyperbolic tangent switching function:[Coons et al.(2016)Coons, You, and Herbert, Coons and Herbert(2018)]
) using the following hyperbolic tangent switching function:[Coons et al.(2016)Coons, You, and Herbert, Coons and Herbert(2018)]
![\begin{equation} \label{eq:hyperbolic2} \varepsilon (z) = \frac{1}{2}\Bigl \{ (\varepsilon _{\rm solvent} + 1) + (1 - \varepsilon _{\rm solvent}) \mbox{tanh}\bigl [\beta (z - z^{}_\ensuremath{\mathrm{}}{GDS})\bigr ] \Bigr \} \; . \end{equation}](images/img-2158.png) |
(12.42) |
This interpolates the dielectric function over the interface length  , centered at the Gibbs dividing surface,
, centered at the Gibbs dividing surface,  . Both of these values are controlled by the keywords InterfaceLength and GibbsDS, respectively. Similar to the parameter
. Both of these values are controlled by the keywords InterfaceLength and GibbsDS, respectively. Similar to the parameter 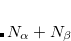 used in the spherical cavity construction, the parameter
used in the spherical cavity construction, the parameter  controls the sharpness of the interpolation across the Gibbs dividing surface.
controls the sharpness of the interpolation across the Gibbs dividing surface.
InterfaceLength
Sets the length scale over which the dielectric function is smoothly transitioned from bulk solvent to vacuum in the
direction
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
None
OPTIONS:

Desired interface length (in Å).
RECOMMENDATION:
This sets the value
in Eq. eq:hyperbolic2. See the Supporting Information of Ref. Coons:2016 for a full description of the solvent/vacuum interface construction.
GibbsDS
Sets the location of the Gibbs dividing surface, in the
direction.
INPUT SECTION: $peqs
TYPE:
FLOAT
DEFAULT:
None
OPTIONS:

Desired location of the Gibbs dividing surface (in Å).
RECOMMENDATION:
Consult the literature. One such way to determine this value is to compute a density profile of the solvent as a function of
and set this location to be where the solvent density has decreased to 50% of the bulk value. Usually
.
NonequilJob
Obtain the nonequilibrium free energy of solvation for a vertical ionization process.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
False
OPTIONS:
True
Compute the nonequilibrium free energy for a vertical ionization process.
False
Compute the equilibrium solvation free energy.
RECOMMENDATION:
None.
NonequilPartition
Specifies the manner in which the solvent response is partitioned into fast and slow components.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
Marcus
OPTIONS:
Marcus
Employ the Marcus partitioning scheme.
Pekar
Employ the Pekar partitioning scheme.
RECOMMENDATION:
Use the default. Although the fast and slow solvation responses are different between the two approaches, the total solvation free energy is the same,You:2015 but the Pekar scheme is computationally more expensive than the Marcus scheme.
NonequilState
Specifies the state of interest for a nonequilibrium vertical ionization.
INPUT SECTION: $peqs
TYPE:
STRING
DEFAULT:
Reference
OPTIONS:
Reference
The reference (initial) state, from which an electron will be removed.
Ionized
The final (ionized) state.
RECOMMENDATION:
None. Both values will be needed in a compound input job, in order to compute the nonequilibrium response to vertical ionization; see Example 12.2.10.4.
12.2.10.4 Examples
The following example computes the solvation free energy of a water molecule immersed in water. The Cartesian grid is cubic with a side length of 15.0 Å and 73 grid points in each direction. A rigid vdW cavity is used based on scaled vdW radii for the atomic spheres. The dielectric is not set, so takes the default value of 78.39.
Example 12.296 Free energy of solvation of water in water.
$rem
SCF_CONVERGENCE 5
THRESH 14
EXCHANGE wB97X-V
BASIS 6-31+G*
SOLVE_PEQ TRUE
PEQ_SWITCH 0
$end
$molecule
0 1
O 0.053004 -0.020947 -0.034784
H 0.003424 0.185855 0.910594
H -0.844842 0.146674 -0.358413
$end
$peqs
SOLUTECAVITY RIGIDVDW
$end
$peqs_grid
DimX 73 -7.50 7.50
DimY 73 -7.50 7.50
DimZ 73 -7.50 7.50
$end
The next example illustrates calculation of the solvation free energy of a water molecule at a water/vacuum interface, with the Gibbs dividing surface placed at  Å. The length of the interface is set to
Å. The length of the interface is set to  Å and the dielectric is interpolated from bulk solvent to vacuum in the positive
Å and the dielectric is interpolated from bulk solvent to vacuum in the positive  direction across the Gibbs dividing surface. The Cartesian grid, solute cavity, and solvent dielectric are the same as in the previous example.
direction across the Gibbs dividing surface. The Cartesian grid, solute cavity, and solvent dielectric are the same as in the previous example.
Example 12.297 Free energy of solvation of water at a water/vacuum interface.
$rem
SCF_CONVERGENCE 5
THRESH 14
EXCHANGE wB97X-V
BASIS 6-31+G*
SOLVE_PEQ TRUE
PEQ_SWITCH 0
$end
$molecule
0 1
O 0.053004 -0.020947 -0.034784
H 0.003424 0.185855 0.910594
H -0.844842 0.146674 -0.358413
$end
$peqs
SOLUTECAVITY RIGIDVDW
INTERFACE TRUE
INTERFACELENGTH 2.75
GIBBSDS 0.50
INTERFACEDIRECTION POSITIVE
$end
$peqs_grid
DimX 73 -7.50 7.50
DimY 73 -7.50 7.50
DimZ 73 -7.50 7.50
$end
The final example illustrates a nonequilibrium (NonEquilJob = True) solvation calculation for the vertical ionization of  in bulk water. This is a compound job that first calculates the equilibrium solvation free energy of the anionic state (NonEquilState = Reference), then computes the nonequilibrium energy correction for the ionized state (NonEquilState = Ionized). The two jobs are separated by “@@@”. The Cartesian grid and solvent dielectric are the same as the previous examples, but the solute cavity is chosen to be spherical with a radius of 2.0 Å. The Marcus scheme (NonEquilPartition = Marcus) is used to partition the solvent response into fast and slow components. Since this is the default method, the NonEquilPartition keyword is omitted.
in bulk water. This is a compound job that first calculates the equilibrium solvation free energy of the anionic state (NonEquilState = Reference), then computes the nonequilibrium energy correction for the ionized state (NonEquilState = Ionized). The two jobs are separated by “@@@”. The Cartesian grid and solvent dielectric are the same as the previous examples, but the solute cavity is chosen to be spherical with a radius of 2.0 Å. The Marcus scheme (NonEquilPartition = Marcus) is used to partition the solvent response into fast and slow components. Since this is the default method, the NonEquilPartition keyword is omitted.
Example 12.298 Nonequilibrium free energy of solvation for the vertical ionization of 
$rem
SCF_CONVERGENCE 5
THRESH 14
EXCHANGE HF
BASIS 6-31++G*
SOLVE_PEQ TRUE
PEQ_SWITCH 0
$end
$molecule
-1 2
O 0.053004 -0.020947 -0.034784
H 0.003424 0.185855 0.910594
H -0.844842 0.146674 -0.358413
$end
$peqs
SOLUTECAVITY SPHERICAL
SPHERERADIUS 2.00
NONEQUILJOB TRUE
NONEQUILSTATE REFERENCE
$end
$peqs_grid
DimX 73 -7.50 7.50
DimY 73 -7.50 7.50
DimZ 73 -7.50 7.50
$end
@@@
$rem
SCF_CONVERGENCE 5
THRESH 14
EXCHANGE HF
BASIS 6-31++G*
SOLVE_PEQ TRUE
PEQ_SWITCH 0
$end
$molecule
0 1
O 0.053004 -0.020947 -0.034784
H 0.003424 0.185855 0.910594
H -0.844842 0.146674 -0.358413
$end
$peqs
SOLUTECAVITY SPHERICAL
SPHERERADIUS 2.00
NONEQUILJOB TRUE
NONEQUILSTATE IONIZED
$end
$peqs_grid
DimX 73 -7.50 7.50
DimY 73 -7.50 7.50
DimZ 73 -7.50 7.50
$end









































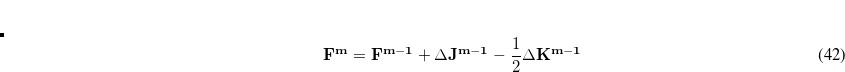 -ethylbenzoate
-ethylbenzoate -1,2-dimethylcyclohexane
-1,2-dimethylcyclohexane  -chlorotoluene
-chlorotoluene  -1,2-dichloroethene
-1,2-dichloroethene -xylene
-xylene -butanol
-butanol -butanol
-butanol -decalin
-decalin -1,2-dichloroethene
-1,2-dichloroethene


 (default is 0.0), where
(default is 0.0), where  is the macroscopic surface tension at air/solvent
is the macroscopic surface tension at air/solvent  is 1 cal mol
is 1 cal mol (1 dyne/cm = 1.43932 cal mol
(1 dyne/cm = 1.43932 cal mol : the fraction of non-hydrogenic solvent atoms that are
: the fraction of non-hydrogenic solvent atoms that are 


