11.2 Wave Function Analysis
Q-Chem performs a number of standard wave function analyses by default. Switching the $rem variable WAVEFUNCTION_ANALYSIS to FALSE will prevent the calculation of all wave function analysis features (described in this section). Alternatively, each wave function analysis feature may be controlled by its $rem variable. (The NBO program, which is interfaced with Q-Chem, is capable of performing more sophisticated analyses. See Section 11.3 of this manual, along with the NBO manual, for more details.
WAVEFUNCTION_ANALYSIS
Controls the running of the default wave function analysis tasks.
TYPE:
LOGICAL
DEFAULT:
TRUE
OPTIONS:
TRUE
Perform default wave function analysis.
FALSE
Do not perform default wave function analysis.
RECOMMENDATION:
None
Note: WAVEFUNCTION_ANALYSIS has no effect on NBO, solvent models or vibrational analyses.
11.2.1 Population Analysis
The one-electron charge density, usually written as
 |
(11.1) |
represents the probability of finding an electron at the point 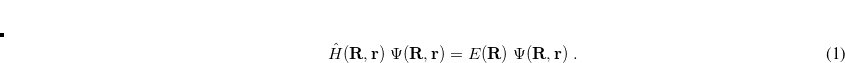 , but implies little regarding the number of electrons associated with a given nucleus in a molecule. However, since the number of electrons
, but implies little regarding the number of electrons associated with a given nucleus in a molecule. However, since the number of electrons  is related to the occupied orbitals
is related to the occupied orbitals  by
by
 |
(11.2) |
We can substitute the atomic orbital (AO) basis expansion of  into Eq. (11.2) to obtain
into Eq. (11.2) to obtain
 |
(11.3) |
where we interpret  as the number of electrons associated with
as the number of electrons associated with  . If the basis functions are atom-centered, the number of electrons associated with a given atom can be obtained by summing over all the basis functions. This leads to the Mulliken formula for the net charge of the atom
. If the basis functions are atom-centered, the number of electrons associated with a given atom can be obtained by summing over all the basis functions. This leads to the Mulliken formula for the net charge of the atom  :
:
 |
(11.4) |
where  is the atom’s nuclear charge. This is called a Mulliken population analysis.[Szabo and Ostlund(1996)] Q-Chem performs a Mulliken population analysis by default.
is the atom’s nuclear charge. This is called a Mulliken population analysis.[Szabo and Ostlund(1996)] Q-Chem performs a Mulliken population analysis by default.
POP_MULLIKEN
Controls running of Mulliken population analysis.
TYPE:
LOGICAL/INTEGER
DEFAULT:
TRUE (or 1)
OPTIONS:
FALSE (or 0)
Do not calculate Mulliken populations.
TRUE (or 1)
Calculate Mulliken populations.
2
Also calculate shell populations for each occupied orbital.

Calculate Mulliken charges for both the ground state and any CIS,
RPA, or TDDFT excited states.
RECOMMENDATION:
Leave as TRUE, unless excited-state charges are desired. Mulliken analysis is a trivial additional calculation, for ground or excited states.
LOWDIN_POPULATION
Run Löwdin population analysis.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Do not calculate Löwdin populations.
TRUE
Run Löwdin population analysis.
RECOMMENDATION:
None
Although conceptually simple, Mulliken population analyses suffer from a heavy dependence on the basis set used, as well as the possibility of producing unphysical negative numbers of electrons. An alternative is that of Löwdin population analysis,[Löwdin(1950)] which uses the Löwdin symmetrically orthogonalized basis set (which is still atom-tagged) to assign the electron density. This shows a reduced basis set dependence, but maintains the same essential features.
While Mulliken and Löwdin population analyses are commonly employed, and can be used to produce information about changes in electron density and also localized spin polarizations, they should not be interpreted as oxidation states of the atoms in the system. For such information we would recommend a bonding analysis technique (LOBA or NBO).
A more stable alternative to Mulliken or Löwdin charges are the so-called “ChElPG” charges (“Charges from the Electrostatic Potential on a Grid”).[Breneman and Wiberg(1990)] These are the atom-centered charges that provide the best fit to the molecular electrostatic potential, evaluated on a real-space grid outside of the van der Waals region and subject to the constraint that the sum of the ChElPG charges must equal the molecular charge. Q-Chem’s implementation of the ChElPG algorithm differs slightly from the one originally algorithm described by Breneman and Wiberg,[Breneman and Wiberg(1990)] in that Q-Chem weights the grid points with a smoothing function to ensure that the ChElPG charges vary continuously as the nuclei are displaced.[Herbert et al.(2012)Herbert, Jacobson, Lao, and Rohrdanz] (For any particular geometry, however, numerical values of the charges are quite similar to those obtained using the original algorithm.) Note, however, that the Breneman-Wiberg approach uses a Cartesian grid and becomes expensive for large systems. (It is especially expensive when ChElPG charges are used in QM/MM-Ewald calculations.[Holden et al.(2013)Holden, Richard, and Herbert]) For that reason, an alternative procedure based on atom-centered Lebedev grids is also available,[Holden et al.(2013)Holden, Richard, and Herbert] which provides very similar charges using far fewer grid points. In order to use the Lebedev grid implementation the $rem variables CHELPG_H and CHELPG_HA must be set, which specify the number of Lebedev grid points for the hydrogen atoms and the heavy atoms, respectively.
CHELPG
Controls the calculation of CHELPG charges.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Do not calculate ChElPG charges.
TRUE
Compute ChElPG charges.
RECOMMENDATION:
Set to TRUE if desired. For large molecules, there is some overhead associated with computing ChElPG charges, especially if the number of grid points is large.
CHELPG_HEAD
Sets the “head space”[Breneman and Wiberg(1990)] (radial extent) of the ChElPG grid.
TYPE:
INTEGER
DEFAULT:
30
OPTIONS:

Corresponding to a head space of
, in Å.
RECOMMENDATION:
Use the default, which is the value recommended by Breneman and Wiberg.[Breneman and Wiberg(1990)]
CHELPG_DX
Sets the rectangular grid spacing for the traditional Cartesian ChElPG grid or the spacing between concentric Lebedev shells (when the variables CHELPG_HA and CHELPG_H are specified as well).
TYPE:
INTEGER
DEFAULT:
6
OPTIONS:

Corresponding to a grid space of
, in Å.
RECOMMENDATION:
Use the default, which corresponds to the “dense grid” of Breneman and Wiberg,[Breneman and Wiberg(1990)], unless the cost is prohibitive, in which case a larger value can be selected. Note that this default value is set with the Cartesian grid in mind and not the Lebedev grid. In the Lebedev case, a larger value can typically be used.
CHELPG_H
Sets the Lebedev grid to use for hydrogen atoms.
TYPE:
INTEGER
DEFAULT:
NONE
OPTIONS:

Corresponding to a number of points in a Lebedev grid.
RECOMMENDATION:
CHELPG_H must always be less than or equal to CHELPG_HA. If it is greater, it will automatically be set to the value of CHELPG_HA.
CHELPG_HA
Sets the Lebedev grid to use for non-hydrogen atoms.
TYPE:
INTEGER
DEFAULT:
NONE
OPTIONS:

Corresponding to a number of points in a Lebedev grid (see Section 5.5.1.
RECOMMENDATION:
None.
Finally, Hirshfeld population analysis[Hirshfeld(1977)] provides yet another definition of atomic charges in molecules via a Stockholder prescription. The charge on atom  ,
, 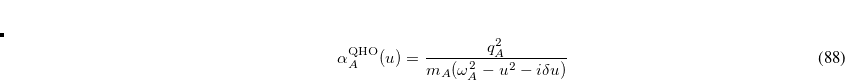 , is defined by
, is defined by
 |
(11.5) |
where  is the nuclear charge of
is the nuclear charge of  ,
,  is the isolated ground-state atomic density of atom
is the isolated ground-state atomic density of atom  , and
, and 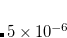 is the molecular density. The sum goes over all atoms in the molecule. Thus computing Hirschfeld charges requires a self-consistent calculation of the isolated atomic densities (the promolecule) as well as the total molecule. Following SCF completion, the Hirschfeld analysis proceeds by running another SCF calculation to obtain the atomic densities. Next numerical quadrature is used to evaluate the integral in Eq. (11.5). Neutral ground-state atoms are used, and the choice of appropriate reference for a charged molecule is ambiguous (such jobs will crash). As numerical integration (with default quadrature grid) is used, charges may not sum precisely to zero. A larger XC_GRID may be used to improve the accuracy of the integration.
is the molecular density. The sum goes over all atoms in the molecule. Thus computing Hirschfeld charges requires a self-consistent calculation of the isolated atomic densities (the promolecule) as well as the total molecule. Following SCF completion, the Hirschfeld analysis proceeds by running another SCF calculation to obtain the atomic densities. Next numerical quadrature is used to evaluate the integral in Eq. (11.5). Neutral ground-state atoms are used, and the choice of appropriate reference for a charged molecule is ambiguous (such jobs will crash). As numerical integration (with default quadrature grid) is used, charges may not sum precisely to zero. A larger XC_GRID may be used to improve the accuracy of the integration.
The charges (and corresponding molecular dipole moments) obtained using Hirschfeld charges are typically underestimated as compared to other charge schemes or experimental data. To correct this, Marenich et al. introduced “Charge Model 5” (CM5),[Marenich et al.(2012)Marenich, Jerome, Cramer, and Truhlar] which employs a single set of parameters to map the Hirschfeld charges onto a more reasonable representation of the electrostatic potential. CM5 charges generally lead to more accurate dipole moments as compared to the original Hirschfeld charges, at negligible additional cost. CM5 is available for molecules composed of elements H–Ca, Zn, Ge–Br, and I.
The use of neutral ground-state atoms to define the promolecular density in Hirshfeld scheme has no strict theoretical basis and there is no unique way to construct the promolecular densities. For example, Li F
F , Li
, Li F
F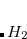 , or Li
, or Li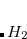 F
F could each be used to construct the promolecular densities for LiF. Furthermore, the choice of appropriate reference for a charged molecule is ambiguous, and for this reason Hirshfeld analysis is disable in Q-Chem for any molecule with a net charge. A solution for charged molecules is to use the iterative “Hirshfeld-I” partitioning scheme proposed by Bultinck et al.,[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Vanpoucke et al.(2013)Vanpoucke, Bultinck, and Van Driessche] in which the reference state is not predefined but rather determined self-consistently, thus eliminating the arbitrariness. The final self-consistent reference state for Hirshfeld-I partitioning usually consists of non-integer atomic populations.
could each be used to construct the promolecular densities for LiF. Furthermore, the choice of appropriate reference for a charged molecule is ambiguous, and for this reason Hirshfeld analysis is disable in Q-Chem for any molecule with a net charge. A solution for charged molecules is to use the iterative “Hirshfeld-I” partitioning scheme proposed by Bultinck et al.,[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Vanpoucke et al.(2013)Vanpoucke, Bultinck, and Van Driessche] in which the reference state is not predefined but rather determined self-consistently, thus eliminating the arbitrariness. The final self-consistent reference state for Hirshfeld-I partitioning usually consists of non-integer atomic populations.
In the first iteration, the Hirshfeld-I method uses neutral atomic densities (as in the original Hirshfeld scheme),  with electronic population
with electronic population  . This affords charges
. This affords charges
 |
(11.6) |
on the first iteration. The new electronic population (number of electrons) for atom  is
is  , and is derived from the promolecular populations
, and is derived from the promolecular populations  . One then computes new isolated atomic densities with
. One then computes new isolated atomic densities with  and uses them to construct the promolecular densities in the next iteration. In general, the new weighting function for atom
and uses them to construct the promolecular densities in the next iteration. In general, the new weighting function for atom  in the
in the 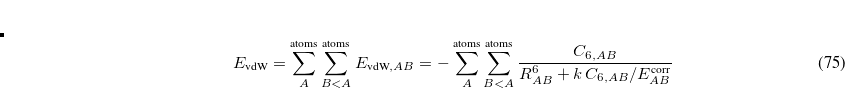 th iteration is
th iteration is
 |
(11.7) |
The atomic densities  with corresponding fractional electron numbers
with corresponding fractional electron numbers  are obtained by linear interpolation between
are obtained by linear interpolation between  and
and  of the same atom:[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Elking et al.(2012)Elking, Perera, and Pedersen]
of the same atom:[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Elking et al.(2012)Elking, Perera, and Pedersen]
 |
(11.8) |
where  and
and  denote the integers that bracket
denote the integers that bracket  The two atomic densities on the right side of Eq. eq:interpolate are obtained from densities
The two atomic densities on the right side of Eq. eq:interpolate are obtained from densities  that are computed in advance. (That is, the method uses the neutral atomic density along with the densities for the singly- and doubly-charged cations and anions of the element in equation.) The Hirshfeld-I iterations are converged once the atomic populations change insignificantly between iterations, say
that are computed in advance. (That is, the method uses the neutral atomic density along with the densities for the singly- and doubly-charged cations and anions of the element in equation.) The Hirshfeld-I iterations are converged once the atomic populations change insignificantly between iterations, say  .[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Steinmann and Corminbeoeuf(2010)]
.[Bultinck et al.(2007)Bultinck, Van Alsenoy, Ayers, and Carbó-Dorca, Steinmann and Corminbeoeuf(2010)]
The iterative Hirshfeld scheme generally affords more reasonable charges as compared to the original Hirshfeld scheme. In LiF, for example, the original Hirshfeld scheme predicts atomic charges of  0.57 while the iterative scheme increases these charges to
0.57 while the iterative scheme increases these charges to  0.93. The integral in Eq. eq:hirshc is evaluated by numerical quadrature, and the cost of each iteration of Hirshfeld-I is equal to the cost of computing the original Hirshfeld charges. Within Q-Chem, Hirshfeld-I charges are available for molecules containing only H, Li, C, N, O, F, S, and Cl. The $rem variable SYM_IGNORE must be set to TRUE for Hirshfeld-I analysis.
0.93. The integral in Eq. eq:hirshc is evaluated by numerical quadrature, and the cost of each iteration of Hirshfeld-I is equal to the cost of computing the original Hirshfeld charges. Within Q-Chem, Hirshfeld-I charges are available for molecules containing only H, Li, C, N, O, F, S, and Cl. The $rem variable SYM_IGNORE must be set to TRUE for Hirshfeld-I analysis.
HIRSHFELD
Controls running of Hirshfeld population analysis.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate Hirshfeld populations.
FALSE
Do not calculate Hirshfeld populations.
RECOMMENDATION:
None
HIRSHFELD_READ
Switch to force reading in of isolated atomic densities.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Read in isolated atomic densities from previous Hirshfeld calculation from disk.
FALSE
Generate new isolated atomic densities.
RECOMMENDATION:
Use the default unless system is large. Note, atoms should be in the same order with same basis set used as in the previous Hirshfeld calculation (although coordinates can change). The previous calculation should be run with the -save switch.
HIRSHFELD_SPHAVG
Controls whether atomic densities should be spherically averaged in pro-molecule.
TYPE:
LOGICAL
DEFAULT:
TRUE
OPTIONS:
TRUE
Spherically average atomic densities.
FALSE
Do not spherically average.
RECOMMENDATION:
Use the default.
CM5
Controls running of CM5 population analysis.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate CM5 populations.
FALSE
Do not calculate CM5 populations.
RECOMMENDATION:
None
HIRSHITER
Controls running of iterative Hirshfeld population analysis.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate iterative Hirshfeld populations.
FALSE
Do not calculate iterative Hirshfeld populations.
RECOMMENDATION:
None
HIRSHITER_THRESH
Controls the convergence criterion of iterative Hirshfeld population analysis.
TYPE:
INTEGER
DEFAULT:
5
OPTIONS:

Corresponding to the convergence criterion of
, in
.
RECOMMENDATION:
Use the default, which is the value recommended in Ref. Bultinck:2007
Example 11.241 Iterative Hirshfeld population analysis for 
$molecule
-1 1
O 1.197566 -0.108087 0.000000
H 1.415397 0.827014 0.000000
H 0.134830 -0.084378 0.000000
F -1.236389 0.012239 0.000000
$end
$rem
SYM_IGNORE true
METHOD B3LYP
BASIS 6-31G*
HIRSHITER true
$end
11.2.2 Multipole Moments
This section discusses how to compute arbitrary electrostatic multipole moments for an entire molecule, including both ground- and excited-state electron densities. Occasionally, however, it is useful to decompose the electronic part of the multipole moments into contributions from individual MOs. This decomposition is especially useful for systems containing unpaired electrons,[Williams and Herbert(2008)] where the first-order moments  ,
,  , and
, and  characterize the centroid (mean position) of the half-filled MO, and the second-order moments determine its radius of gyration,
characterize the centroid (mean position) of the half-filled MO, and the second-order moments determine its radius of gyration,  , which characterizes the size of the MO. Upon setting PRINT_RADII_GYRE = TRUE, Q-Chem will print out centroids and radii of gyration for each occupied MO and for the overall electron density. If CIS or TDDFT excited states are requested, then this keyword will also print out the centroids and radii of gyration for each excited-state electron density.
, which characterizes the size of the MO. Upon setting PRINT_RADII_GYRE = TRUE, Q-Chem will print out centroids and radii of gyration for each occupied MO and for the overall electron density. If CIS or TDDFT excited states are requested, then this keyword will also print out the centroids and radii of gyration for each excited-state electron density.
PRINT_RADII_GYRE
Controls printing of MO centroids and radii of gyration.
TYPE:
LOGICAL/INTEGER
DEFAULT:
FALSE
OPTIONS:
TRUE (or 1)
Print the centroid and radius of gyration for each occupied MO and each density.
2
Print centroids and radii of gyration for the virtual MOs as well.
FALSE (or 0)
Do not calculate these quantities.
RECOMMENDATION:
None
Q-Chem can compute Cartesian multipole moments of the charge density to arbitrary order, both for the ground state and for excited states calculated using the CIS or TDDFT methods.
MULTIPOLE_ORDER
Determines highest order of multipole moments to print if wave function analysis requested.
TYPE:
INTEGER
DEFAULT:
4
OPTIONS:

Calculate moments to
th order.
RECOMMENDATION:
Use the default unless higher multipoles are required.
CIS_MOMENTS
Controls calculation of excited-state (CIS or TDDFT) multipole moments
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Do not calculate excited-state moments.
TRUE
Calculate moments for each excited state.
RECOMMENDATION:
Set to TRUE if excited-state moments are desired. (This is a trivial additional calculation.) The MULTIPOLE_ORDER controls how many multipole moments are printed.
11.2.3 Symmetry Decomposition
Q-Chem’s default is to write the SCF wave function molecular orbital symmetries and energies to the output file. If requested, a symmetry decomposition of the kinetic and nuclear attraction energies can also be calculated.
SYMMETRY_DECOMPOSITION
Determines symmetry decompositions to calculate.
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
0
No symmetry decomposition.
1
Calculate MO eigenvalues and symmetry (if available).
2
Perform symmetry decomposition of kinetic energy and nuclear attraction
matrices.
RECOMMENDATION:
None
11.2.4 Localized Orbital Bonding Analysis
Localized orbital bonding analysis[Thom et al.(2009)Thom, Sundstrom, and Head-Gordon] (LOBA) is a technique developed by Dr. Alex Thom and Eric Sundstrom at Berkeley with Prof. Martin Head-Gordon. Inspired by the work of Rhee and Head-Gordon,[Rhee and Head-Gordon(2008)] it makes use of the fact that the post-SCF localized occupied orbitals of a system provide a large amount of information about the bonding in the system.
While the canonical molecular orbitals can provide information about local reactivity and ionization energies, their delocalized nature makes them rather uninformative when looking at the bonding in larger molecules. Localized orbitals in contrast provide a convenient way to visualize and account for electrons. Transformations of the orbitals within the occupied subspace do not alter the resultant density; if a density can be represented as orbitals localized on individual atoms, then those orbitals can be regarded as non-bonding. If a maximally localized set of orbitals still requires some to be delocalized between atoms, these can be regarded as bonding electrons. A simple example is that of He versus H
versus H . In the former, the delocalized
. In the former, the delocalized  and
and  canonical orbitals may be transformed into 1s orbitals on each He atom, and there is no bond between them. This is not possible for the H
canonical orbitals may be transformed into 1s orbitals on each He atom, and there is no bond between them. This is not possible for the H molecule, and so we can regard there being a bond between the atoms. In cases of multiple bonding, multiple delocalized orbitals are required.
molecule, and so we can regard there being a bond between the atoms. In cases of multiple bonding, multiple delocalized orbitals are required.
While there are no absolute definitions of bonding and oxidation state, it has been shown that the localized orbitals match the chemically intuitive notions of core, non-bonded, single- and double-bonded electrons, etc.. By combining these localized orbitals with population analyses, LOBA allows the nature of the bonding within a molecule to be quickly determined.
In addition, it has been found that by counting localized electrons, the oxidation states of transition metals can be easily found. Owing to polarization caused by ligands, an upper threshold is applied, populations above which are regarded as “localized” on an atom, which has been calibrated to a range of transition metals, recovering standard oxidation states ranging from 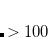 II to VII.
II to VII.
LOBA
Specifies the methods to use for LOBA
TYPE:
INTEGER
DEFAULT:
00
OPTIONS:


specifies the localization method
0 Perform Boys localization.
1 Perform PM localization.
2 Perform ER localization.

specifies the population analysis method
0 Do not perform LOBA. This is the default.
1 Use Mulliken population analysis.
2 Use Löwdin population analysis.
RECOMMENDATION:
Boys Localization is the fastest. ER will require an auxiliary basis set.
LOBA 12 provides a reasonable speed/accuracy compromise.
LOBA_THRESH
Specifies the thresholds to use for LOBA
TYPE:
INTEGER
DEFAULT:
6015
OPTIONS:

specifies the threshold to use for localization
specifies the threshold to use for occupation
Both are given as percentages.
RECOMMENDATION:
Decrease
to see the smaller contributions to orbitals. Values of
between 40 and 75 have been shown to given meaningful results.
On a technical note, LOBA can function of both restricted and unrestricted SCF calculations. The figures printed in the bonding analysis count the number of electrons on each atom from that orbital (i.e., up to 1 for unrestricted or singly occupied restricted orbitals, and up to 2 for double occupied restricted.)
11.2.5 Basic Excited-State Analysis of CIS and TDDFT Wave Functions
For CIS, TDHF, and TDDFT excited-state calculations, we have already mentioned that Mulliken population analysis of the excited-state electron densities may be requested by setting POP_MULLIKEN =  , and multipole moments of the excited-state densities will be generated if CIS_MOMENTS = TRUE. Another useful decomposition for excited states is to separate the excitation into “particle” and “hole” components, which can then be analyzed separately.[Richard and Herbert(2011)] To do this, we define a density matrix for the excited electron,
, and multipole moments of the excited-state densities will be generated if CIS_MOMENTS = TRUE. Another useful decomposition for excited states is to separate the excitation into “particle” and “hole” components, which can then be analyzed separately.[Richard and Herbert(2011)] To do this, we define a density matrix for the excited electron,
 |
(11.9) |
and a density matrix for the hole that is left behind in the occupied space:
 |
(11.10) |
The quantities  and
and  are the transition density matrices, i.e., the components of the TDDFT eigenvector.[Dreuw and Head-Gordon(2005)] The indices
are the transition density matrices, i.e., the components of the TDDFT eigenvector.[Dreuw and Head-Gordon(2005)] The indices  and
and 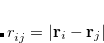 denote MOs that occupied in the ground state, whereas
denote MOs that occupied in the ground state, whereas  and
and  index virtual MOs. Note also that
index virtual MOs. Note also that  , the difference between the ground- and excited-state density matrices.
, the difference between the ground- and excited-state density matrices.
Upon transforming  and
and  into the AO basis, one can write
into the AO basis, one can write
 |
(11.11) |
where  is the total charge that is transferred from the occupied space to the virtual space. For a CIS calculation, or for TDDFT within the Tamm-Dancoff approximation,[Hirata et al.(2000)Hirata, Nooijen, and Bartlett]
is the total charge that is transferred from the occupied space to the virtual space. For a CIS calculation, or for TDDFT within the Tamm-Dancoff approximation,[Hirata et al.(2000)Hirata, Nooijen, and Bartlett]  . For full TDDFT calculations,
. For full TDDFT calculations,  may be slightly different than
may be slightly different than  .
.
Comparison of Eq. () to Eq. (11.3) suggests that the quantities  and
and  are amenable to population analyses of precisely the same sort used to analyze the ground-state density matrix. In particular,
are amenable to population analyses of precisely the same sort used to analyze the ground-state density matrix. In particular,  represents the
represents the 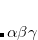 th AO’s contribution to the excited electron, while
th AO’s contribution to the excited electron, while  is a contribution to the hole. The sum of these quantities,
is a contribution to the hole. The sum of these quantities,
 |
(11.12) |
represents the contribution to  arising from the
arising from the 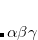 th AO. For the particle/hole density matrices, both Mulliken and Löwdin population analyses available, and are requested by setting CIS_MULLIKEN = TRUE.
th AO. For the particle/hole density matrices, both Mulliken and Löwdin population analyses available, and are requested by setting CIS_MULLIKEN = TRUE.
CIS_MULLIKEN
Controls Mulliken and Löwdin population analyses for excited-state particle and hole density matrices.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Do not perform particle/hole population analysis.
TRUE
Perform both Mulliken and Löwdin analysis of the particle and hole
density matrices for each excited state.
RECOMMENDATION:
Set to TRUE if desired. This represents a trivial additional calculation.
Although the excited-state analysis features described in this section require very little computational effort, they are turned off by default, because they can generate a large amount of output, especially if a large number of excited states are requested. They can be turned on individually, or collectively by setting CIS_AMPL_ANAL = TRUE. This collective option also requests the calculation of natural transition orbitals (NTOs), which were introduced in Section 7.12.2. (NTOs can also be requested without excited-state population analysis. Some practical aspects of calculating and visualizing NTOs are discussed below, in Section 11.5.2.)
CIS_AMPL_ANAL
Perform additional analysis of CIS and TDDFT excitation amplitudes, including generation of natural transition orbitals, excited-state multipole moments, and Mulliken analysis of the excited state densities and particle/hole density matrices.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Perform additional amplitude analysis.
FALSE
Do not perform additional analysis.
RECOMMENDATION:
None
11.2.6 General Excited-State Analysis
Q-Chem features a new module for extended excited-state analysis, which is interfaced to the ADC, CC/EOM-CC, CIS, and TDDFT methods.[Plasser and Lischka(2012), Plasser et al.(2014b)Plasser, Wormit, and Dreuw, Plasser et al.(2014a)Plasser, Bäppler, Wormit, and Dreuw, Bäppler et al.(2014)Bäppler, Plasser, Wormit, and Dreuw, Plasser et al.(2015)Plasser, Thomitzni, Bäppler, Wenzel, Rehn, Wormit, and Dreuw, Mewes et al.(2015b)Mewes, Plasser, and Dreuw] These analyses are based on the state, transition and difference density matrices of the excited states; the theoretical background for such analysis is given in Chapter 7.12.
Descriptor |
Explanation |
Leading SVs$^2$ |
Largest NTO occupation numbers |
Sum of SVs$^2$ (Omega) |
|
E(h) |
Energy of hole NTO, |
E(p) |
Energy of particle NTO, |
PR_NTO |
NTO participation ratio |
Entanglement entropy (S_HE) |
|
Nr of entangled states (Z_HE) |
|
Renormalized S_HE/Z_HE |
Replace |
<r_h> [Ang] |
Mean position of hole |
<r_e> [Ang] |
Mean position of electron |
|<r_e - r_h>| [Ang] |
Linear e/h distance |
Hole size [Ang] |
RMS hole size: |
Electron size [Ang] |
RMS elec. size: |
RMS electron-hole separation [Ang] |
|
Covariance(r_h, r_e) [Ang^2] |
|
Correlation coefficient |
|
 equals the square of the norm of the 1TDM.
equals the square of the norm of the 1TDM. The transition-density (1TDM) based analyses include the construction and export of natural transition orbitals[Martin(2003)] (NTOs) and electron and hole densities,[Plasser et al.(2014b)Plasser, Wormit, and Dreuw] the evaluation of charge transfer numbers,[Plasser and Lischka(2012)] an analysis of exciton multipole moments,[Bäppler et al.(2014)Bäppler, Plasser, Wormit, and Dreuw, Plasser et al.(2015)Plasser, Thomitzni, Bäppler, Wenzel, Rehn, Wormit, and Dreuw, Mewes et al.(2015b)Mewes, Plasser, and Dreuw] and quantification of electron-hole entanglement.[Plasser(2016)] NTOs are obtained by singular value decomposition (SVD) of the 1TDM:
 |
 |
(11.13) | ||
 |
 |
(11.14) |
where  is diagonal matrix containing singular values and unitary matrices
is diagonal matrix containing singular values and unitary matrices  and
and  contain the respective particle and hole NTOs. Note that:
contain the respective particle and hole NTOs. Note that:
 |
(11.15) |
Furthermore, the formation and export of state-averaged NTOs, and the decomposition of the excited states into transitions of state-averaged NTOs are implemented.[Plasser et al.(2014b)Plasser, Wormit, and Dreuw] The difference and/or state densities can be exported themselves, as well as employed to construct and export natural orbitals, natural difference orbitals, and attachment and detachment densities.[Head-Gordon et al.(1995a)Head-Gordon, Graña, Maurice, and White] Furthermore, two measures of unpaired electrons are computed.[Head-Gordon(2003)] In addition, a Mulliken or Löwdin population analysis and an exciton analysis can be performed based on the difference/state densities. The main descriptors of the various analyses that are printed for each excited state are given in Tables 11.1 and 11.2. For a detailed description with illustrative examples, see Refs. Plasser:2014a and Plasser:2014b.
Descriptor |
Explanation |
n_u |
Number of unpaired electrons |
n_u,nl |
Number of unpaired electrons |
PR_NO |
NO participation ratio |
p_D and p_A |
Promotion number |
PR_D and PR_A |
D/A participation ratio |
<r_h> [Ang] |
Mean position of detachment density |
<r_e> [Ang] |
Mean position of attachment density |
|<r_e - r_h>| [Ang] |
Linear D/A distance |
Hole size [Ang] |
RMS size of detachment density |
Electron size [Ang] |
RMS size of attachment density |
To activate any excited-state analysis STATE_ANALYSIS has to be set to TRUE. For individual analyses there is currently only a limited amount of fine grained control. The construction and export of any type of orbitals is controlled by MOLDEN_FORMAT to export the orbitals as MolDen files, and NTO_PAIRS which specifies the number of important orbitals to print (note that the same keyword controls the number of natural orbitals, the number of natural difference orbitals, and the number of NTOs to be printed). Setting MAKE_CUBE_FILES to TRUE triggers the construction and export of densities in “cube file” format[Herbert(2015)] (see Section 11.5.4 for details). Activating transition densities in $plots will generate cube files for the transition density, the electron density, and the hole density of the respective excited states, while activating state densities or attachment/detachment densities will generate cube files for the state density, the difference density, the attachment density and the detachment density. Setting GUI = 2 will export data to the “.fchk” file and switches off the generation of cube files. The population analyses are controlled by POP_MULLIKEN and LOWDIN_POPULATION. Setting the latter to TRUE will enforce Löwdin population analysis to be employed, while by default the Mulliken population analysis is used.
Any MolDen or cube files generated by the excited state analyses can be found in the directory plots in the job’s scratch directory. Their names always start with a unique identifier of the excited state (the exact form of this human readable identifier varies with the excited state method). The names of MolDen files are then followed by either _no.mo, _ndo.mo, or _nto.mo depending on the type of orbitals they contain. In case of cube files the state identifier is followed by _dens, _diff, _trans, _attach, _detach, _elec, or _hole for state, difference, transition, attachment, detachment, electron, or hole densities, respectively. All cube files have the suffice .cube. In unrestricted calculations an additional part is added to the file name before .cube which indicates 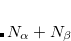 (_a) or
(_a) or  (_b) spin. The only exception is the state density for which _tot or _sd are added indicating the total or spin-density parts of the state density.
(_b) spin. The only exception is the state density for which _tot or _sd are added indicating the total or spin-density parts of the state density.
The _ctnum_atomic.om files created in the main directory serve as input for a charge transfer number analysis, as explained, e.g., in Refs. Plasser:2012, Mewes:2016. These files are processed by the external TheoDORE program () to create electron/hole correlation plots and to compute fragment based descriptors.
Note: (1) In Hermitian formalisms,  is a Hermitian conjugate of
is a Hermitian conjugate of  , but in non-Hermitian approaches, such as coupled-cluster theory, the two are slightly different. While for quantitative interstate properties both
, but in non-Hermitian approaches, such as coupled-cluster theory, the two are slightly different. While for quantitative interstate properties both  and
and  are computed, the qualitative trends in exciton properties derived from
are computed, the qualitative trends in exciton properties derived from  and
and  are very similar. Only one 1TDM is analyzed for EOM-CC.
are very similar. Only one 1TDM is analyzed for EOM-CC.
(2) In spin-restricted calculations, the libwfa module computes NTOs for the  block of transition density. Thus, when computing NTOs for the transitions between open-shell EOM-IP/EA states make sure to specify correct spin states. For example, use EOM_EA_ALPHA to visualize transitions involving the extra electron.
block of transition density. Thus, when computing NTOs for the transitions between open-shell EOM-IP/EA states make sure to specify correct spin states. For example, use EOM_EA_ALPHA to visualize transitions involving the extra electron.
NTO_PAIRS
Controls how many hole/particle NTO pairs and frontier natural orbital pairs and natural difference orbital pairs are computed for excited states.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:

Write
NTO/NO/NDO pairs per excited state.
RECOMMENDATION:
If activated (
), a minimum of two NTO pairs will be printed for each state. Increase the value of
if additional NTOs are desired. By default, one pair of frontier natural orbitals is computed for
.
 , sum of NTO occupation numbers
, sum of NTO occupation numbers 
















 and
and 
 and
and 




