13.9 The Adiabatic ALMO-EDA Method

Despite the huge success and usefulness of today’s most popular EDA methods, they still face some limitations in their capabilities. For instance, EDAs are usually performed at complex geometries that are obtained from unconstrained electronic structure calculations (e.g., optimized equilibrium geometries). For strongly interacting systems, close intermolecular contacts driven by POL and particularly CT often result in largely unfavorable FRZ interaction, which offers little physical insights besides indicating obviously substantial intermolecular overlap. Another limitation is that the conventional EDA methods often partitions a “single-point" interaction energy evaluated at a given geometry. Therefore, the influence of FRZ, POL and CT on the structural and vibrational properties of an intermolecular complex cannot be directly characterized.

Recently Mao et al. reformulated the original ALMO-EDA method in an adiabatic picture,[Mao et al.(2017)Mao, Horn, and Head-Gordon] where the term “adiabatic" is borrowed from spectroscopy and indicates that energy differences are evaluated at relaxed geometry on each potential energy surface (PES). In this scheme, the total binding energy (including monomer geometry distortions) is repartitioned into adiabatic FRZ, POL and CT terms:

$\begin{equation} \label{eq:ad_ EDA} \Delta E_{\mathrm{bind}} = \Delta E^{(\mathrm{ad})}_{\mathrm{frz}} + \Delta E^{(\mathrm{ad})}_{\mathrm{pol}} + \Delta E^{(\mathrm{ad})}_{\mathrm{ct}}. \end{equation}$

(13.13)

The adiabatic frozen interaction energy is given by the difference between the energy minimum of the frozen PES (on which the energy of each point is computed using the corresponding frozen wave function) and the sum of fully relaxed, non-interacting fragment energies:

$\begin{equation} \label{eq:ad_ FRZ} \Delta E^{(\mathrm{ad})}_{\mathrm{frz}} = E[\mathbf{P}_{\mathrm{frz}}^{(\mathrm{frz})}] - \sum _{A}E_{A}^{(0)}. \end{equation}$

(13.14)

Similarly, the adiabatic POL and CT terms can be obtained by performing geometry optimizations on the polarized (SCFMI) and fully relaxed (unconstrained SCF) PESs:

	$\displaystyle \Delta E^{(\mathrm{ad})}_{\mathrm{pol}}$	$\displaystyle = E[\mathbf{P}_{\mathrm{pol}}^{(\mathrm{pol})}] - E[\mathbf{P}_{\mathrm{frz}}^{(\mathrm{frz})}], \label{eq:ad_ POL}$		(13.15)
	$\displaystyle \Delta E^{(\mathrm{ad})}_{\mathrm{ct}}$	$\displaystyle = E[\mathbf{P}^{(\mathrm{full})}_{\mathrm{full}}] - E[\mathbf{P}_{\mathrm{pol}}^{(\mathrm{pol})}]. \label{eq:ad_ CT}$		(13.16)

With this method, the changes in monomer structures and intermolecular coordinates due to FRZ, POL and CT and the accompanied energetics are provided. Moreover, at the energy minimum (or other stationary points) on each PES, the other properties such as multipole points, vibrational frequencies and intensities can also be computed, therefore the effect of different intermolecular interaction components on them can also be characterized.

The geometry optimization on the frozen PES is facilitated by the analytical gradient of the frozen wave function energy implemented in Q-Chem. As for the geometry optimization on the polarized PES, the nuclear gradient of the SCFMI energy has the same form as that of the full SCF energy if the original ALMO model is used. These analytical gradients can also be used for finite difference calculations of harmonic frequencies by setting IDERIV = 1. We note that the analytical gradients of SCFMI calculations that use FERFs are not available yet, and SCFMI_MODE = 0 is required for computing the forces on the frozen and polarized PESs. Also, the current implementation of this method requires users to perform geometry optimization on the three PESs separately (see the example below) and evaluate the energy components by taking several Q-Chem outputs (including geometry optimizations for the monomers) together, which is probably not so convenient. We look forward to extending the functionality of this method and improving its implementation in the near future.

FRZ_GEOM

Compute forces on the frozen PES.

TYPE:

BOOLEAN

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not compute forces on the frozen PES.

TRUE

Compute forces on the frozen PES.

RECOMMENDATION:

Set it to TRUE when optimized geometry or vibrational frequencies on the frozen PES are desired.

POL_GEOM

Compute forces on the polarized (converged SCFMI) PES.

TYPE:

BOOLEAN

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not compute forces on the polarized PES.

TRUE

Compute forces on the polarized PES.

RECOMMENDATION:

Set it to TRUE when optimized geometry or vibrational frequencies on the polarized PES are desired.

Example 13.327 Geometry optimization of the ammonia-borane complex on the fully relaxed, polarized, and frozen potential energy surfaces successively.

$molecule
0 1
--
0 1
H       0.000000     0.000000     0.000000
H       0.000000     0.000000     1.629090
H       1.417687     0.000000     0.814543
N       0.473683    -0.370067     0.814542
--
0 1
N       3.494032    -1.531250     0.814538
H       3.967715    -1.901317    -0.000008
H       2.550028    -1.901319     0.814537
H       3.967715    -1.901317     1.629083
$end

$rem
   JOBTYPE          opt  !optimization on the fully relaxed PES
   GEN_SCFMAN       true
   METHOD           wb97x-d
   BASIS            6-31+g*
   XC_GRID          1
   THRESH           14  
   SCF_CONVERGENCE  9
   SCF_GUESS        fragmo
   SYMMETRY         false
   SYM_IGNORE       true
$end

@@@

$molecule
   read
$end

$rem
   JOBTYPE          opt 
   POL_GEOM         true !optimization on the polarized PES
   GEN_SCFMAN       true
   METHOD           wb97x-d
   BASIS            6-31+g*
   XC_GRID          1
   THRESH           14  
   SCF_CONVERGENCE  9
   SYMMETRY         false
   SYM_IGNORE       true
   SCFMI_MODE       0
$end

@@@

$molecule
   read
$end

$rem
   JOBTYPE          opt 
   FRZ_GEOM         true !optimization on the frozen PES
   GEN_SCFMAN       true
   METHOD           wb97x-d
   BASIS            6-31+g*
   XC_GRID          1
   THRESH           14  
   SCF_CONVERGENCE  9
   SYMMETRY         false
   SYM_IGNORE       true
   SCFMI_MODE       0
$end

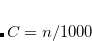Example 13.328 Geometry optimization of the CF $_3$ H $\cdots$ Cl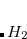 $^-$ complex on the frozen PES followed by a calculation for harmonic frequencies at the equilibrium geometry.

$molecule
-1 1
--
0 1
C         0.000000    0.000000    0.905509
H         0.000000    0.000000   -0.179815
F         1.250779    0.000000    1.406437
F        -0.625389   -1.083207    1.406437
F        -0.625389    1.083207    1.406437
--
-1 1
Cl        0.000000    0.000000   -2.664391
$end

$rem
   JOBTYPE                     opt 
   FRZ_GEOM                    true
   GEN_SCFMAN                  true
   METHOD                      wb97X-V
   BASIS                       def2-svpd
   XC_GRID                     000075000302
   THRESH                      14  
   SCF_CONVERGENCE             9
   SYMMETRY                    false
   SYM_IGNORE                  false
   SCFMI_MODE                  0
   GEOM_OPT_TOL_GRADIENT       100 
   GEOM_OPT_TOL_DISPLACEMENT   100 
   GEOM_OPT_TOL_ENERGY         10
   FD_MAT_VEC_PROD             false
$end

@@@

$molecule
   read
$end

$rem
   JOBTYPE           freq
   FRZ_GEOM          true
   GEN_SCFMAN        true
   METHOD            wb97X-V
   BASIS             def2-svpd
   XC_GRID           000075000302
   THRESH            14  
   SCF_CONVERGENCE   9
   SYMMETRY          false
   SYM_IGNORE        false
   IDERIV            1   
   SCFMI_MODE        0
   FD_MAT_VEC_PROD   false
$end

FALSE	Do not compute forces on the frozen PES.
TRUE	Compute forces on the frozen PES.

FALSE	Do not compute forces on the polarized PES.
TRUE	Compute forces on the polarized PES.