5.6 Range-Separated Hybrid Density Functionals
Whereas RSH functionals such as LRC- PBE are attempts to add 100% LR Hartree-Fock exchange with minimal perturbation to the original functional (PBE, in this example), other RSH functionals are of a more empirical nature and their range-separation parameters have been carefully parameterized along with all of the other parameters in the functional. These cases are functionals are discussed first, in Section 5.6.1, because their range-separation parameters should be taken as fixed. User-defined values of the range-separation parameter are discussed in Section 5.6.2, and Section 5.6.3 discusses a procedure for which an optimal, system-specific value of this parameter (
PBE are attempts to add 100% LR Hartree-Fock exchange with minimal perturbation to the original functional (PBE, in this example), other RSH functionals are of a more empirical nature and their range-separation parameters have been carefully parameterized along with all of the other parameters in the functional. These cases are functionals are discussed first, in Section 5.6.1, because their range-separation parameters should be taken as fixed. User-defined values of the range-separation parameter are discussed in Section 5.6.2, and Section 5.6.3 discusses a procedure for which an optimal, system-specific value of this parameter ( or
or 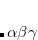 ) can be chosen for functionals such as LRC-
) can be chosen for functionals such as LRC- PBE or LRC-
PBE or LRC-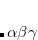 PBE.
PBE.
5.6.1 Semi-Empirical RSH Functionals
Semi-empirical RSH functionals for which the range-separation parameter should be considered fixed include the  B97,
B97,  B97X, and
B97X, and  B97X-D functionals developed by Chai and Head-Gordon;[Chai and Head-Gordon(2008a), Chai and Head-Gordon(2008b)]
B97X-D functionals developed by Chai and Head-Gordon;[Chai and Head-Gordon(2008a), Chai and Head-Gordon(2008b)]  B97X-V and
B97X-V and  B97M-V from Mardirossian and Head-Gordon;[Mardirossian and Head-Gordon(2014), Mardirossian and Head-Gordon(2016)] M11 from Peverati and Truhlar;[Peverati and Truhlar(2011b)]
B97M-V from Mardirossian and Head-Gordon;[Mardirossian and Head-Gordon(2014), Mardirossian and Head-Gordon(2016)] M11 from Peverati and Truhlar;[Peverati and Truhlar(2011b)]  B97X-D3,
B97X-D3,  M05-D, and
M05-D, and  M06-D3 from Chai and coworkers;[Lin et al.(2012)Lin, Tsai, Li, and Chai, Lin et al.(2013)Lin, Li, Mao, and Chai] and the screened exchange functionals N12-SX and MN12-SX from Truhlar and co-workers.[Peverati and Truhlar(2012d)] More recently, Mardirossian and Head-Gordon developed two RSH functionals,
M06-D3 from Chai and coworkers;[Lin et al.(2012)Lin, Tsai, Li, and Chai, Lin et al.(2013)Lin, Li, Mao, and Chai] and the screened exchange functionals N12-SX and MN12-SX from Truhlar and co-workers.[Peverati and Truhlar(2012d)] More recently, Mardirossian and Head-Gordon developed two RSH functionals,  B97X-V and
B97X-V and  B97M-V, via a combinatorial approach by screening over 100,000 possible functionals in the first case and over 10 billion possible functionals in the second case. Both of the latter functionals use the VV10 non-local correlation functional in order to improve the description of non-covalent interactions and isomerization energies.
B97M-V, via a combinatorial approach by screening over 100,000 possible functionals in the first case and over 10 billion possible functionals in the second case. Both of the latter functionals use the VV10 non-local correlation functional in order to improve the description of non-covalent interactions and isomerization energies.  B97M-V is a 12-parameter meta-GGA with 15% short-range exact exchange and 100% long-range exact exchange and is one of the most accurate functionals available through rung 4 of Jacob’s Ladder, across a wide variety of applications. This has been verified by benchmarking the functional on nearly 5000 data points against over 200 alternative functionals available in Q-Chem.[Mardirossian and Head-Gordon(2016)]
B97M-V is a 12-parameter meta-GGA with 15% short-range exact exchange and 100% long-range exact exchange and is one of the most accurate functionals available through rung 4 of Jacob’s Ladder, across a wide variety of applications. This has been verified by benchmarking the functional on nearly 5000 data points against over 200 alternative functionals available in Q-Chem.[Mardirossian and Head-Gordon(2016)]
5.6.2 User-Defined RSH Functionals
As pointed out in Ref. Dreuw:2003 and elsewhere, the description of charge-transfer excited states within density functional theory (or more precisely, time-dependent DFT, which is discussed in Section 7.3) requires full (100%) non-local HF exchange, at least in the limit of large donor–acceptor distance. Hybrid functionals such as B3LYP[Becke(1993), Stephens et al.(1994)Stephens, Devlin, Chabolowski, and Frisch] and PBE0[Adamo et al.(1999)Adamo, Scuseria, and Barone] that are well-established and in widespread use, however, employ only 20% and 25% HF exchange, respectively. While these functionals provide excellent results for many ground-state properties, they cannot correctly describe the distance dependence of charge-transfer excitation energies, which are enormously underestimated by most common density functionals. This is a serious problem in any case, but it is a catastrophic problem in large molecules and in non-covalent clusters, where TDDFT often predicts a near-continuum of spurious, low-lying charge transfer states.[Lange and Herbert(2007), Lange and Herbert(2009)] The problems with TDDFT’s description of charge transfer are not limited to large donor–acceptor distances, but have been observed at 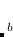 2 Å separation, in systems as small as uracil–(H
2 Å separation, in systems as small as uracil–(H O)
O) .[Lange and Herbert(2007)] Rydberg excitation energies also tend to be substantially underestimated by standard TDDFT.
.[Lange and Herbert(2007)] Rydberg excitation energies also tend to be substantially underestimated by standard TDDFT.
One possible avenue by which to correct such problems is to parameterize functionals that contain 100% HF exchange, though few such functionals exist to date. An alternative option is to attempt to preserve the form of common GGAs and hybrid functionals at short range (i.e., keep the 25% HF exchange in PBE0) while incorporating 100% HF exchange at long range, which provides a rigorously correct description of the long-range distance dependence of charge-transfer excitation energies, but aims to avoid contaminating short-range exchange-correlation effects with additional HF exchange. The separation is accomplished using the range-separation ansatz that was introduced in Section 5.3. In particular, functionals that use 100% HF exchange at long range ( in Eq. eq:RSHGGA) are known as “long-range-corrected” (LRC) functionals. An LRC version of PBE0 would, for example, have
in Eq. eq:RSHGGA) are known as “long-range-corrected” (LRC) functionals. An LRC version of PBE0 would, for example, have 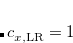 .
.
To fully specify an LRC functional, one must choose a value for the range separation parameter  in Eq. (). In the limit
in Eq. (). In the limit 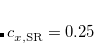 , the LRC functional in Eq. eq:RSHGGA reduces to a non-RSH functional where there is no “SR” or “LR”, because all exchange and correlation energies are evaluated using the full Coulomb operator,
, the LRC functional in Eq. eq:RSHGGA reduces to a non-RSH functional where there is no “SR” or “LR”, because all exchange and correlation energies are evaluated using the full Coulomb operator, 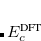 . Meanwhile the
. Meanwhile the 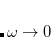 limit corresponds to a new functional,
limit corresponds to a new functional, 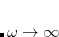 . Full HF exchange is inappropriate for use with most contemporary GGA correlation functionals, so the latter limit is expected to perform quite poorly. Values of
. Full HF exchange is inappropriate for use with most contemporary GGA correlation functionals, so the latter limit is expected to perform quite poorly. Values of 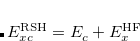 bohr
bohr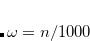 are likely not worth considering, according to benchmark tests.[Lange et al.(2008)Lange, Rohrdanz, and Herbert, Rohrdanz and Herbert(2008)]
are likely not worth considering, according to benchmark tests.[Lange et al.(2008)Lange, Rohrdanz, and Herbert, Rohrdanz and Herbert(2008)]
Evaluation of the short- and long-range HF exchange energies is straightforward,[Adamson et al.(1999)Adamson, Dombroski, and Gill] so the crux of any RSH functional is the form of the short-range GGA exchange functional, and several such functionals are available in Q-Chem. These include short-range variants of the B88 and PBE exchange described by Hirao and co-workers,[Iikura et al.(2001)Iikura, Tsuneda, Yanai, and Hirao, Song et al.(2007)Song, Hirosawa, Tsuneda, and Hirao] called 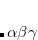 B88 and
B88 and 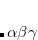 PBE in Q-Chem,[Richard and Herbert(2011)] and an alternative formulation of short-range PBE exchange proposed by Scuseria and co-workers,[Henderson et al.(2008)Henderson, Janesko, and Scuseria] which is known as
PBE in Q-Chem,[Richard and Herbert(2011)] and an alternative formulation of short-range PBE exchange proposed by Scuseria and co-workers,[Henderson et al.(2008)Henderson, Janesko, and Scuseria] which is known as  PBE. These functionals are available in Q-Chem thanks to the efforts of the Herbert group.[Rohrdanz and Herbert(2008), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] By way of notation, the terms “
PBE. These functionals are available in Q-Chem thanks to the efforts of the Herbert group.[Rohrdanz and Herbert(2008), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] By way of notation, the terms “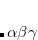 PBE”, “
PBE”, “ PBE”, etc., refer only to the short-range exchange functional,
PBE”, etc., refer only to the short-range exchange functional, 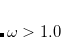 in Eq. eq:RSHGGA. These functionals could be used in “screened exchange” mode, as described in Section 5.3, as for example in the HSE03 functional,[Heyd et al.(2003)Heyd, Scuseria, and Ernzerhof] therefore the designation “LRC-
in Eq. eq:RSHGGA. These functionals could be used in “screened exchange” mode, as described in Section 5.3, as for example in the HSE03 functional,[Heyd et al.(2003)Heyd, Scuseria, and Ernzerhof] therefore the designation “LRC- PBE”, for example, should only be used when the short-range exchange functional
PBE”, for example, should only be used when the short-range exchange functional  PBE is combined with 100% Hartree-Fock exchange in the long range.
PBE is combined with 100% Hartree-Fock exchange in the long range.
In general, LRC-DFT functionals have been shown to remove the near-continuum of spurious charge-transfer excited states that appear in large-scale TDDFT calculations.[Lange et al.(2008)Lange, Rohrdanz, and Herbert] However, certain results depend sensitively upon the value of the range-separation parameter  ,[Lange et al.(2008)Lange, Rohrdanz, and Herbert, Rohrdanz and Herbert(2008), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert, Lange and Herbert(2009), Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth] especially in TDDFT calculations (Section 7.3) and therefore the results of LRC-DFT calculations must therefore be interpreted with caution, and probably for a range of
,[Lange et al.(2008)Lange, Rohrdanz, and Herbert, Rohrdanz and Herbert(2008), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert, Lange and Herbert(2009), Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth] especially in TDDFT calculations (Section 7.3) and therefore the results of LRC-DFT calculations must therefore be interpreted with caution, and probably for a range of  values. This can be accomplished by requesting a functional that contains some short-range GGA exchange functional (
values. This can be accomplished by requesting a functional that contains some short-range GGA exchange functional ( PBE or
PBE or 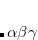 PBE, in the examples mentioned above), in combination with setting the $rem variable LRC_DFT = TRUE, which requests the addition of 100% Hartree-Fock exchange in the long-range. Basic job-control variables and an example can be found below. The value of the range-separation parameter is then controlled by the variable OMEGA, as shown in the examples below.
PBE, in the examples mentioned above), in combination with setting the $rem variable LRC_DFT = TRUE, which requests the addition of 100% Hartree-Fock exchange in the long-range. Basic job-control variables and an example can be found below. The value of the range-separation parameter is then controlled by the variable OMEGA, as shown in the examples below.
LRC_DFT
Controls the application of long-range-corrected DFT
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Do not apply long-range correction.
TRUE (or 1)
Add 100% long-range Hartree-Fock exchange to the requested functional.
RECOMMENDATION:
The $rem variable OMEGA must also be specified, in order to set the range-separation parameter.
OMEGA
Sets the range-separation parameter,
, also known as
, in functionals based on Hirao’s RSH scheme.
TYPE:
INTEGER
DEFAULT:
No default
OPTIONS:

Corresponding to
, in units of bohr
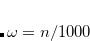
RECOMMENDATION:
None
COMBINE_K
Controls separate or combined builds for short-range and long-range K
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Build short-range and long-range K separately (twice as expensive as a global hybrid)
TRUE (or 1)
Build short-range and long-range K together (
as expensive as a global hybrid)
RECOMMENDATION:
Most pre-defined range-separated hybrid functionals in Q-Chem use this feature by default. However, if a user-specified RSH is desired, it is necessary to manually turn this feature on.
Example 5.47 Application of LRC-BOP to 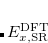 .
.
$comment
The value of omega is 0.47 by default but can
be overwritten by specifying OMEGA.
$end
$molecule
-1 2
O 1.347338 -0.017773 -0.071860
H 1.824285 0.813088 0.117645
H 1.805176 -0.695567 0.461913
O -1.523051 -0.002159 -0.090765
H -0.544777 -0.024370 -0.165445
H -1.682218 0.174228 0.849364
$end
$rem
EXCHANGE LRC-BOP
BASIS 6-31(1+,3+)G*
LRC_DFT TRUE
OMEGA 300 ! = 0.300 bohr**(-1)
$end
Rohrdanz et al.[Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] published a thorough benchmark study of both ground- and excited-state properties using the LRC- PBEh functional, in which the “h” indicates a short-range hybrid (i.e., the presence of some short-range HF exchange). Empirically-optimized parameters of
PBEh functional, in which the “h” indicates a short-range hybrid (i.e., the presence of some short-range HF exchange). Empirically-optimized parameters of 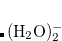 (see Eq. eq:RSHGGA) and
(see Eq. eq:RSHGGA) and 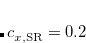 bohr
bohr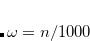 were obtained,[Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] and these parameters are taken as the defaults for LRC-
were obtained,[Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] and these parameters are taken as the defaults for LRC- PBEh. Caution is warranted, however, especially in TDDFT calculations for large systems, as excitation energies for states that exhibit charge-transfer character can be rather sensitive to the precise value of
PBEh. Caution is warranted, however, especially in TDDFT calculations for large systems, as excitation energies for states that exhibit charge-transfer character can be rather sensitive to the precise value of  .[Lange and Herbert(2009), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] In such cases (and maybe in general), the “tuning” procedure described in Section 5.6.3 is recommended.
.[Lange and Herbert(2009), Rohrdanz et al.(2009)Rohrdanz, Martins, and Herbert] In such cases (and maybe in general), the “tuning” procedure described in Section 5.6.3 is recommended.
Example 5.48 Application of LRC- PBEh to the
PBEh to the 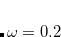 –
–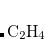 dimer at 5 Å separation.
dimer at 5 Å separation.
$comment
This example uses the "optimal" parameter set discussed above.
It can also be run by setting METHOD = LRC-wPBEh.
$end
$molecule
0 1
C 0.670604 0.000000 0.000000
C -0.670604 0.000000 0.000000
H 1.249222 0.929447 0.000000
H 1.249222 -0.929447 0.000000
H -1.249222 0.929447 0.000000
H -1.249222 -0.929447 0.000000
C 0.669726 0.000000 5.000000
C -0.669726 0.000000 5.000000
F 1.401152 1.122634 5.000000
F 1.401152 -1.122634 5.000000
F -1.401152 -1.122634 5.000000
F -1.401152 1.122634 5.000000
$end
$rem
EXCHANGE GEN
BASIS 6-31+G*
LRC_DFT TRUE
OMEGA 200 ! = 0.2 a.u.
CIS_N_ROOTS 4
CIS_TRIPLETS FALSE
$end
$xc_functional
C PBE 1.00
X wPBE 0.80
X HF 0.20
$end
Both LRC functionals and also the asymptotic corrections that will be discussed in Section 5.10.1 are thought to reduce self-interaction error in approximate DFT. A convenient way to quantify—or at least depict—this error is by plotting the DFT energy as a function of the (fractional) number of electrons,  , because
, because 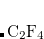 should in principle consist of a sequence of line segments with abrupt changes in slope (the so-called derivative discontinuity[Cohen et al.(2008)Cohen, Mori-Sánchez, and Yang, Mori-Sánchez and Cohen(2014)]) at integer values of
should in principle consist of a sequence of line segments with abrupt changes in slope (the so-called derivative discontinuity[Cohen et al.(2008)Cohen, Mori-Sánchez, and Yang, Mori-Sánchez and Cohen(2014)]) at integer values of  , but in practice these
, but in practice these 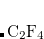 plots bow away from straight-line segments.[Cohen et al.(2008)Cohen, Mori-Sánchez, and Yang] Examination of such plots has been suggested as a means to adjust the fraction of short-range exchange in an LRC functional,[Autschbach and Srebro(2014)] while the range-separation parameter is tuned as described in Section 5.6.3.
plots bow away from straight-line segments.[Cohen et al.(2008)Cohen, Mori-Sánchez, and Yang] Examination of such plots has been suggested as a means to adjust the fraction of short-range exchange in an LRC functional,[Autschbach and Srebro(2014)] while the range-separation parameter is tuned as described in Section 5.6.3.
Example 5.49 Example of a DFT job with a fractional number of electrons. Here, we make the 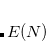 anion of fluoride by subtracting a fraction of an electron from the HOMO of F
anion of fluoride by subtracting a fraction of an electron from the HOMO of F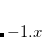 .
.
$comment
Subtracting a whole electron recovers the energy of F-.
Adding electrons to the LUMO is possible as well.
$end
$rem
EXCHANGE b3lyp
BASIS 6-31+G*
FRACTIONAL_ELECTRON -500 ! divide by 1000 to get the fraction, -0.5 here.
GEN_SCFMAN FALSE ! not yet available in new scf code
$end
$molecule
-2 2
F
$end
FRACTIONAL_ELECTRON
Add or subtract a fraction of an electron.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Use an integer number of electrons.

Add
electrons to the system.
RECOMMENDATION:
Use only if trying to generate
plots. If
, a fraction of an electron is removed from the system.
5.6.3 Tuned RSH Functionals
Whereas the range-separation parameters for the functionals described in Section 5.6.1 are wholly empirical in nature and should not be adjusted, for the functionals described in Section 5.6.2 some adjustment was suggested, especially for TDDFT calculations and for any properties that require interpretation of orbital energies, e.g., HOMO/LUMO gaps. This adjustment can be performed in a non-empirical, albeit system-specific way, by “tuning” the value of  in order to satisfy certain criteria that ought rigorously to be satisfied by an exact density functional.
in order to satisfy certain criteria that ought rigorously to be satisfied by an exact density functional.
System-specific optimization of  is based on the Koopmans condition that would be satisfied for the exact density functional, namely, that for an
is based on the Koopmans condition that would be satisfied for the exact density functional, namely, that for an  -electron molecule[Baer et al.(2010)Baer, Livshits, and Salzner]
-electron molecule[Baer et al.(2010)Baer, Livshits, and Salzner]
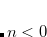 |
(5.24) |
In other words, the HOMO eigenvalue should be equal to minus the ionization energy (IE), where the latter is defined by a  SCF procedure.[van Gisbergen et al.(1996)van Gisbergen, Osinga, Gritsenko, van Leeuwen, Snijders, and Baerends, Wu et al.(2003)Wu, Ayers, and Yang] When an RSH functional is used, all of the quantities in Eq. eq:IP-tuning are
SCF procedure.[van Gisbergen et al.(1996)van Gisbergen, Osinga, Gritsenko, van Leeuwen, Snijders, and Baerends, Wu et al.(2003)Wu, Ayers, and Yang] When an RSH functional is used, all of the quantities in Eq. eq:IP-tuning are  -dependent, so this parameter is adjusted until the condition in Eq. eq:IP-tuning is met, which requires a sequence of SCF calculations on both the neutral and ionized species, using different values of
-dependent, so this parameter is adjusted until the condition in Eq. eq:IP-tuning is met, which requires a sequence of SCF calculations on both the neutral and ionized species, using different values of  . For proper description of charge-transfer states, Baer and co-workers[Baer et al.(2010)Baer, Livshits, and Salzner] suggest finding the value of
. For proper description of charge-transfer states, Baer and co-workers[Baer et al.(2010)Baer, Livshits, and Salzner] suggest finding the value of  that (to the extent possible) satisfies both Eq. eq:IP-tuning for the neutral donor molecule and its analogue for the anion of the acceptor species. Note that for a given approximate density functional, there is no guarantee that the IE condition can actually be satisfied for any value of
that (to the extent possible) satisfies both Eq. eq:IP-tuning for the neutral donor molecule and its analogue for the anion of the acceptor species. Note that for a given approximate density functional, there is no guarantee that the IE condition can actually be satisfied for any value of  , but in practice it usually can be, and published benchmarks suggest that this system-specific approach affords the most accurate values of IEs and TDDFT excitation energies.[Livshits and Baer(2007), Salzner and Baer(2009), Baer et al.(2010)Baer, Livshits, and Salzner] It should be noted, however, that the optimal value of
, but in practice it usually can be, and published benchmarks suggest that this system-specific approach affords the most accurate values of IEs and TDDFT excitation energies.[Livshits and Baer(2007), Salzner and Baer(2009), Baer et al.(2010)Baer, Livshits, and Salzner] It should be noted, however, that the optimal value of  can very dramatically with system size, e.g., it is very different for the cluster anion (H
can very dramatically with system size, e.g., it is very different for the cluster anion (H O)
O)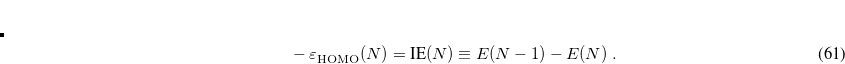 than it is for cluster (H
than it is for cluster (H O)
O) .[Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth]
.[Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth]
A script that optimizes  , called OptOmegaIPEA.pl, is located in the $QC/bin directory. The script scans
, called OptOmegaIPEA.pl, is located in the $QC/bin directory. The script scans  over the range 0.1–0.8 bohr
over the range 0.1–0.8 bohr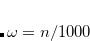 , corresponding to values of the $rem variable OMEGA in the range 100–800. See the script for the instructions how to modify the script to scan over a wider range. To execute the script, you need to create three inputs for a BNL job using the same geometry and basis set, for a neutral molecule (N.in), its anion (M.in), and its cation (P.in), and then run the command
, corresponding to values of the $rem variable OMEGA in the range 100–800. See the script for the instructions how to modify the script to scan over a wider range. To execute the script, you need to create three inputs for a BNL job using the same geometry and basis set, for a neutral molecule (N.in), its anion (M.in), and its cation (P.in), and then run the command
OptOmegaIPEA.pl >& optomega
which both generates the input files (N_*, P_*, M_*) and runs Q-Chem on them, writing the optimization output into optomega. This script applies the IE condition to both the neutral molecule and its anion, minimizing the sum of  for these two species. A similar script, OptOmegaIP.pl, uses Eq. eq:IP-tuning for the neutral molecule only.
for these two species. A similar script, OptOmegaIP.pl, uses Eq. eq:IP-tuning for the neutral molecule only.
Note: (i) If the system does not have positive EA, then the tuning should be done according to the IP condition only. The IP/EA script will yield an incorrect value of  in such cases.
in such cases.
(ii) In order for the scripts to work, one must specify SCF_FINAL_PRINT = 1 in the inputs. The scripts look for specific regular expressions and will not work correctly without this keyword.
Although the tuning procedure was originally developed by Baer and co-workers using the BNL functional,[Livshits and Baer(2007), Salzner and Baer(2009), Baer et al.(2010)Baer, Livshits, and Salzner] it has more recently been applied using functionals such as LRC- PBE (see, e.g., Ref. Uhlig:2014), and the scripts will work with functionals other than BNL.
PBE (see, e.g., Ref. Uhlig:2014), and the scripts will work with functionals other than BNL.
5.6.4 Tuned RSH Functionals Based on the Global Density-Dependent Condition
The value of range-separation parameter based on IP tuning procedure (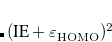 ) exhibits a troublesome dependence on system size.[Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth, Garrett et al.(2014)Garrett, Vazquez, Egri, Wilmer, Johnson, Robinson, and Isborn, Vazquez and Isborn(2015), Coons et al.(2016)Coons, You, and Herbert, Oviedo et al.(2016)Oviedo, Ilawe, and Wong] An alternative method to select
) exhibits a troublesome dependence on system size.[Uhlig et al.(2014)Uhlig, Herbert, Coons, and Jungwirth, Garrett et al.(2014)Garrett, Vazquez, Egri, Wilmer, Johnson, Robinson, and Isborn, Vazquez and Isborn(2015), Coons et al.(2016)Coons, You, and Herbert, Oviedo et al.(2016)Oviedo, Ilawe, and Wong] An alternative method to select  is the global density-dependent (GDD) tuning procedure,[Modrzejewski et al.(2013)Modrzejewski, Rajchel, Chalasinski, and Szczesniak] in which the optimal value
is the global density-dependent (GDD) tuning procedure,[Modrzejewski et al.(2013)Modrzejewski, Rajchel, Chalasinski, and Szczesniak] in which the optimal value
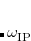 |
(5.25) |
is related to the average of the distance 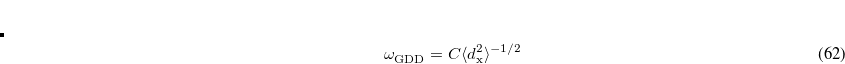 between an electron in the outer regions of a molecule and the exchange hole in the region of localized valence orbitals. The quantity
between an electron in the outer regions of a molecule and the exchange hole in the region of localized valence orbitals. The quantity 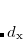 is an empirical parameter for a given LRC functional, which was determined for LRC-
is an empirical parameter for a given LRC functional, which was determined for LRC- PBE (
PBE (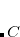 ) and LRC-
) and LRC- PBEh (
PBEh (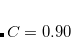 ) using the def2-TZVPP basis set.[Modrzejewski et al.(2013)Modrzejewski, Rajchel, Chalasinski, and Szczesniak] (A slightly different value,
) using the def2-TZVPP basis set.[Modrzejewski et al.(2013)Modrzejewski, Rajchel, Chalasinski, and Szczesniak] (A slightly different value, 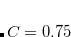 , was determined for Q-Chem’s implementation of LRC-
, was determined for Q-Chem’s implementation of LRC- PBE.[Lao and Herbert()]) Since LRC-
PBE.[Lao and Herbert()]) Since LRC- PBE(
PBE(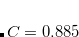 ) provides a better description of polarizabilities in polyacetylene as compared to
) provides a better description of polarizabilities in polyacetylene as compared to 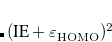 [Hapka et al.(2014)Hapka, Rajchel, Modrzejewski, Chałasiǹski, and Szczȩśniak], it is anticipated that using
[Hapka et al.(2014)Hapka, Rajchel, Modrzejewski, Chałasiǹski, and Szczȩśniak], it is anticipated that using 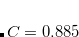 in place of
in place of 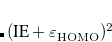 may afford more accurate molecular properties, especially in conjugated systems. GDD tuning of an RSH functional is involving by setting the $rem variable OMEGA_GDD = TRUE. The electron density is obviously needed to compute
may afford more accurate molecular properties, especially in conjugated systems. GDD tuning of an RSH functional is involving by setting the $rem variable OMEGA_GDD = TRUE. The electron density is obviously needed to compute 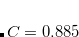 in Eq. eq:wgdd and this is accomplished using the converged SCF density computed using the RSH functional with the value of
in Eq. eq:wgdd and this is accomplished using the converged SCF density computed using the RSH functional with the value of  given by the $rem variable OMEGA. The value of
given by the $rem variable OMEGA. The value of 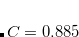 therefore depends, in principle, upon the value of OMEGA, although in practice it is not very sensitive to this value.
therefore depends, in principle, upon the value of OMEGA, although in practice it is not very sensitive to this value.
OMEGA_GDD
Controls the application of
tuning for long-range-corrected DFT
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Do not apply
tuning.
TRUE (or 1)
Use
tuning.
RECOMMENDATION:
The $rem variable OMEGA must also be specified, in order to set the initial range-separation parameter.
OMEGA_GDD_SCALING
Sets the empirical constant
in
tuning procedure.
TYPE:
INTEGER
DEFAULT:
885
OPTIONS:

Corresponding to
.
RECOMMENDATION:
The quantity
= 885 was determined by Lao and Herbert in Ref. Lao:2018 using LRC-
PBE and def2-TZVPP augmented with diffuse functions on non-hydrogen atoms that are taken from Dunning’s aug-cc-pVTZ basis set.
Example 5.50 Sample input illustrating a calculation to determine the  value for LRC-
value for LRC- PBE based on the
PBE based on the 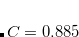 tuning procedure.
tuning procedure.
$comment
The initial omega value has to set.
$end
$rem
exchange gen
basis aug-cc-pvdz
lrc_dft true
omega 300
omega_gdd true
$end
$xc_functional
x wPBE 1.0
c PBE 1.0
$end
$molecule
0 1
O -0.042500 0.091700 0.110000
H 0.749000 0.556800 0.438700
H -0.825800 0.574700 0.432500
$end