13.13 Energy Decomposition Analysis based on SAPT/cDFT

Many schemes for decomposing quantum chemical calculations of intermolecular interaction energies into physically meaningful components can be found in the literature, but the definition of the charge-transfer (CT) contribution has proven particularly vexing to define in a satisfactory way and typically depends strongly on the choice of basis set,[Ronca et al.(2014)Ronca, Belpassi, and Tarantelli, Řezáč and de la Lande(2015), Lao and Herbert(2016)] because as virtual orbitals on monomer $A$ start to extend significantly over monomer $B$ 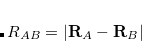as the basis set approaches completeness, the distinction between polarization (excitations localized on $A$ , introduced by the perturbing influence of $B$ ) 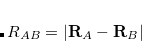and CT (excitations from $A$ to $B$ ) 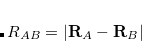becomes blurred.[Lao and Herbert(2016)] This ambiguity renders orbital-dependent definitions of CT highly dependent on the choice of atomic orbital basis set. On the other hand, constrained density functional theory (cDFT, Section 5.13), where a CT-free reference state can be defined based on “promolecule” densities, affords a definition of CT that is scarcely dependent on the basis set and is in accord with chemical intuition in simple cases.[Lao and Herbert(2016)]

For intermolecular interactions, the cDFT definition of CT can be combined with a definition of the remaining components of the interaction energy (electrostatics, induction, Pauli repulsion, and van der Waals interactions) based on symmetry-adapted perturbation theory (SAPT, Section 13.11). In traditional SAPT, the CT interaction energy resides within the induction energy (also known as the polarization energy), which is therefore itself highly dependent upon the basis set. However, using cDFT to define the CT component and subtracting this out of the SAPT induction energy, both the CT and the remaining induction energies are largely independent of basis set.[Lao and Herbert(2016)] SAPT/cDFT therefore provides a stable and physically-motivated energy decomposition, which can be invoked by setting the $rem variable SAPT_CDFT_EDA = TRUE in a SAPT calculation. A $cdft section must be set to specify the monomer charges and spins for the cDFT calculation.

While the cDFT definition of CT exhibits only a very mild basis-set dependence, its quantitative details do depend upon how the charge constraints in cDFT are defined relative to fragment populations (Section 5.13). For SAPT/cDFT, both atomic Becke[Becke(1988a)] and fragment-based Hirshfeld[Řezáč and de la Lande(2015)] (FBH) charge partitioning methods are available. The former involves construction of atomic cell functions that amount to smoothed Voronoi polyhedra centered about each atom. 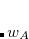A switching function defines the atomic cell of atom $a$ , and falls rapidly from $\approx 1$ near the nucleus for atom $a$ , to $\approx 0$ near any other nucleus. Becke[Becke(1988a)] defined atomic cell functions $P_{a}(\textbf{r})$ that are products of switching functions and that can be used to define the cDFT integration weight for monomer $A$ by summing over atoms $a\in A$ :

$\begin{equation} \label{eq:becky_ weights} w^{\rm Becke}_{A}(\textbf{r}) = \frac{ \sum _{a\in A} P_{a}(\textbf{r}) }{ \sum _ b P_{b}(\textbf{r}) } \; . \end{equation}$

(13.39)

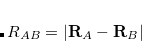The sum in the denominator runs over all atoms in both monomers, $A$ and $B$ . Becke populations, however, are rooted in a somewhat arbitrarily-defined topology, based in part on assumed atomic radii, whereas FBH partitioning derives physical significance from isolated monomer densities $\widetilde{\rho }^{}_ A(\mathbf{r})$ and $\widetilde{\rho }^{}_ B(\mathbf{r})$ . The cDFT weight function for monomer $A$ is[Řezáč and de la Lande(2015)]

$\begin{equation} \label{eq:fbh_ weights} w_ A^{\rm FBH}(\mathbf{r}) = \frac{ \widetilde{\rho }^{}_ A(\mathbf{r}) }{ \widetilde{\rho }^{}_ A(\mathbf{r}) + \widetilde{\rho }^{}_ B(\mathbf{r}) } \; , \end{equation}$

(13.40)

which is the same “stockholder” scheme used to define atomic Hirshfeld populations (Section 11.2.1), but applied here to the entire monomer. In the language of cDFT, the denominator in this expression would be called the promolecule density for the dimer $A + B$ . In order to set a molecular fragment constraint, simply retain the existing syntax in the $cdft input section (as described in Section 5.13) and specify all atoms within a given molecular fragment.

To perform SAPT/cDFT energy decomposition analysis, the user must request a normal SAPT calculation and in addition set SAPT_CDFT_EDA = TRUE. Users of this method are asked to cite Ref. Lao:2016b.

SAPT_CDFT_EDA

Request a SAPT/cDFT energy decomposition analysis

TYPE:

BOOLEAN

DEFAULT:

FALSE

OPTIONS:

TRUE

Run a SAPT/cDFT calculation.

FALSE

Do not run SAPT/cDFT.

RECOMMENDATION:

None

CDFT_POP

Sets the charge partitioning scheme for cDFT in SAPT/cDFT

TYPE:

STRING

DEFAULT:

FBH

OPTIONS:

FBH

Fragment-Based Hirshfeld partitioning

BECKE

Atomic Becke partitioning

RECOMMENDATION:

None

Example 13.334 Energy decomposition analysis for the water dimer using AO-SAPT+aiD3/cDFT.

$comment
   a $cdft input section must be set to specify the monomer 
   charges and spins for the cDFT calculation.
$end

$rem
   SYM_IGNORE         true
   EXCHANGE           gen
   BASIS              aug-cc-pvdz
   XPOL               true ! must be set to true for sapt jobs too
   XPOL_MPOL_ORDER    gas ! gas or charges
   XPOL_OMEGA         true
   XPOL_PRINT         3
   SAPT_PRINT         3
   SAPT               true
   SAPT_AO            true
   SAPT_ORDER         2       ! can be set to 1, ELST or RSPT
   SAPT_BASIS         dimer ! monomer, dimer (if only 2 monomers), or projected
   SAPT_DISP_CORR     true
   SAPT_DISP_VERSION  3
   LRC_DFT            true
   SAPT_CDFT_EDA      true
   CDFT_POP           fbh ! Fragment-Based Hirshfeld (FBH) charge partitioning
$end

$xc_functional
   x   wPBE   1.0
   c    PBE   1.0
$end

$lrc_omega
   500
   500
$end

$cdft
   0
   1 1 3
   0
   1 1 3 s
$end

$molecule
0 1
--
   0 1
   O   -0.702196054  -0.056060256   0.009942262
   H   -1.022193224   0.846775782  -0.011488714
   H    0.257521062   0.042121496   0.005218999
--
0 1
   O    2.220871067   0.026716792   0.000620476
   H    2.597492682  -0.411663274   0.766744858
   H    2.593135384  -0.449496183  -0.744782026
$end

FBH	Fragment-Based Hirshfeld partitioning
BECKE	Atomic Becke partitioning