13.14 The Many-Body Expansion Method

13.14.1 Theory and Implementation Details

The many-body expansion (MBE) for a system of $N$ monomers is given by

$\begin{equation} \label{eq:mb} E = \sum _{I=1}^ N\mbox{$E_{I}^{}$}+\sum _{I}^{N}\sum _{J>I}^{N}\mbox{$\Delta E_{IJ}^{}$}+ \\ \sum _{I}^{N}\sum _{J>I}^{N}\sum _{K>J}^{N}\mbox{$\Delta E_{IJK}^{}$} + \\ \cdots , \end{equation}$

(13.41)

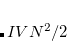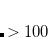
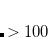
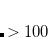
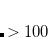
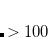
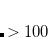
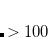
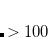
in which $E_{I}$ represents the energy of monomer $I$ , $\Delta E_{IJ}$ = $E_{IJ}$ $-$ $E_{I}$ $-$ $E_{J}$ is a two-body correction for dimer $IJ$ , and $\Delta E_{IJK}$ = $E_{IJK}$ $-$ $\Delta E_{IJ}$ $-$ $\Delta E_{IK}$ $-$ $\Delta E_{JK}$ $-$ $E_{I}$ $-$ $E_{J}$ $-$ $E_{k}$ is a three-body correction for trimer $IJK$ , etc. In a large system and/or a large basis set, truncation of this expression at the two- or three-body level may dramatically reduce the amount of computer time that is required to compute the energy. 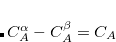Convergence of the MBE can be accelerated by embedding the monomer ( $E_{I}$ ), dimer ( $E_{IJ}$ ), trimer ( $E_{IJK}$ ), $\ldots$ calculations in some representation of the electrostatic potential of the rest of the system. A simple means to do this is via atom-centered point charges that could be obtained when the $E_ I$ terms are calculated; this is the so-called electrostatically-embedded many-body expansion (EE-MBE).[Dahlke and Truhlar(2007), Richard et al.(2014a)Richard, Lao, and Herbert, Richard et al.(2014b)Richard, Lao, and Herbert, Lao et al.(2016)Lao, Liu, Richard, and Herbert] Alternatively, since the monomer electron densities are available from the $E_ I$ terms as well, one could use these densities to compute the actual monomer–monomer Coulomb interactions, and this forms the basis of the fragment molecular orbital (FMO) method.[Kitaura et al.(1999)Kitaura, Ikeo, Asada, Nakano, and Uebayasi, Fedorov and Kitaura(2007)] In particular, the “bodies” (fragments) cannot be covalently bonded to one another, and therefore this is a method appropriate for non-covalent clusters of molecules. Moreover, individual subsystem calculations have been parallelized across processors using MPI, hence the present implementation is using the real power of the MBE. Analytic gradients are also available for MBE and EE-MBE, but not FMO.

It is well known that the interaction energies of non-covalent clusters are usually overestimated (often substantially) owing to basis-set superposition error (BSSE), which disappears only very slowly as the basis sets approach completeness. The widely used Boys–Bernardi counterpoise (CP) procedure corrects for this by computing all energies (including cluster and monomers) using the cluster basis set. 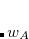(Note, however, that basis-set extrapolation is still necessary for high-quality binding energies; in $(\rm H_2O)_6$ , for example, a CP-corrected MP2/aug-cc-pVQZ calculation is still $\approx 1$ kcal/mol from the MP2 basis-set limit.[Richard et al.(2013a)Richard, Lao, and Herbert] Fortunately, the MBE allows for use of large basis sets in order to perform basis-set extrapolations in sizable clusters.[Richard et al.(2013a)Richard, Lao, and Herbert, Richard et al.(2013b)Richard, Lao, and Herbert]) Two low-cost CP corrections that are consistent with an $n$ -body expansion have been proposed: the many-body CP correction, MBCP( $n$ ),[Richard et al.(2013a)Richard, Lao, and Herbert, Richard et al.(2013b)Richard, Lao, and Herbert] and the $n$ -body Valiron-Mayer function counterpoise correction, VMFC( $n$ ).[Kamiya et al.(2008)Kamiya, Hirata, and Valiev] The two approaches are equivalent for $n=2$ but the MBCP( $n$ ) method requires far fewer subsystem calculations starting at $n=3$ and is thus significantly cheaper, while affording very similar results as compared to VMFC( $n$ ).[Richard et al.(2013a)Richard, Lao, and Herbert, Richard et al.(2013b)Richard, Lao, and Herbert]

Q-Chem’s implementation of the EE-MBE( $n$ ) approach (electrostatically-embedded $n$ -body expansion) is designed to use $mbe_charges section to specify embedding charges. As such, a MBE calculation is requested by setting MANY_BODY_INT = TRUE. The variable MBE_EMBEDDING = CHARGES/GAS sets the MBE calculations with or without using embedding charges. The variable MBE_ORDER sets the truncation order, $n$ . As an alternative to point charges, density embedding is also available, in which Coulomb interactions are computed between proper monomer electron densities. The MBE with density embedding is equivalent to the original version of the fragment molecular orbital (FMO).[Kitaura et al.(1999)Kitaura, Ikeo, Asada, Nakano, and Uebayasi] (Many subsequent modifications to the FMO algorithm have been introduced[Fedorov and Kitaura(2007), Fedorov and Kitaura(2009)] but are not yet available in Q-Chem. These include, in particular, the option to use point charges or approximate electron repulsion integrals to compute the Coulomb interactions between distant monomers,[Nakano et al.(2002)Nakano, Kaminuma, Sato, Fukuzawa, Akiyama, Uebayasi, and Kitaura, Fedorov et al.(2010)Fedorov, Slipchenko, and Kitaura] which actually makes FMO more like EE-MBE at long range.) This density-embedded version of FMO is available in Q-Chem by setting XPOL = TRUE, XPOL_MPOL_ORDER = DENSITY, and FRAG_MOL_ORB = TRUE. The variable FMO_ORDER sets the truncation order, $n$ . The MBE version of BSSE is requested by setting MANY_BODY_BSSE = MBCP or VMFC. The variable MBE_BSSE_ORDER sets the truncation order, $n$ .

Researchers who use Q-Chem’s MBE code are asked to cite Ref. Richard:2014a,Lao:2016a and—if the MBCP( $n$ ) method is used—to cite Ref. Richard:2013a as well.

13.14.2 Job Control and Examples

The following $rem variables control MBE jobs.

MANY_BODY_INT

Perform a MBE calculation.

TYPE:

BOOLEAN

DEFAULT:

FALSE

OPTIONS:

TRUE

Perform a MBE calculation.

FALSE

Do not perform a MBE calculation.

RECOMMENDATION:

NONE

MBE_ORDER

Controls the truncation order $n$ for MBE.

TYPE:

INTEGER

DEFAULT:

2

OPTIONS:

$N$

Order of MBE

RECOMMENDATION:

MBE can be performed up to fifth order.

MBE_EMBEDDING

Controls the type of MBE calculations.

TYPE:

STRING

DEFAULT:

GAS

OPTIONS:

GAS

MBE without charge embedding.

CHARGES

MBE with charge embedding.

RECOMMENDATION:

NONE.

MANY_BODY_BSSE

Controls the type of many-body BSSE corrections.

TYPE:

STRING

DEFAULT:

MBCP

OPTIONS:

MBCP

Use many-body counterpoise correction.

VMFC

Use Valiron-Mayer function counterpoise correction.

RECOMMENDATION:

NONE.

MBE_BSSE_ORDER

Controls the order of many-body BSSE corrections.

TYPE:

INTEGER

DEFAULT:

2

OPTIONS:

$n$

Order of many-body BSSE corrections

RECOMMENDATION:

MBCP and VMFC can be performed up to fourth order.

FRAG_MOL_ORB

Perform a FMO calculation.

TYPE:

BOOLEAN

DEFAULT:

FALSE

OPTIONS:

TRUE

Perform a FMO calculation.

FALSE

Do not perform a FMO calculation.

RECOMMENDATION:

NONE

FMO_ORDER

Controls the truncation order $n$ for FMO.

TYPE:

INTEGER

DEFAULT:

NONE

OPTIONS:

$N$

Order of FMO

RECOMMENDATION:

FMO can be performed up to third order.

Example 13.335 Example showing a 3-body EE-MBE calculation using TIP3P charges.

$rem
   SYM_IGNORE        true
   METHOD            B3LYP
   BASIS             cc-pVDZ
   MANY_BODY_INT     true
   MBE_ORDER         3
   MBE_EMBEDDING     charges
   THRESH            14
   SCF_CONVERGENCE   7
$end

$molecule
0 1
--
   0 1
   O -1.126149 -1.748387 -0.423240
   H -0.234788 -1.493897 -0.661862
   H -1.062789 -2.681331 -0.218819
--
   0 1
   O -0.254210 1.611495 -1.293845
   H -1.001520 1.163510 -1.690129
   H -0.153399 2.411746 -1.809248
--
   0 1
   O 1.694541 -0.226287 1.705739
   H 0.785920 0.073487 1.677909
   H 2.047134 0.150917 2.511706
--
   0 1
   O -0.864533 0.522472 1.218817
   H -0.694120 1.093542 0.469789
   H -1.131418 -0.310426 0.829702
$end

$mbe_charges
  -0.834
   0.417
   0.417
  -0.834
   0.417
   0.417
  -0.834
   0.417
   0.417
  -0.834
   0.417
   0.417
$end

Example 13.336 Example showing a 3-body MBCP calculation.

$rem
   SYM_IGNORE        true
   METHOD            B3LYP
   BASIS             cc-pVDZ
   MANY_BODY_BSSE    mbcp
   MBE_BSSE_ORDER    3
   THRESH            14
   SCF_CONVERGENCE   7
$end

$molecule
0 1
--
   0 1
   O -1.126149 -1.748387 -0.423240
   H -0.234788 -1.493897 -0.661862
   H -1.062789 -2.681331 -0.218819
--
   0 1
   O -0.254210 1.611495 -1.293845
   H -1.001520 1.163510 -1.690129
   H -0.153399 2.411746 -1.809248
--
   0 1
   O 1.694541 -0.226287 1.705739
   H 0.785920 0.073487 1.677909
   H 2.047134 0.150917 2.511706
--
   0 1
   O -0.864533 0.522472 1.218817
   H -0.694120 1.093542 0.469789
   H -1.131418 -0.310426 0.829702
$end

Example 13.337 Example showing a 3-body FMO calculation.

$rem
   SYM_IGNORE        true
   METHOD            B3LYP
   BASIS             cc-pVDZ
   XPOL              true 
   XPOL_MPOL_ORDER   density
   FRAG_MOL_ORB      true
   FMO_ORDER         3
   THRESH            14
   SCF_CONVERGENCE   7
$end

$molecule
0 1
--
   0 1
   O -1.126149 -1.748387 -0.423240
   H -0.234788 -1.493897 -0.661862
   H -1.062789 -2.681331 -0.218819
--
   0 1
   O -0.254210 1.611495 -1.293845
   H -1.001520 1.163510 -1.690129
   H -0.153399 2.411746 -1.809248
--
   0 1
   O 1.694541 -0.226287 1.705739
   H 0.785920 0.073487 1.677909
   H 2.047134 0.150917 2.511706
--
   0 1
   O -0.864533 0.522472 1.218817
   H -0.694120 1.093542 0.469789
   H -1.131418 -0.310426 0.829702
$end

TRUE	Perform a MBE calculation.
FALSE	Do not perform a MBE calculation.

GAS	MBE without charge embedding.
CHARGES	MBE with charge embedding.

MBCP	Use many-body counterpoise correction.
VMFC	Use Valiron-Mayer function counterpoise correction.

TRUE	Perform a FMO calculation.
FALSE	Do not perform a FMO calculation.