13.15 Ab Initio Frenkel Davydov Exciton Model (AIFDEM)

13.15.1 Theory

A fairly old idea for describing the (potentially delocalized) excited states of molecular crystals, or more generally noncovalent assemblies or aggregates of (weakly) electronically-coupled chromophores, is the so called Frenkel-Davydov Exciton model. In such a model, a collective excitation of the entire aggregate is expressed as a linear combination of excitations that are localized on molecular sites. The 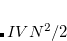$I$ th excited state, $|\Xi _ I\rangle$ , is thus written

$\begin{equation} \label{eq:AIFDEM_ direct_ pdt} |\Xi _ I\rangle =\sum _ n^{\rm sites} \; \sum _ i^{\rm states} K_ n^{Ii} |\Psi _ n^ i\rangle \prod _{m\neq n}|\Psi _ m\rangle \; , \end{equation}$

(13.42)

where $|\Psi _ n^ i\rangle$ is the $i$ th excited state of the $n$ th molecular fragment and $|\Psi _ m\rangle$ is the ground-state wave function of the $m$ th fragment. Eigenstates and energies are found by constructing and diagonalizing the electronic Hamiltonian matrix in this direct product, “exciton-site basis”.

In the ab initio Frenkel-Davydov exciton model (AIFDEM) developed by Morrison and Herbert,[Morrison et al.(2014)Morrison, You, and Herbert, Morrison and Herbert(2015)] the ground-state wave functions in Eq. eq:AIFDEM_direct_pdt are single Slater determinants (obtained from SCF calculations on isolated fragments), and the fragment excited-state wave functions are linear combinations of singly-excited determinants:

$\begin{equation} |\Psi _{\! A}^\ast \rangle = \sum _{ia} C^{ia}|\Phi _{\! A}^{ia}\rangle \; . \end{equation}$

(13.43)

The AIFDEM approach computes elements of the exact Hamiltonian,

$\begin{equation} \label{eq:AIFDEM_ H} \langle \Psi _{\! A}^\ast \Psi _{\! B}\Psi _{\! C}\ldots |\hat{H}|\Psi _{\! A}\Psi _{\! B}^\ast \Psi _{\! C}\ldots \rangle = \sum _{ia \sigma }\sum _{kb \tau } C^{i a }_{\sigma } C^{kb}_{\tau }\langle \Phi ^{ia}_{\! A}\Phi _{\! B} \Phi _{\! C}\ldots |\hat{H}|\Phi _{\! A}\Phi ^{k b}_{\! B}\Phi _{\! C}\ldots \rangle \; . \end{equation}$

(13.44)

In particular, no dipole-coupling approximation is made (as is often invoked in simple exciton models). Such an approximation may be valid for well-separated chromophores but likely less so for tightly-packed chromophores in a molecular crystal. Overlap matrices

$\begin{equation} \label{eq:AIFDEM_ S} \left\langle \Psi _{\! A}^\ast \Psi _{\! B}\Psi _{\! C}\ldots |\Psi _{\! A}\Psi _{\! B}^\ast \Psi _{\! C} \ldots \right\rangle = \sum _{ia \sigma }\sum _{kb \tau } C^{i a}_{\sigma } C^{kb}_{\tau } \langle \Phi ^{ia}_{\! A}\Phi _{\! B}\Phi _{\! C}\ldots |\Phi _{\! A}\Phi ^{k b}_{\! B}\Phi _{\! C}\ldots \rangle \end{equation}$

(13.45)

are also required because molecular orbitals located on different fragments are not orthogonal to one another. In order to reduce the number of terms in Eqs. eq:AIFDEM_H and eq:AIFDEM_S, the fragment excited states are transformed into the natural transition orbital (NTO) basis (see Section 7.12.2) and then the corresponding orbitals transformation (Section 11.16.2.2) is used to compute matrix elements between non-orthogonal Slater determinants. The size of the exciton-site basis is sufficiently small such that eigenvectors and energies of the exciton Hamiltonian can be printed and saved to scratch files. Transition dipole moments between the ground state and the first ten excited states of the exciton Hamiltonian are also computed.

The cost to compute each matrix element scales with the size of the supersystem (somewhere between quadratic and quartic with monomer size), since all fragments must be included in the direct products. To reduce this scaling, a physically-motivated charge embedding scheme was introduced[Morrison and Herbert(2015)] that only treats the excited fragments, and neighbors within a user-specified distance threshold, with full QM calculation, while the other ground state fragment interactions are approximated by point charges. (The nature of the point charges is controlled by the $rem variable XPOL_CHARGE_TYPE.) In general, inclusion of neighboring fragments in the QM part of the matrix element evaluation does not seem to significantly improve the accuracy and diminishes the cost savings of the charge-embedding procedure. Therefore, the minimal “ 0 Å” threshold, where only the excited fragments are described at a QM level, can be considered optimal. Charge embedding with the minimal threshold affords an algorithm that scales as $F^2 \times \mathcal{O}(n_{\text {pair}}^{2-4})$ , where $F$ is the number of fragments and $n_{\text {pair}}$ is the size of a pair of fragments.

The exciton-site basis can be expanded to include higher-lying fragment excited states which affords the wave function increased variational flexibility, and can significantly improve the accuracy for polar systems and delocalized excited states. The number of fragment excited states included in the basis is specified by the CIS_N_ROOTS keyword, which must be $\ge 1$ . A cost effective means of including polarization effects is to use the XPol method to compute fragment ground states, see Section 13.10 and associated job controls. Fragment excited states are then computed using the XPol-polarized MOs. Charge transfer-type states of the form $|\Phi _{\! A}^+\Phi _{\! B}^-\Phi _{\! C}\ldots \rangle$ , where $\Phi _{\! A}^{\pm }$ are cationic or anionic determinants from unrestricted SCF calculations on the isolated fragments, can also be included in the basis.

The exciton-site basis states are spin-adapted to form proper 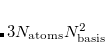$\Hat {S}^2$ eigenstates. Their multiplicity determines that of the target excited state and this must be specified by setting CIS_SINGLETS or CIS_TRIPLETS to TRUE. The number of terms included in Eqs. eq:AIFDEM_H and eq:AIFDEM_S can be rationally truncated at some fraction of the norm of the fragment NTO amplitudes, in order to reduce cost at the expense of accuracy, although the approximation is controllable by means of the truncation threshold. Computation time scales approximately quadratically with the number of terms and a threshold of about 85% has been found to maintain acceptable accuracy for organic molecules with reasonable cost. The fragment orbitals and excited states may be computed with any SCF and single-excitation theory, including DFT and TDDFT, however the coupling matrix elements are always computed with a CIS-like Hamiltonian with no DFT exchange-correlation. Both OpenMP and MPI parallel implementations are available; the former distributes two-electron integral computation across cores in a node as in a traditional excited-state calculation, the latter can distribute matrix element evaluations across hundreds of cores with minimal overhead.

Note: Symmetry should be turned off for AIFDEM calculations.

13.15.2 Job Control

AIFDEM

Perform an AIFDEM calculation.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not perform an AIFDEM calculation.

TRUE

Perform an AIFDEM calculation.

RECOMMENDATION:

False

AIFDEM_NTOTHRESH

Controls the number of NTOs that are retained in the exciton-site basis states.

TYPE:

INTEGER

DEFAULT:

99

OPTIONS:

$n$

Threshold percentage of the norm of fragment NTO amplitudes.

RECOMMENDATION:

A threshold of $85 \%$ gives a good trade-off of computational time and accuracy for organic molecules.

AIFDEM_EMBED_RANGE

Specifies the size of the QM region for charge embedding

TYPE:

INTEGER

DEFAULT:

FULL_QM

OPTIONS:

FULL_QM

No charge embedding.

0

Treat only excited fragments with QM.

$n$

Range (Å) from excited fragments within which to treat other fragments with QM.

RECOMMENDATION:

Minimal, 0 Å, threshold maintains accuracy while significantly reducing computational time.

AIFDEM_CTSTATES

Include charge-transfer-like cation/anion pair states in the AIFDEM basis.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

TRUE

Include CT states.

FALSE

Do not include CT states.

RECOMMENDATION:

None

Example 13.338 Example showing singlet excited state calculation, on (H $_2$ O) $_4$ . XPol is used to generate monomer wave functions with ChElPG charges. Minimal QM charge embedding is used for the exciton model with three excited states per fragment.

$rem
   BASIS                aug-cc-pvdz
   EXCHANGE             HF
   CIS_N_ROOTS          3
   CIS_TRIPLETS         FALSE
   XPOL                 TRUE
   XPOL_CHARGE_TYPE     QCHELPG
   AIFDEM               TRUE
   AIFDEM_EMBED_RANGE   0
   AIFDEM_NTOTHRESH     90
   NTO_PAIRS            1
$end

$molecule
0 1
--H2O 0
   0 1
   O          1.74078        1.59716       -1.49814
   H          2.22908        2.18316       -2.08914
   H          0.88038        2.04726       -1.32684
--H2O 1
   0 1
   O          1.31998       -1.18934       -1.91734
   H          1.49988       -0.22974       -1.89044
   H          1.69058       -1.52594       -1.07704
--H2O 2
   0 1
   O         -0.68982        2.59476       -0.72224
   H         -1.14372        3.37086       -1.07364
   H         -1.35592        1.84986       -0.78334
--H2O 3
   0 1
   O         -1.27512       -1.77394       -1.69524
   H         -0.32252       -1.52884       -1.85604
   H         -1.53992       -2.30454       -2.45644
$end

13.15.3 Derivative Couplings

There are many chemical processes of interest where motion of nuclei induces electronic transitions, in a breakdown of the Born-Oppenheimer approximation. In order to investigate such processes it is useful to calculate some quantity that codifies the coupling of adiabatic electronic states dues to nuclear motion. In molecular electronic structure theory this quantity is the nonadiabatic coupling (or “derivative coupling”) vector $\langle \Psi _ I| (\partial /\partial x) | \Psi _ J\rangle$ , which describes how the nuclear position derivative $\partial /\partial x$ couples adiabatic (Born-Oppenheimer) electronic states $\Psi _ I$ and $\Psi _ J$ . In solid-state physics these ideas are typically not discussed in terms of the Born-Oppenheimer approximation but rather in terms of the so-called “Holstein” and “Peierls” exciton/phonon coupling constants (see below). Within the framework of the AIFDEM, each of these quantities can be computed from a common intermediate $\mathbf{H}^{[x]}$ , which is the derivative of the AIFDEM Hamiltonian matrix with respect to some nuclear coordinate $x$ .[Morrison and Herbert(2017a), Morrison and Herbert(2017b)] Diagonal matrix elements $H_{AA}^{[x]} \equiv \partial H_{AA}/\partial x$ describe how the exciton-site energies are modulated by nuclear motion and off-diagonal matrix elements $H_{AB}^{[x]} \equiv \partial H_{AB}/\partial x$ describe how nuclear motion modifies the energy-transfer couplings.

Once $\mathbf{H}^{[x]}$ has been constructed, then the nonadiabatic coupling vector between eigenstates $\Psi _ I$ and $\Psi _ J$ of the exciton Hamiltonian is simply

$\begin{equation} \mathbf{h}^{IJ}=\mathbf{K}_ I^\dagger \mathbf{H}^{[x]}\mathbf{K}_ J \; . \end{equation}$

(13.46)

The Holstein ( $A=B$ ) and Peierls ( $A\neq B$ ) coupling constants $g^{}_{AB\theta }$ , expressed in dimensionless normal mode coordinates, are[Morrison and Herbert(2017b)]

$\begin{equation} \label{eq:aifdem_ hols_ peierls} g^{}_{AB\theta } = \left(2\mu _{\theta }\omega _\theta \right) ^{-1/2} \sum _ x \widetilde{H}_{AB}^{[x]} L_{x\theta } \end{equation}$

(13.47)

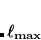where the matrix $\mathbf{L}$ is the transformation between Cartesians coordinates and normal (phonon) modes. The columns of $\mathbf{L}$ contain the normalized Cartesian displacements of normal mode $\theta$ , whose frequency and effective mass are $\omega _\theta$ and $\mu _\theta$ , respectively. The tilde on, $\widetilde{H}_{AB}^{[x]}$ indicates that the matrix element derivatives have been orthogonalized (including the derivative of the orthogonalization transformation).[Morrison and Herbert(2017b)]

13.15.4 Job Control for AIFDEM Derivative Couplings

Analytic evaluation of $\mathbf{H}^{[x]}$ and the analogous overlap derivative $\mathbf{S}^{[x]}$ have been implemented in Q-Chem.[Morrison and Herbert(2017b)] To compute AIFDEM derivatives, request a standard AIFDEM job and set CIS_STATE_DERIV = 1. Currently, the AIFDEM derivatives do not support charge embedding so the keyword AIFDEM_EMBED_RANGE must be omitted from these jobs; this precludes the use of XPol wavefunctions for the fragments. Furthermore, only one excited state per fragment is supported so the keyword CIS_N_ROOTS = 1. is required.

The derivatives of the AIFDEM Hamiltonian matrix and overlap matrix are printed in the output file in sets of the three Cartesian coordinates that belong to a single atom. For convenience, the orthogonalized AIFDEM Hamiltonian matrix elements are saved in the scratch directory, $QCSCRATCH/aifdem_deriv. These are organized such that the derivatives for each unique matrix element are stored in individual files in the order of the atomic Cartesian coordinates. These files can facilitate external calculation of exciton/phonon coupling constants.

Example 13.339

A basic AIFDEM derivative calculation on a chain of helium atoms.

$rem
basis = cc-pvdz
exchange = hf
aifdem = true
cis_n_roots = 1
cis_singlets = true
cis_triplets = false
cis_state_deriv = 1
nto_pairs = 1
mem_total = 1000
mem_static = 1000
max_cis_cycles = 200
max_scf_cycles = 200
thresh = 10
aifdem_ntothresh = 100
$end

$molecule
0 1
--frgm 0
0 1
He 0.0 0.0 0.0
He 0.0 0.0 1.4
--frgm 1
0 1
He 0.0 0.0 2.8
He 0.0 0.0 4.2
$end

FALSE	Do not perform an AIFDEM calculation.
TRUE	Perform an AIFDEM calculation.

FULL_QM	No charge embedding.
0	Treat only excited fragments with QM.
$n$	Range (Å) from excited fragments within which to treat other fragments with QM.