7.12 Visualization of Excited States
As methods for ab initio calculations of excited states are becoming increasingly more routine, questions arise concerning how best to extract chemical meaning from such calculations. There are several approaches for analyzing molecular excited states; they are based on reduced one-particle density matrices (OPDMs). The two objects exploited in this analysis are: (i) the difference between the ground- and excited-state OPDMs and (ii) the transition OPDM connecting the ground and excited state. In the case of CIS and TDDFT/TDA wave functions, both quantities are identical and can be directly mapped into the CIS amplitudes; however, for correlated wave functions the two objects are not the same. The most basic analysis includes calculation of attachment/detachment density[Head-Gordon et al.(1995a)Head-Gordon, Graña, Maurice, and White] and natural transition orbitals.[Martin(2003)] These quantities allow one to arrive to a most compact description of an excited state. More detailed analysis allows one to derive additional insight about the nature of the excited state. Detailed description and illustrative examples can be found in Refs. Plasser:2014a,Plasser:2014b.
This section describes the theoretical background behind attachment/detachment analysis and natural transition orbitals, while details of the input for creating data suitable for plotting these quantities is described separately in Chapter 11, which also describes additional excited-state analysis tools. For historical reasons, there are duplicate implementations of some features. For example, CIS and TDDFT wave functions can be analyzed using an original built-in code and by using a more recent module, libwfa.
7.12.1 Attachment/Detachment Density Analysis
Consider the one-particle density matrices of the initial and final states of interest,  and
and  respectively. Assuming that each state is represented in a finite basis of spin-orbitals, such as the molecular orbital basis, and each state is at the same geometry. Subtracting these matrices yields the difference density
respectively. Assuming that each state is represented in a finite basis of spin-orbitals, such as the molecular orbital basis, and each state is at the same geometry. Subtracting these matrices yields the difference density
 |
(7.97) |
Now, the eigenvectors of the one-particle density matrix 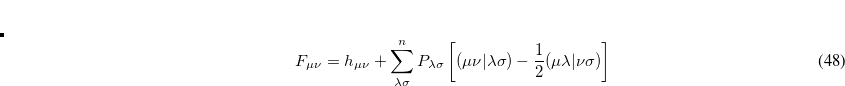 describing a single state are termed the natural orbitals, and provide the best orbital description that is possible for the state, in that a CI expansion using the natural orbitals as the single-particle basis is the most compact. The basis of the attachment/detachment analysis is to consider what could be termed natural orbitals of the electronic transition and their occupation numbers (associated eigenvalues). These are defined as the eigenvectors
describing a single state are termed the natural orbitals, and provide the best orbital description that is possible for the state, in that a CI expansion using the natural orbitals as the single-particle basis is the most compact. The basis of the attachment/detachment analysis is to consider what could be termed natural orbitals of the electronic transition and their occupation numbers (associated eigenvalues). These are defined as the eigenvectors  defined by
defined by
 |
(7.98) |
The sum of the occupation numbers  of these orbitals is then
of these orbitals is then
 |
(7.99) |
where  is the net gain or loss of electrons in the transition. The net gain in an electronic transition which does not involve ionization or electron attachment will obviously be zero.
is the net gain or loss of electrons in the transition. The net gain in an electronic transition which does not involve ionization or electron attachment will obviously be zero.
The detachment density
 |
(7.100) |
is defined as the sum of all natural orbitals of the difference density with negative occupation numbers, weighted by the absolute value of their occupations where  is a diagonal matrix with elements
is a diagonal matrix with elements
 |
(7.101) |
The detachment density corresponds to the electron density associated with single particle levels vacated in an electronic transition or hole density.
The attachment density
 |
(7.102) |
is defined as the sum of all natural orbitals of the difference density with positive occupation numbers where  is a diagonal matrix with elements
is a diagonal matrix with elements
 |
(7.103) |
The attachment density corresponds to the electron density associated with the single particle levels occupied in the transition or particle density. The difference between the attachment and detachment densities yields the original difference density matrix
 |
(7.104) |
7.12.2 Natural Transition Orbitals
In certain situations, even the attachment/detachment densities may be difficult to analyze. An important class of examples are systems with multiple chromophores, which may support exciton states consisting of linear combinations of localized excitations. For such states, both the attachment and the detachment density are highly delocalized and occupy basically the same region of space.[Lange and Herbert(2009)] Lack of phase information makes the attachment/detachment densities difficult to analyze, while strong mixing of the canonical MOs means that excitonic states are also difficult to characterize in terms of MOs.
Analysis of these and other excited states is greatly simplified by constructing Natural Transition Orbitals (NTOs) for the excited states. (The basic idea behind NTOs is rather old[Luzanov et al.(1976)Luzanov, Sukhorukov, and Umanskii] and has been rediscovered several times;[Martin(2003), Mayer(2007)] these orbitals were later shown to be equivalent to CIS natural orbitals.[Surján(2007)]) Let  denote the transition density matrix from an excited-state calculation. The dimension of this matrix is
denote the transition density matrix from an excited-state calculation. The dimension of this matrix is  , where
, where 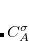 and
and 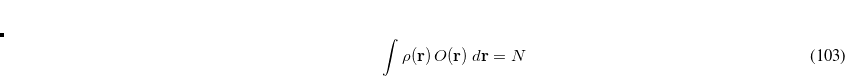 denote the number of occupied and virtual MOs, respectively. The NTOs are defined by transformations
denote the number of occupied and virtual MOs, respectively. The NTOs are defined by transformations  and
and  obtained by singular value decomposition (SVD) of the matrix
obtained by singular value decomposition (SVD) of the matrix  , i.e.,[Mayer(2007)]
, i.e.,[Mayer(2007)]
 |
(7.105) |
The matrices  and
and  are unitary and
are unitary and  is diagonal, with the latter containing at most
is diagonal, with the latter containing at most 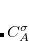 non-zero elements. The matrix
non-zero elements. The matrix  is a unitary transformation from the canonical occupied MOs to a set of NTOs that together represent the “hole” orbital that is left by the excited electron, while
is a unitary transformation from the canonical occupied MOs to a set of NTOs that together represent the “hole” orbital that is left by the excited electron, while  transforms the canonical virtual MOs into a set of NTOs representing the excited electron. (Equivalently, the “holes” are the eigenvectors of the
transforms the canonical virtual MOs into a set of NTOs representing the excited electron. (Equivalently, the “holes” are the eigenvectors of the  matrix
matrix  and the particles are eigenvectors of the
and the particles are eigenvectors of the  matrix
matrix  .[Martin(2003)]) These “hole” and “particle” NTOs come in pairs, and their relative importance in describing the excitation is governed by the diagonal elements of
.[Martin(2003)]) These “hole” and “particle” NTOs come in pairs, and their relative importance in describing the excitation is governed by the diagonal elements of  , which are excitation amplitudes in the NTO basis. By virtue of the SVD in Eq. eq:NTO_SVD, any excited state may be represented using at most
, which are excitation amplitudes in the NTO basis. By virtue of the SVD in Eq. eq:NTO_SVD, any excited state may be represented using at most 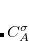 excitation amplitudes and corresponding hole/particle NTO pairs. (The‘ discussion here assumes that
excitation amplitudes and corresponding hole/particle NTO pairs. (The‘ discussion here assumes that  , which is typically the case except possibly in minimal basis sets. Although it is possible to use the transpose of Eq. eq:NTO_SVD to obtain NTOs when
, which is typically the case except possibly in minimal basis sets. Although it is possible to use the transpose of Eq. eq:NTO_SVD to obtain NTOs when  , this has not been implemented in Q-Chem due to its limited domain of applicability.)
, this has not been implemented in Q-Chem due to its limited domain of applicability.)
The SVD generalizes the concept of matrix diagonalization to the case of rectangular matrices, and therefore reduces as much as possible the number of non-zero outer products needed for an exact representation of  . In this sense, the NTOs represent the best possible particle/hole picture of an excited state. The detachment density is recovered as the sum of the squares of the “hole” NTOs, while the attachment density is precisely the sum of the squares of the “particle” NTOs. Unlike the attachment/detachment densities, however, NTOs preserve phase information, which can be very helpful in characterizing the diabatic character (e.g.,
. In this sense, the NTOs represent the best possible particle/hole picture of an excited state. The detachment density is recovered as the sum of the squares of the “hole” NTOs, while the attachment density is precisely the sum of the squares of the “particle” NTOs. Unlike the attachment/detachment densities, however, NTOs preserve phase information, which can be very helpful in characterizing the diabatic character (e.g.,  or
or  ) of excited states in complex systems. Even when there is more than one significant NTO amplitude, as in systems of electronically-coupled chromophores,[Lange and Herbert(2009)] the NTOs still represent a significant compression of information, as compared to the canonical MO basis.
) of excited states in complex systems. Even when there is more than one significant NTO amplitude, as in systems of electronically-coupled chromophores,[Lange and Herbert(2009)] the NTOs still represent a significant compression of information, as compared to the canonical MO basis.
NTOs are available within Q-Chem for CIS, RPA, TDDFT, ADC, and EOM-CC methods. For the correlated wave functions (EOM-CC and ADC), they can be computed using libwfa module. The simplest way to visualize the NTOs is to generate them in a format suitable for viewing with the freely-available MolDen or MacMolPlt programs, as described in Chapter 11.