Q-Chem 4.3 User’s Manual

4.2 Hartree–Fock Calculations

4.2.1 The Hartree-Fock Equations

As with much of the theory underlying modern quantum chemistry, the Hartree-Fock approximation was developed shortly after publication of the Schrödinger equation, but remained a qualitative theory until the advent of the computer. Although the HF approximation tends to yield qualitative chemical accuracy, rather than quantitative information, and is generally inferior to many of the DFT approaches available, it remains as a useful tool in the quantum chemist’s toolkit. In particular, for organic chemistry, HF predictions of molecular structure are very useful.

Consider once more the Roothaan-Hall equations, Eq. (4.11), or the Pople-Nesbet equations, Eq. (4.13), which can be traced back to the integro–differential Eq. (4.8) in which the effective potential 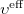$\upsilon ^{\mathrm{eff}}$ depends on the SCF methodology. In a restricted HF (RHF) formalism, the effective potential can be written as

  \begin{equation} \label{eq413} \upsilon ^{\mathrm{eff}}=\sum \limits _{a}^{N/2} {\left[ {2J_ a (1)-K_ a (1)} \right]} -\sum \limits _{A=1}^ M {\frac{Z_ A }{r_{1A} }} \end{equation}   (4.14)

where the Coulomb and exchange operators are defined as

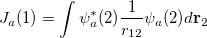  \begin{equation} \label{eq414} J_ a (1)=\int {\psi _ a^\ast (2)\frac{1}{r_{12} }\psi _ a (2)d{\rm {\bf r}}_{ 2} } \end{equation}   (4.15)

and

  \begin{equation} \label{eq415} K_ a (1)\psi _ i (1)=\left[ {\int {\psi _ a^\ast (2)\frac{1}{r_{12} }\psi _ i (2)d{\rm {\bf r}}_{ 2} } } \right]\psi _ a (1) \end{equation}   (4.16)

respectively. By introducing an atomic orbital basis, we obtain Fock matrix elements

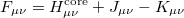  \begin{equation} \label{eq416} F_{\mu \nu } =H_{\mu \nu }^{\mathrm{core}} +J_{\mu \nu } -K_{\mu \nu } \end{equation}   (4.17)

where the core Hamiltonian matrix elements

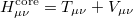  \begin{equation} \label{eq417} H_{\mu \nu }^{\mathrm{core}} =T_{\mu \nu } +V_{\mu \nu } \end{equation}   (4.18)

consist of kinetic energy elements

  \begin{equation} \label{eq418} T_{\mu \nu } =\int {\phi _\mu ({\rm {\bf r}})\left[ {-\frac{1}{2}\nabla ^2} \right]\phi _\nu ({\rm {\bf r}})d{\rm {\bf r}}} \end{equation}   (4.19)

and nuclear attraction elements

  \begin{equation} \label{eq419} V_{\mu \nu } =\int {\phi _\mu ({\rm {\bf r}})\left[ {-\sum \limits _ A {\frac{Z_ A }{\left| {{\rm {\bf R}}_{ A} -{\rm {\bf r}}} \right|}} } \right]\phi _\nu ({\rm {\bf r}})d{\rm {\bf r}}} \end{equation}   (4.20)

The Coulomb and Exchange elements are given by

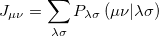  \begin{equation} \label{eq420} J_{\mu \nu } =\sum \limits _{\lambda \sigma } {P_{\lambda \sigma } \left( {\mu \nu \vert \lambda \sigma } \right)} \end{equation}   (4.21)

and

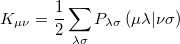  \begin{equation} \label{eq421} K_{\mu \nu } =\frac{1}{2}\sum \limits _{\lambda \sigma } {P_{\lambda \sigma } \left( {\mu \lambda \vert \nu \sigma } \right)} \end{equation}   (4.22)

respectively, where the density matrix elements are

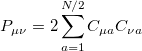  \begin{equation} \label{eq422} P_{\mu \nu } =2\sum \limits _{a=1}^{N/2} {C_{\mu a} C_{\nu a} } \end{equation}   (4.23)

and the two electron integrals are

  \begin{equation} \label{eq423} \left( {\mu \nu \vert \lambda \sigma } \right)= \int \int {\phi _\mu ({\rm {\bf r}}_{ 1} )\phi _\nu ({\rm {\bf r}}_{ 1} )\left[ {\frac{1}{r_{12} }} \right]\phi _\lambda ({\rm {\bf r}}_{ 2} )\phi _\sigma ({\rm {\bf r}}_{\rm {\bf 2}} )d{\rm {\bf r}}_{ 1} d{\rm {\bf r}}_{ 2} } \end{equation}   (4.24)

Note: The formation and utilization of two-electron integrals is a topic central to the overall performance of SCF methodologies. The performance of the SCF methods in new quantum chemistry software programs can be quickly estimated simply by considering the quality of their atomic orbital integrals packages. See Appendix B for details of Q-Chem’s AOINTS package.

Substituting the matrix element in Eq. (4.17) back into the Roothaan-Hall equations, Eq. (4.11), and iterating until self-consistency is achieved will yield the Restricted Hartree-Fock (RHF) energy and wavefunction. Alternatively, one could have adopted the unrestricted form of the wavefunction by defining an alpha and beta density matrix:

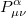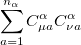  $\displaystyle \label{eq424} P_{\mu \nu }^{\alpha } $ $\displaystyle = $ $\displaystyle \sum \limits _{a=1}^{n_\alpha } {C_{\mu a}^\alpha C_{\nu a}^\alpha } \nonumber $    
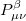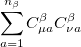  $\displaystyle P_{\mu \nu }^{\beta } $ $\displaystyle = $ $\displaystyle \sum \limits _{a=1}^{n_\beta } {C_{\mu a}^\beta C_{\nu a}^\beta } $   (4.25)

The total electron density matrix 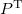$P^{\mathrm{T}}$ is simply the sum of the alpha and beta density matrices. The unrestricted alpha Fock matrix,

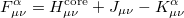  \begin{equation} \label{eq425} F_{\mu \nu }^\alpha =H_{\mu \nu }^{\mathrm{core}} +J_{\mu \nu } -K_{\mu \nu }^\alpha \end{equation}   (4.26)

differs from the restricted one only in the exchange contributions where the alpha exchange matrix elements are given by

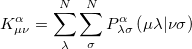  \begin{equation} \label{eq426} K_{\mu \nu }^\alpha =\sum \limits _\lambda ^ N {\sum \limits _\sigma ^ N {P_{\lambda \sigma }^\alpha \left( {\mu \lambda \vert \nu \sigma } \right)} } \end{equation}   (4.27)

4.2.2 Wavefunction Stability Analysis

At convergence, the SCF energy will be at a stationary point with respect to changes in the MO coefficients. However, this stationary point is not guaranteed to be an energy minimum, and in cases where it is not, the wavefunction is said to be unstable. Even if the wavefunction is at a minimum, this minimum may be an artifact of the constraints placed on the form of the wavefunction. For example, an unrestricted calculation will usually give a lower energy than the corresponding restricted calculation, and this can give rise to a RHF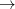$\to $UHF instability.

To understand what instabilities can occur, it is useful to consider the most general form possible for the spin orbitals:

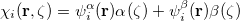  \begin{equation} \label{eq427} \chi _ i ({\rm {\bf r}},\zeta )=\psi _ i^\alpha ({\rm {\bf r}})\alpha (\zeta )+\psi _ i^\beta ({\rm {\bf r}})\beta (\zeta ) \end{equation}   (4.28)

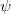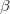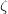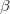Here, the $\psi $’s are complex functions of the Cartesian coordinates $\ensuremath{\mathbf{r}}$, and $\alpha $ and $\beta $ are spin eigenfunctions of the spin-variable $\zeta $. The first constraint that is almost universally applied is to assume the spin orbitals depend only on one or other of the spin-functions $\alpha $ or $\beta $. Thus, the spin-functions take the form

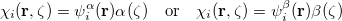  \begin{equation} \chi _ i(\ensuremath{\mathbf{r}},\zeta )=\psi _ i^\alpha (\ensuremath{\mathbf{r}})\alpha (\zeta ) \quad \mathrm{or} \quad \chi _ i(\ensuremath{\mathbf{r}},\zeta )=\psi _ i^\beta (\ensuremath{\mathbf{r}})\beta (\zeta ) \end{equation}   (4.29)

where the 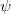$\psi $’s are still complex functions. Most SCF packages, including Q-Chem’s, deal only with real functions, and this places an additional constraint on the form of the wavefunction. If there exists a complex solution to the SCF equations that has a lower energy, the wavefunction will exhibit either a RHF 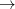$\to $ CRHF or a UHF 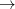$\to $ CUHF instability. The final constraint that is commonly placed on the spin-functions is that 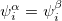$\psi _ i^\alpha =\psi _ i^\beta $, i.e., the spatial parts of the spin-up and spin-down orbitals are the same. This gives the familiar restricted formalism and can lead to a RHF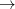$\to $UHF instability as mentioned above. Further details about the possible instabilities can be found in Ref. Seeger:1977.

Wavefunction instabilities can arise for several reasons, but frequently occur if

If a wavefunction exhibits an instability, the seriousness of it can be judged from the magnitude of the negative eigenvalues of the stability matrices. These matrices and eigenvalues are computed by Q-Chem’s Stability Analysis package, which was implemented by Dr Yihan Shao. The package is invoked by setting the STABILITY_ANALYSIS $rem variable is set to TRUE. In order to compute these stability matrices Q-Chem must first perform a CIS calculation. This will be performed automatically, and does not require any further input from the user. By default Q-Chem computes only the lowest eigenvalue of the stability matrix. This is usually sufficient to determine if there is a negative eigenvalue, and therefore an instability. Users wishing to calculate additional eigenvalues can do so by setting the CIS_N_ROOTS $rem variable to a number larger than 1.

Q-Chem’s Stability Analysis package also seeks to correct internal instabilities (RHF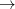$\to $RHF or UHF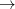$\to $UHF). Then, if such an instability is detected, Q-Chem automatically performs a unitary transformation of the molecular orbitals following the directions of the lowest eigenvector, and writes a new set of MOs to disk. One can read in these MOs as an initial guess in a second SCF calculation (set the SCF_GUESS $rem variable to READ), it might also be desirable to set the SCF_ALGORITHM to GDM. In cases where the lowest-energy SCF solution breaks the molecular point-group symmetry, the SYM_IGNORE $rem should be set to TRUE.

Note: The stability analysis package can be used to analyze both DFT and HF wavefunctions.

4.2.3 Basic Hartree-Fock Job Control

In brief, Q-Chem supports the three main variants of the Hartree-Fock method. They are:

Only two $rem variables are required in order to run Hartree-Fock (HF) calculations:

In slightly more detail, here is a list of basic $rem variables associated with running Hartree-Fock calculations. See Chapter 7 for further detail on basis sets available and Chapter 8 for specifying effective core potentials.

JOBTYPE

Specifies the type of calculation.


TYPE:

STRING


DEFAULT:

SP


OPTIONS:

SP

Single point energy.

OPT

Geometry Minimization.

TS

Transition Structure Search.

FREQ

Frequency Calculation.

FORCE

Analytical Force calculation.

RPATH

Intrinsic Reaction Coordinate calculation.

NMR

NMR chemical shift calculation.

ISSC

Indirect nuclear spin–spin coupling calculation.

BSSE

BSSE calculation.

EDA

Energy decomposition analysis.


RECOMMENDATION:

Job dependent


METHOD

Specifies the level of theory.


TYPE:

STRING


DEFAULT:

No default


OPTIONS:

HF

Exact (Hartree-Fock).


RECOMMENDATION:

Use HF for Hartree-Fock calculations.


BASIS

Specifies the basis sets to be used.


TYPE:

STRING


DEFAULT:

No default basis set


OPTIONS:

General, Gen

User defined ($basis keyword required).

Symbol

Use standard basis sets as per Chapter 7.

Mixed

Use a mixture of basis sets (see Chapter 7).


RECOMMENDATION:

Consult literature and reviews to aid your selection.


PRINT_ORBITALS

Prints orbital coefficients with atom labels in analysis part of output.


TYPE:

INTEGER/LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Do not print any orbitals.

TRUE

Prints occupied orbitals plus 5 virtuals.

NVIRT

Number of virtuals to print.


RECOMMENDATION:

Use TRUE unless more virtuals are desired.


THRESH

Cutoff for neglect of two electron integrals. $10^{-\mathrm{THRESH}}$ (THRESH $\le 14$).


TYPE:

INTEGER


DEFAULT:

8

For single point energies.

10

For optimizations and frequency calculations.

14

For coupled-cluster calculations.


OPTIONS:

$n$

for a threshold of $10^{-n}$.

RECOMMENDATION:

Should be at least three greater than SCF_CONVERGENCE. Increase for more significant figures, at greater computational cost.


SCF_CONVERGENCE

SCF is considered converged when the wavefunction error is less that $10^{-\mathrm{SCF\_ CONVERGENCE}}$. Adjust the value of THRESH at the same time. Note that in Q-Chem 3.0 the DIIS error is measured by the maximum error rather than the RMS error as in previous versions.


TYPE:

INTEGER


DEFAULT:

5

For single point energy calculations.

8

For geometry optimizations and vibrational analysis.

8

For SSG calculations, see Chapter 5.


OPTIONS:

User-defined


RECOMMENDATION:

Tighter criteria for geometry optimization and vibration analysis. Larger values provide more significant figures, at greater computational cost.


UNRESTRICTED

Controls the use of restricted or unrestricted orbitals.


TYPE:

LOGICAL


DEFAULT:

FALSE

(Restricted) Closed-shell systems.

TRUE

(Unrestricted) Open-shell systems.


OPTIONS:

TRUE

(Unrestricted) Open-shell systems.

FALSE

Restricted open-shell HF (ROHF).


RECOMMENDATION:

Use default unless ROHF is desired. Note that for unrestricted calculations on systems with an even number of electrons it is usually necessary to break alpha/beta symmetry in the initial guess, by using SCF_GUESS_MIX or providing $occupied information (see Section 4.4 on initial guesses).


4.2.4 Additional Hartree-Fock Job Control Options

Listed below are a number of useful options to customize a Hartree-Fock calculation. This is only a short summary of the function of these $rem variables. A full list of all SCF-related variables is provided in Appendix C. A number of other specialized topics (large molecules, customizing initial guesses, and converging the calculation) are discussed separately in Sections 4.6, 4.4, and 4.5, respectively.

INTEGRALS_BUFFER

Controls the size of in-core integral storage buffer.


TYPE:

INTEGER


DEFAULT:

15

15 Megabytes.


OPTIONS:

User defined size.


RECOMMENDATION:

Use the default, or consult your systems administrator for hardware limits.


DIRECT_SCF

Controls direct SCF.


TYPE:

LOGICAL


DEFAULT:

Determined by program.


OPTIONS:

TRUE

Forces direct SCF.

FALSE

Do not use direct SCF.


RECOMMENDATION:

Use default; direct SCF switches off in-core integrals.


METECO

Sets the threshold criteria for discarding shell-pairs.


TYPE:

INTEGER


DEFAULT:

2

Discard shell-pairs below $10^{-\mathrm{THRESH}}$.


OPTIONS:

1

Discard shell-pairs four orders of magnitude below machine precision.

2

Discard shell-pairs below 10$^{-\mathrm{THRESH}}$.


RECOMMENDATION:

Use default.


STABILITY_ANALYSIS

Performs stability analysis for a HF or DFT solution.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

TRUE

Perform stability analysis.

FALSE

Do not perform stability analysis.


RECOMMENDATION:

Set to TRUE when a HF or DFT solution is suspected to be unstable.


SCF_PRINT

Controls level of output from SCF procedure to Q-Chem output file.


TYPE:

INTEGER


DEFAULT:

0

Minimal, concise, useful and necessary output.


OPTIONS:

0

Minimal, concise, useful and necessary output.

1

Level 0 plus component breakdown of SCF electronic energy.

2

Level 1 plus density, Fock and MO matrices on each cycle.

3

Level 2 plus two-electron Fock matrix components (Coulomb, HF exchange

 

and DFT exchange-correlation matrices) on each cycle.


RECOMMENDATION:

Proceed with care; can result in extremely large output files at level 2 or higher. These levels are primarily for program debugging.


SCF_FINAL_PRINT

Controls level of output from SCF procedure to Q-Chem output file at the end of the SCF.


TYPE:

INTEGER


DEFAULT:

0

No extra print out.


OPTIONS:

0

No extra print out.

1

Orbital energies and break-down of SCF energy.

2

Level 1 plus MOs and density matrices.

3

Level 2 plus Fock and density matrices.


RECOMMENDATION:

The break-down of energies is often useful (level 1).


KS_GAP_PRINT

Control printing of (generalized Kohn-Sham) HOMO-LUMO gap information.


TYPE:

Boolean


DEFAULT:

false


OPTIONS:

false

(default) do not print gap information

true

print gap information


RECOMMENDATION:

Use in conjunction with KS_GAP_UNIT if true.


KS_GAP_UNIT

Unit for KS_GAP_PRINT and FOA_FUNDGAP


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

(default) hartrees

1

eV


RECOMMENDATION:

none


DIIS_SEPARATE_ERRVEC

Control optimization of DIIS error vector in unrestricted calculations.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use a combined alpha and beta error vector.


OPTIONS:

FALSE

Use a combined alpha and beta error vector.

TRUE

Use separate error vectors for the alpha and beta spaces.


RECOMMENDATION:

When using DIIS in Q-Chem a convenient optimization for unrestricted calculations is to sum the alpha and beta error vectors into a single vector which is used for extrapolation. This is often extremely effective, but in some pathological systems with symmetry breaking, can lead to false solutions being detected, where the alpha and beta components of the error vector cancel exactly giving a zero DIIS error. While an extremely uncommon occurrence, if it is suspected, set DIIS_SEPARATE_ERRVEC to TRUE to check.


4.2.5 Examples

Provided below are examples of Q-Chem input files to run ground state, Hartree-Fock single point energy calculations.

Example 4.19  Example Q-Chem input for a single point energy calculation on water. Note that the declaration of the single point $rem variable and level of theory to treat correlation are redundant because they are the same as the Q-Chem defaults.

$molecule
   0  1
   O
   H1  O  oh
   H2  O  oh  H1  hoh

   oh  =   1.2
   hoh = 120.0
$end

$rem
   JOBTYPE       sp       Single Point energy
   METHOD        hf       Hartree-Fock
   BASIS         sto-3g   Basis set
$end

$comment
HF/STO-3G water single point calculation
$end

Example 4.20  UHF/6-311G calculation on the Lithium atom. Note that correlation and the job type were not indicated because Q-Chem defaults automatically to no correlation and single point energies. Note also that, since the number of alpha and beta electron differ, MOs default to an unrestricted formalism.

$molecule
   0,2
   3
$end

$rem
   METHOD     HF       Hartree-Fock
   BASIS      6-311G   Basis set
$end

Example 4.21  ROHF/6-311G calculation on the Lithium atom. Note again that correlation and the job type need not be indicated.

$molecule
   0,2
   3
$end

$rem
   METHOD         hf       Hartree-Fock
   UNRESTRICTED   false    Restricted MOs
   BASIS          6-311G   Basis set
$end

Example 4.22  RHF/6-31G stability analysis calculation on the singlet state of the oxygen molecule. The wavefunction is RHF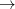$\to $UHF unstable.

$molecule
   0 1
   O
   O  1  1.165
$end

$rem
   METHOD               hf         Hartree-Fock
   UNRESTRICTED         false      Restricted MOs
   BASIS                6-31G(d)   Basis set
   STABILITY_ANALYSIS   true       Perform a stability analysis
$end

4.2.6 Symmetry

Symmetry is a powerful branch of mathematics and is often exploited in quantum chemistry, both to reduce the computational workload and to classify the final results obtained [18, 19, 20]. Q-Chem is able to determine the point group symmetry of the molecular nuclei and, on completion of the SCF procedure, classify the symmetry of molecular orbitals, and provide symmetry decomposition of kinetic and nuclear attraction energy (see Chapter 10).

Molecular systems possessing point group symmetry offer the possibility of large savings of computational time, by avoiding calculations of integrals which are equivalent i.e., those integrals which can be mapped on to one another under one of the symmetry operations of the molecular point group. The Q-Chem default is to use symmetry to reduce computational time, when possible.

There are several keywords that are related to symmetry, which causes frequent confusion. SYM_IGNORE controls symmetry throughout all modules. The default is FALSE. In some cases it may be desirable to turn off symmetry altogether, for example if you do not want Q-Chem to reorient the molecule into the standard nuclear orientation, or if you want to turn it off for finite difference calculations. If the SYM_IGNORE $rem is set to TRUE then the coordinates will not be altered from the input, and the point group will be set to 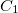$C_1$.

The SYMMETRY (an alias for ISYM_RQ) keyword controls symmetry in some integral routines. It is set to FALSE by default. Note that setting it to FALSE does not turn point group symmetry off, and does not disable symmetry in the coupled-cluster suite (CCMAN and CCMAN2), which is controlled by CC_SYMMETRY (see Chapters 5 and 6), although we noticed that sometimes it may mess up the determination of orbital symmetries, possibly due to numeric noise. In some cases, SYMMETRY=TRUE can cause problems (poor convergence and crazy SCF energies) and turning it off can help.

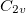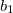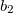Note: The user should be aware about different conventions for defining symmetry elements. The arbitrariness affects, for example, $C_{2v}$ point group. The specific choice affects how the irreps in the affected groups are labeled. For example, $b_1$ and $b_2$ irreps in 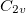$C_{2v}$ are flipped when using different conventions. Q-Chem uses non-Mulliken symmetry convention. See http://iopenshell.usc.edu/howto/symmetry for detailed explanations.

SYMMETRY

Controls the efficiency through the use of point group symmetry for calculating integrals.


TYPE:

LOGICAL


DEFAULT:

TRUE

Use symmetry for computing integrals.


OPTIONS:

TRUE

Use symmetry when available.

FALSE

Do not use symmetry. This is always the case for RIMP2 jobs


RECOMMENDATION:

Use default unless benchmarking. Note that symmetry usage is disabled for RIMP2, FFT, and QM/MM jobs.


SYM_IGNORE

Controls whether or not Q-Chem determines the point group of the molecule and reorients the molecule to the standard orientation.


TYPE:

LOGICAL


DEFAULT:

FALSE

Do determine the point group (disabled for RIMP2 jobs).


OPTIONS:

TRUE/FALSE


RECOMMENDATION:

Use default unless you do not want the molecule to be reoriented. Note that symmetry usage is disabled for RIMP2 jobs.


SYM_TOL

Controls the tolerance for determining point group symmetry. Differences in atom locations less than $10^{-\mathrm{SYM\_ TOL}}$ are treated as zero.


TYPE:

INTEGER


DEFAULT:

5

corresponding to $10^{-5}$.


OPTIONS:

User defined.


RECOMMENDATION:

Use the default unless the molecule has high symmetry which is not being correctly identified. Note that relaxing this tolerance too much may introduce errors into the calculation.