Q-Chem 4.3 User’s Manual

4.5 Converging SCF Calculations

4.5.1 Introduction

As for any numerical optimization procedure, the rate of convergence of the SCF procedure is dependent on the initial guess and on the algorithm used to step towards the stationary point. Q-Chem features a number of alternative SCF optimization algorithms, which are discussed in the following sections, along with the $rem variables that are used to control the calculations. The main options are discussed in sections which follow and are, in brief:

4.5.2 Basic Convergence Control Options

See also more detailed options in the following sections, and note that the SCF convergence criterion and the integral threshold must be set in a compatible manner, (this usually means THRESH should be set to at least 3 higher than SCF_CONVERGENCE).

MAX_SCF_CYCLES

Controls the maximum number of SCF iterations permitted.


TYPE:

INTEGER


DEFAULT:

50


OPTIONS:

User-defined.


RECOMMENDATION:

Increase for slowly converging systems such as those containing transition metals.


SCF_ALGORITHM

Algorithm used for converging the SCF.


TYPE:

STRING


DEFAULT:

DIIS

Pulay DIIS.


OPTIONS:

DIIS

Pulay DIIS.

DM

Direct minimizer.

DIIS_DM

Uses DIIS initially, switching to direct minimizer for later iterations

 

(See THRESH_DIIS_SWITCH, MAX_DIIS_CYCLES).

DIIS_GDM

Use DIIS and then later switch to geometric direct minimization

 

(See THRESH_DIIS_SWITCH, MAX_DIIS_CYCLES).

GDM

Geometric Direct Minimization.

RCA

Relaxed constraint algorithm

RCA_DIIS

Use RCA initially, switching to DIIS for later iterations (see
 

THRESH_RCA_SWITCH and MAX_RCA_CYCLES described

 

later in this chapter)

ROOTHAAN

Roothaan repeated diagonalization.


RECOMMENDATION:

Use DIIS unless performing a restricted open-shell calculation, in which case GDM is recommended. If DIIS fails to find a reasonable approximate solution in the initial iterations, RCA_DIIS is the recommended fallback option. If DIIS approaches the correct solution but fails to finally converge, DIIS_GDM is the recommended fallback.


SCF_CONVERGENCE

SCF is considered converged when the wavefunction error is less that $10^{-\mathrm{SCF\_ CONVERGENCE}}$. Adjust the value of THRESH at the same time. Note that in Q-Chem 3.0 the DIIS error is measured by the maximum error rather than the RMS error.


TYPE:

INTEGER


DEFAULT:

5

For single point energy calculations.

7

For geometry optimizations and vibrational analysis.

8

For SSG calculations, see Chapter 5.


OPTIONS:

$n$

Corresponding to $10^{-n}$


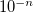
RECOMMENDATION:

Tighter criteria for geometry optimization and vibration analysis. Larger values provide more significant figures, at greater computational cost.


In some cases besides the total SCF energy, one needs its separate energy components, like kinetic energy, exchange energy, correlation energy, etc. The values of these components are printed at each SCF cycle if one specifies in the input: SCF_PRINT 1 .

4.5.3 Direct Inversion in the Iterative Subspace (DIIS)

The SCF implementation of the Direct Inversion in the Iterative Subspace (DIIS) method [163, 164] uses the property of an SCF solution that requires the density matrix to commute with the Fock matrix:

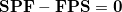  \begin{equation} \label{eq445} {\rm {\bf SPF}}-{\rm {\bf FPS}}={\rm {\bf 0}} \end{equation}   (4.75)

During the SCF cycles, prior to achieving self-consistency, it is therefore possible to define an error vector e$_{i}$, which is non-zero except at convergence:

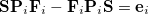  \begin{equation} \label{eq446} {\rm {\bf SP}}_ i {\rm {\bf F}}_ i -{\rm {\bf F}}_ i {\rm {\bf P}}_ i {\rm {\bf S}}={\rm {\bf e}}_ i \end{equation}   (4.76)

Here, P$_{i}$ is obtained from diagonalization of 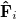${\rm {\bf \hat{F}}}_ i $, and

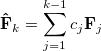  \begin{equation} \label{eq447} {\rm {\bf \hat{F}}}_ k =\sum \limits _{j=1}^{k-1} {c_ j {\rm {\bf F}}_ j } \end{equation}   (4.77)

The DIIS coefficients 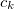$c_ k$, are obtained by a least-squares constrained minimization of the error vectors, viz

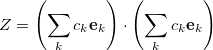  \begin{equation} \label{eq448} Z=\left( {\sum \limits _ k {c_ k {\rm {\bf e}}_ k } } \right)\cdot \left( {\sum \limits _ k {c_ k {\rm {\bf e}}_ k } } \right) \end{equation}   (4.78)

where the constraint

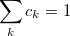  \begin{equation} \label{eq449} \sum \limits _ k {c_ k } =1 \end{equation}   (4.79)

is imposed to yield a set of linear equations, of dimension 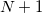$N+1$:

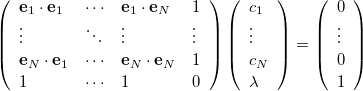  \begin{equation} \label{eq450} \left( {{\begin{array}{*{20}c} {{\rm {\bf e}}_1 \cdot {\rm {\bf e}}_1 } \hfill & \cdots \hfill & {{\rm {\bf e}}_1 \cdot {\rm {\bf e}}_ N } \hfill & 1 \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ {{\rm {\bf e}}_ N \cdot {\rm {\bf e}}_1 } \hfill & \cdots \hfill & {{\rm {\bf e}}_ N \cdot {\rm {\bf e}}_ N } \hfill & 1 \hfill \\ 1 \hfill & \cdots \hfill & 1 \hfill & 0 \hfill \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {c_1 } \hfill \\ \vdots \hfill \\ {c_ N } \hfill \\ \lambda \hfill \\ \end{array} }} \right)=\left( {{\begin{array}{*{20}c} 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{array} }} \right) \end{equation}   (4.80)

Convergence criteria requires the largest element of the 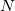$N$th error vector to be below a cutoff threshold, usually 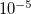$10^{-5}$ for single point energies, often increased to 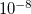$10^{-8}$ for optimizations and frequency calculations.

The rate of convergence may be improved by restricting the number of previous Fock matrices (size of the DIIS subspace, $rem variable DIIS_SUBSPACE_SIZE) used for determining the DIIS coefficients:

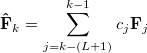  \begin{equation} \label{eq451} {\rm {\bf \hat{F}}}_ k =\sum \limits _{j=k-(L+1)}^{k-1} {c_ j {\rm {\bf F}}_ j } \end{equation}   (4.81)

where 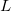$L$ is the size of the DIIS subspace. As the Fock matrix nears self-consistency, the linear matrix equations in Eq. (4.80) tend to become severely ill-conditioned and it is often necessary to reset the DIIS subspace (this is automatically carried out by the program).

Finally, on a practical note, we observe that DIIS has a tendency to converge to global minima rather than local minima when employed for SCF calculations. This seems to be because only at convergence is the density matrix in the DIIS iterations idempotent. On the way to convergence, one is not on the “true” energy surface, and this seems to permit DIIS to “tunnel” through barriers in wavefunction space. This is usually a desirable property, and is the motivation for the options that permit initial DIIS iterations before switching to direct minimization to converge to the minimum in difficult cases.

The following $rem variables permit some customization of the DIIS iterations:

DIIS_SUBSPACE_SIZE

Controls the size of the DIIS and/or RCA subspace during the SCF.


TYPE:

INTEGER


DEFAULT:

15


OPTIONS:

User-defined


RECOMMENDATION:

None


DIIS_PRINT

Controls the output from DIIS SCF optimization.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Minimal print out.

1

Chosen method and DIIS coefficients and solutions.

2

Level 1 plus changes in multipole moments.

3

Level 2 plus Multipole moments.

4

Level 3 plus extrapolated Fock matrices.


RECOMMENDATION:

Use default


Note: In Q-Chem 3.0 the DIIS error is determined by the maximum error rather than the RMS error. For backward compatibility the RMS error can be forced by using the following $rem

DIIS_ERR_RMS

Changes the DIIS convergence metric from the maximum to the RMS error.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

TRUE, FALSE


RECOMMENDATION:

Use default, the maximum error provides a more reliable criterion.


4.5.4 Geometric Direct Minimization (GDM)

Troy Van Voorhis, working at Berkeley with Martin Head-Gordon, has developed a novel direct minimization method that is extremely robust, and at the same time is only slightly less efficient than DIIS. This method is called geometric direct minimization (GDM) because it takes steps in an orbital rotation space that correspond properly to the hyper-spherical geometry of that space. In other words, rotations are variables that describe a space which is curved like a many-dimensional sphere. Just like the optimum flight paths for airplanes are not straight lines but great circles, so too are the optimum steps in orbital rotation space. GDM takes this correctly into account, which is the origin of its efficiency and its robustness. For full details, we refer the reader to Ref. VanVoorhis:2002a. GDM is a good alternative to DIIS for SCF jobs that exhibit convergence difficulties with DIIS.

Recently, Barry Dunietz, also working at Berkeley with Martin Head-Gordon, has extended the GDM approach to restricted open-shell SCF calculations. Their results indicate that GDM is much more efficient than the older direct minimization method (DM).

In section 4.5.3, we discussed the fact that DIIS can efficiently head towards the global SCF minimum in the early iterations. This can be true even if DIIS fails to converge in later iterations. For this reason, a hybrid scheme has been implemented which uses the DIIS minimization procedure to achieve convergence to an intermediate cutoff threshold. Thereafter, the geometric direct minimization algorithm is used. This scheme combines the strengths of the two methods quite nicely: the ability of DIIS to recover from initial guesses that may not be close to the global minimum, and the ability of GDM to robustly converge to a local minimum, even when the local surface topology is challenging for DIIS. This is the recommended procedure with which to invoke GDM (i.e., setting SCF_ALGORITHM = DIIS_GDM). This hybrid procedure is also compatible with the SAD guess, while GDM itself is not, because it requires an initial guess set of orbitals. If one wishes to disturb the initial guess as little as possible before switching on GDM, one should additionally specify MAX_DIIS_CYCLES = 1 to obtain only a single Roothaan step (which also serves up a properly orthogonalized set of orbitals).

$rem options relevant to GDM are SCF_ALGORITHM which should be set to either GDM or DIIS_GDM and the following:

MAX_DIIS_CYCLES

The maximum number of DIIS iterations before switching to (geometric) direct minimization when SCF_ALGORITHM is DIIS_GDM or DIIS_DM. See also THRESH_DIIS_SWITCH.


TYPE:

INTEGER


DEFAULT:

50


OPTIONS:

1

Only a single Roothaan step before switching to (G)DM

$n$

$n$ DIIS iterations before switching to (G)DM.


RECOMMENDATION:

None


THRESH_DIIS_SWITCH

The threshold for switching between DIIS extrapolation and direct minimization of the SCF energy is $10^{-\mbox{{\small THRESH\_ DIIS\_ SWITCH}}}$ when SCF_ALGORITHM is DIIS_GDM or DIIS_DM. See also MAX_DIIS_CYCLES


TYPE:

INTEGER


DEFAULT:

2


OPTIONS:

User-defined.


RECOMMENDATION:

None


4.5.5 Direct Minimization (DM)

Direct minimization (DM) is a less sophisticated forerunner of the geometric direct minimization (GDM) method discussed in the previous section. DM does not properly step along great circles in the hyper-spherical space of orbital rotations, and therefore converges less rapidly and less robustly than GDM, in general. It is retained for legacy purposes, and because it is at present the only method available for restricted open shell (RO) SCF calculations in Q-Chem. In general, the input options are the same as for GDM, with the exception of the specification of SCF_ALGORITHM, which can be either DIIS_DM (recommended) or DM.

PSEUDO_CANONICAL

When SCF_ALGORITHM = DM, this controls the way the initial step, and steps after subspace resets are taken.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Use Roothaan steps when (re)initializing

TRUE

Use a steepest descent step when (re)initializing


RECOMMENDATION:

The default is usually more efficient, but choosing TRUE sometimes avoids problems with orbital reordering.


4.5.6 Maximum Overlap Method (MOM)

In general, the DIIS procedure is remarkably successful. One difficulty that is occasionally encountered is the problem of an SCF that occupies two different sets of orbitals on alternating iterations, and therefore oscillates and fails to converge. This can be overcome by choosing orbital occupancies that maximize the overlap of the new occupied orbitals with the set previously occupied. Q-Chem contains the maximum overlap method (MOM) [166], developed by Andrew Gilbert and Peter Gill now at the Australian National University.

MOM is therefore is a useful adjunct to DIIS in convergence problems involving flipping of orbital occupancies. It is controlled by the $rem variable MOM_START, which specifies the SCF iteration on which the MOM procedure is first enabled. There are two strategies that are useful in setting a value for MOM_START. To help maintain an initial configuration it should be set to start on the first cycle. On the other hand, to assist convergence it should come on later to avoid holding on to an initial configuration that may be far from the converged one.

The MOM-related $rem variables in full are the following:.

MOM_PRINT

Switches printing on within the MOM procedure.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Printing is turned off

TRUE

Printing is turned on.


RECOMMENDATION:

None


MOM_START

Determines when MOM is switched on to stabilize DIIS iterations.


TYPE:

INTEGER


DEFAULT:

0 (FALSE)


OPTIONS:

0 (FALSE)

MOM is not used

$n$

MOM begins on cycle $n$.


RECOMMENDATION:

Set to 1 if preservation of initial orbitals is desired. If MOM is to be used to aid convergence, an SCF without MOM should be run to determine when the SCF starts oscillating. MOM should be set to start just before the oscillations.


4.5.7 Relaxed Constraint Algorithm (RCA)

The relaxed constraint algorithm (RCA) is an ingenious and simple means of minimizing the SCF energy that is particularly effective in cases where the initial guess is poor. The latter is true, for example, when employing a user-specified basis (when the Core or GWH guess must be employed) or when near-degeneracy effects imply that the initial guess will likely occupy the wrong orbitals relative to the desired converged solution.

Briefly, RCA begins with the SCF problem as a constrained minimization of the energy as a function of the density matrix, 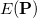$E(\mathbf{P})$ [167, 168]. The constraint is that the density matrix be idempotent, 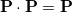$\mathbf{P} \cdot \mathbf{P}=\mathbf{P}$, which basically forces the occupation numbers to be either zero or one. The fundamental realization of RCA is that this constraint can be relaxed to allow sub-idempotent density matrices, 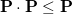$\mathbf{P} \cdot \mathbf{P} \leq \mathbf{P}$. This condition forces the occupation numbers to be between zero and one. Physically, we expect that any state with fractional occupations can lower its energy by moving electrons from higher energy orbitals to lower ones. Thus, if we solve for the minimum of 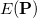$E(\mathbf{P})$ subject to the relaxed sub-idempotent constraint, we expect that the ultimate solution will nonetheless be idempotent. In fact, for Hartree-Fock this can be rigorously proven. For density functional theory, it is possible that the minimum will have fractional occupation numbers but these occupations have a physical interpretation in terms of ensemble DFT. The reason the relaxed constraint is easier to deal with is that it is easy to prove that a linear combination of sub-idempotent matrices is also sub-idempotent as long as the linear coefficients are between zero and one. By exploiting this property, convergence can be accelerated in a way that guarantees the energy will go down at every step.

The implementation of RCA in Q-Chem closely follows the “Energy DIIS” implementation of the RCA algorithm [169]. Here, the current density matrix is written as a linear combination of the previous density matrices:

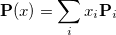  \begin{equation} \mathbf{P}(x) = \sum _ i x_ i \mathbf{P}_ i \end{equation}   (4.82)

To a very good approximation (exact for Hartree-Fock) the energy for 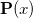$\mathbf{P}(x)$ can be written as a quadratic function of x:

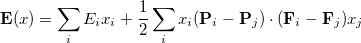  \begin{equation} \mathbf{E}(x) = \sum _ i E_ i x_ i+ \frac{1}{2} \sum _ i x_ i(\mathbf{P}_ i- \mathbf{P}_ j) \cdot (\mathbf{F}_ i- \mathbf{F}_ j) x_ j \end{equation}   (4.83)

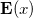At each iteration, $x$ is chosen to minimize $\mathbf{E}(x)$ subject to the constraint that all of the 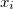$x_ i$ are between zero and one. The Fock matrix for 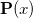$\mathbf{P}(x)$ is further written as a linear combination of the previous Fock matrices,

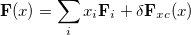  \begin{equation} \mathbf{F}(x) = \sum _ i x_ i \mathbf{F}_ i + \delta \mathbf{F}_{xc}(x) \end{equation}   (4.84)

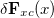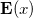where $\delta \mathbf{F}_{xc}(x)$ denotes a (usually quite small) change in the exchange-correlation part that is computed once $x$ has been determined. We note that this extrapolation is very similar to that used by DIIS. However, this procedure is guaranteed to reduce the energy $\mathbf{E}(x)$ at every iteration, unlike DIIS.

In practice, the RCA approach is ideally suited to difficult convergence situations because it is immune to the erratic orbital swapping that can occur in DIIS. On the other hand, RCA appears to perform relatively poorly near convergence, requiring a relatively large number of steps to improve the precision of a “good” approximate solution. It is thus advantageous in many cases to run RCA for the initial steps and then switch to DIIS either after some specified number of iterations or after some target convergence threshold has been reached. Finally, note that by its nature RCA considers the energy as a function of the density matrix. As a result, it cannot be applied to restricted open shell calculations which are explicitly orbital-based. Note: RCA interacts poorly with INCDFT, so INCDFT is disabled by default when an RCA or RCA_DIIS calculation is requested. To enable INCDFT with such a calculation, set INCDFT = 2 in the $rem section. RCA may also have poor interactions with INCFOCK; if RCA fails to converge, disabling INCFOCK may improve convergence in some cases.

RCA options are:

RCA_PRINT

Controls the output from RCA SCF optimizations.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

No print out

1

RCA summary information

2

Level 1 plus RCA coefficients

3

Level 2 plus RCA iteration details


RECOMMENDATION:

None


MAX_RCA_CYCLES

The maximum number of RCA iterations before switching to DIIS when SCF_ALGORITHM is RCA_DIIS.


TYPE:

INTEGER


DEFAULT:

50


OPTIONS:

N

N RCA iterations before switching to DIIS


RECOMMENDATION:

None


THRESH_RCA_SWITCH

The threshold for switching between RCA and DIIS when SCF_ALGORITHM is RCA_DIIS.


TYPE:

INTEGER


DEFAULT:

3


OPTIONS:

N

Algorithm changes from RCA to DIIS when Error is less than $10^{-N}$.


RECOMMENDATION:

None


Please see next section for an example using RCA.

4.5.8 Small-Gap Systems

SCF calculations for systems with zero or small HOMO-LUMO gap (such as metals) can exhibit very slow convergence or may even fail to converge. This problem arises because the energetic ordering of orbitals and states can switch during the SCF optimization leading to discontinuities in the optimization. Using fractional MO occupation numbers can improve the convergence for small-gap systems. In this approach, the occupation numbers of MOs around the Fermi level are allowed to assume non-integer values. This “occupation smearing” allows one to include multiple electron configurations in the same optimization, which improves the stability of the optimization.

We follow the pseudo-Fractional Occupation Number (pFON) method of Rabuck and Scuseria [170] that scales the MO occupation used to construct the AO density:

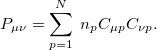  \begin{equation} P_{\mu \nu } = \sum _{p=1}^{N} \; n_{p} C_{\mu p} C_{\nu p}. \end{equation}   (4.85)

For a conventional (integer occupation number) SCF run, the occupation number 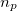$n_{p}$ is either one (occupied) or zero (virtual). In pFON, the occupation numbers are following a Fermi-Dirac distribution,

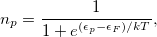  \begin{equation} n_{p} = \frac{1}{1 + e^{(\epsilon _{p} - \epsilon _{F})/kT}}, \end{equation}   (4.86)

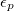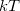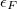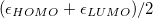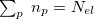where $\epsilon _{p}$ is the respective orbital energy and $kT$ the Boltzmann constant and temperature, respectively. The Fermi energy $\epsilon _{F}$ is set to $(\epsilon _{HOMO} + \epsilon _{LUMO})/2$ in our implementation. To ensure conservation of the total number of electrons, the pFON approach rescales the occupation numbers so that $\sum _{p} \; n_{p} = N_{el}$.

There are several parameters to control the electronic temperature 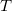$T$ throughout a pFON SCF run. The temperature can either be held constant at finite temperature (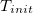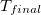$T_{init}$ = $T_{final}$), or the system can be cooled from a higher temperature down to the final temperature. So far, no zero-temperature extrapolation has been implemented.

OCCUPATIONS

Activates pFON calculation.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Integer occupation numbers

1

Not yet implemented

2

Pseudo-fractional occupation numbers (pFON)


RECOMMENDATION:

Use pFON to improve convergence for small-gap systems.


FON_T_START

Initial electronic temperature (in K) for FON calculation.


TYPE:

INTEGER


DEFAULT:

1000


OPTIONS:

Any desired initial temperature.


RECOMMENDATION:

Pick the temperature to either reproduce experimental conditions (e.g. room temperature) or as low as possible to approach zero-temperature.


FON_T_END

Final electronic temperature for FON calculation.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

Any desired final temperature.


RECOMMENDATION:

Pick the temperature to either reproduce experimental conditions (e.g. room temperature) or as low as possible to approach zero-temperature.


FON_NORB

Number of orbitals above and below the Fermi level that are allowed to have fractional occupancies.


TYPE:

INTEGER


DEFAULT:

4


OPTIONS:

n

number of active orbitals


RECOMMENDATION:

The number of valence orbitals is a reasonable choice.


FON_T_SCALE

Determines the step size for the cooling.


TYPE:

INTEGER


DEFAULT:

90


OPTIONS:

n

temperature is scaled by $0.01 \cdot n$ in each cycle (cooling method 1)

n

temperature is decreased by n K in each cycle (cooling method 2)


RECOMMENDATION:

The cooling rate should be neither too slow nor too fast. Too slow may lead to final energies that are at undesirably high temperatures. Too fast may lead to convergence issues. Reasonable choices for methods 1 and 2 are 98 and 50, respectively. When in doubt, use constant temperature.


FON_E_THRESH

DIIS error below which occupations will be kept constant.


TYPE:

INTEGER


DEFAULT:

4


OPTIONS:

n

freeze occupations below DIIS error of $10^{-n}$


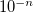
RECOMMENDATION:

This should be one or two numbers bigger than the desired SCF convergence threshold.


FON_T_METHOD

Selects cooling algorithm.


TYPE:

INTEGER


DEFAULT:

1


OPTIONS:

1

temperature is scaled by a factor in each cycle

2

temperature is decreased by a constant number in each cycle


RECOMMENDATION:

We have made slightly better experience with a constant cooling rate. However, choose constant temperature when in doubt.


4.5.9 Examples

Example 4.61  Input for a UHF calculation using geometric direct minimization (GDM) on the phenyl radical, after initial iterations with DIIS. This example fails to converge if DIIS is employed directly.

$molecule
   0   2
   c1
   x1  c1  1.0
   c2  c1  rc2  x1  90.0
   x2  c2  1.0  c1  90.0  x1    0.0
   c3  c1  rc3  x1  90.0  c2    tc3
   c4  c1  rc3  x1  90.0  c2   -tc3
   c5  c3  rc5  c1   ac5  x1  -90.0
   c6  c4  rc5  c1   ac5  x1   90.0
   h1  c2  rh1  x2  90.0  c1  180.0
   h2  c3  rh2  c1   ah2  x1   90.0
   h3  c4  rh2  c1   ah2  x1  -90.0
   h4  c5  rh4  c3   ah4  c1  180.0
   h5  c6  rh4  c4   ah4  c1  180.0
   
   rc2 =   2.672986
   rc3 =   1.354498
   tc3 =  62.851505
   rc5 =   1.372904
   ac5 = 116.454370
   rh1 =   1.085735
   rh2 =   1.085342
   ah2 = 122.157328
   rh4 =   1.087216
   ah4 = 119.523496
$end

$rem
   BASIS           = 6-31G*
   METHOD          = hf
   INTSBUFFERSIZE  = 15000000
   SCF_ALGORITHM   = diis_gdm
   SCF_CONVERGENCE = 7
   THRESH          = 10
$end

Example 4.62  An example showing how to converge a ROHF calculation on the 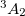$^3A_2$ state of DMX. Note the use of reading in orbitals from a previous closed-shell calculation and the use of MOM to maintain the orbital occupancies. The 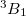$^3B_1$ is obtained if MOM is not used.

$molecule
  +1 1
   C       0.000000     0.000000     0.990770
   H       0.000000     0.000000     2.081970
   C      -1.233954     0.000000     0.290926
   C      -2.444677     0.000000     1.001437
   H      -2.464545     0.000000     2.089088
   H      -3.400657     0.000000     0.486785
   C      -1.175344     0.000000    -1.151599
   H      -2.151707     0.000000    -1.649364
   C       0.000000     0.000000    -1.928130
   C       1.175344     0.000000    -1.151599
   H       2.151707     0.000000    -1.649364
   C       1.233954     0.000000     0.290926
   C       2.444677     0.000000     1.001437
   H       2.464545     0.000000     2.089088
   H       3.400657     0.000000     0.486785
$end

$rem
   UNRESTRICTED      false
   METHOD            hf
   BASIS             6-31+G*
   SCF_GUESS         core
$end

@@@

$molecule
   read
$end

$rem
   UNRESTRICTED      false
   METHOD            hf
   BASIS             6-31+G*
   SCF_GUESS         read 
   MOM_START         1
$end

$occupied
1:26 28 
1:26 28 
$end

@@@

$molecule
-1 3
   ... <as above> ...
$end

$rem
   UNRESTRICTED      false
   METHOD            hf 
   BASIS             6-31+G*
   SCF_GUESS         read
$end

Example 4.63  RCA_DIIS algorithm applied a radical

$molecule
0 2
   H           1.004123   -0.180454    0.000000
   O          -0.246002    0.596152    0.000000
   O          -1.312366   -0.230256    0.000000
$end

$rem
   UNRESTRICTED            true
   METHOD                  hf
   BASIS                   cc-pVDZ
   SCF_GUESS               gwh
   SCF_ALGORITHM           RCA_DIIS
   DIIS_SUBSPACE_SIZE      15
   THRESH                  9
$end

Example 4.64  pFON calculation of a metal cluster.

$molecule
0 1
Pt        -0.20408        1.19210        0.54029
Pt         2.61132        1.04687        0.66196
Pt         0.83227        0.03296       -1.49084
Pt         0.95832       -1.05360        0.92253
Pt        -1.66760       -1.07875       -1.02416
$end

$rem
  jobtyp sp
  method PBE
  ecp lanl2dz
  BASIS      lanl2dz
  Maxscf 2000
  symmetry 0
  occupations 2 ! pseudo-fractional occupation numbers
  FON_NORB 10
  FON_T_START 300  ! electronic temperature: 300 K
  FON_T_END   300
  FON_E_THRESH 5   ! freeze occupation numbers once DIIS error is 10^-5
$end