6.8 Correlated Excited State Methods: ADC( ) Family
) Family
The ADC( ) family of correlated excited state methods is a series of size-extensive excited state methods based on perturbation theory. Each order
) family of correlated excited state methods is a series of size-extensive excited state methods based on perturbation theory. Each order  of ADC presents the excited state equivalent to the well-known
of ADC presents the excited state equivalent to the well-known  th order Møller-Plesset perturbation theory for the ground state. Currently, the ADC variants ADC(0), ADC(1), ADC(2)-s and ADC(2)-x are implemented into Q-Chem. The "resolution-of-the-identity" approximation can be used with any ADC variant. Additionally, there are spin-opposite scaling versions of both ADC(2) variants available.
th order Møller-Plesset perturbation theory for the ground state. Currently, the ADC variants ADC(0), ADC(1), ADC(2)-s and ADC(2)-x are implemented into Q-Chem. The "resolution-of-the-identity" approximation can be used with any ADC variant. Additionally, there are spin-opposite scaling versions of both ADC(2) variants available.
6.8.1 The Algebraic Diagrammatic Construction (ADC) Scheme
The Algebraic Diagrammatic Construction (ADC) scheme of the polarization propagator is an excited state method originating from Green’s function theory. It has first been derived employing the diagrammatic perturbation expansion of the polarization propagator using the Møller-Plesset partition of the Hamiltonian [381]. An alternative derivation is available in terms of the intermediate state representation (ISR) [382] which will be presented in the following.
As starting point for the derivation of ADC equations via ISR serves the exact N electron ground state 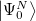 . From
. From 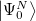 a complete set of correlated excited states is obtained by applying physical excitation operators
a complete set of correlated excited states is obtained by applying physical excitation operators 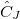 .
.
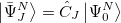 |
(6.48) |
with
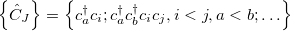 |
(6.49) |
Yet, the resulting excited states do not form an orthonormal basis. To construct an orthonormal basis out of the 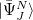 the Gram-Schmidt orthogonalization scheme is employed successively on the excited states in the various excitation classes starting from the exact ground state, the singly excited states, the doubly excited states etc.. This procedure eventually yields the basis of intermediate states
the Gram-Schmidt orthogonalization scheme is employed successively on the excited states in the various excitation classes starting from the exact ground state, the singly excited states, the doubly excited states etc.. This procedure eventually yields the basis of intermediate states 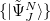 in which the Hamiltonian of the system can be represented forming the hermitian ADC matrix
in which the Hamiltonian of the system can be represented forming the hermitian ADC matrix
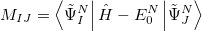 |
(6.50) |
Here, the Hamiltonian of the system is shifted by the exact ground state energy 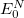 . The solution of the secular ISR equation
. The solution of the secular ISR equation
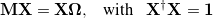 |
(6.51) |
yields the exact excitation energies 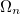 as eigenvalues. From the eigenvectors the exact excited states in terms of the intermediate states can be constructed as
as eigenvalues. From the eigenvectors the exact excited states in terms of the intermediate states can be constructed as
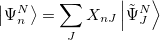 |
(6.52) |
This also allows for the calculation of dipole transition moments via
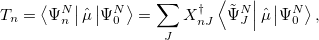 |
(6.53) |
as well as excited state properties via
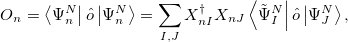 |
(6.54) |
where 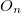 is the property associated with operator
is the property associated with operator 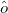 .
.
Up to now, the exact  -electron ground state has been employed in the derivation of the ADC scheme, thereby resulting in exact excitation energies and exact excited state wavefunctions. Since the exact ground state is usually not known, a suitable approximation must be used in the derivation of the ISR equations. An obvious choice is the
-electron ground state has been employed in the derivation of the ADC scheme, thereby resulting in exact excitation energies and exact excited state wavefunctions. Since the exact ground state is usually not known, a suitable approximation must be used in the derivation of the ISR equations. An obvious choice is the  th order Møller-Plesset ground state yielding the
th order Møller-Plesset ground state yielding the  th order approximation of the ADC scheme. The appropriate ADC equations have been derived in detail up to third order in Refs. Trofimov:1995,Trofimov:1999,Trofimov:2002. Due to the dependency on the Møller-Plesset ground state the
th order approximation of the ADC scheme. The appropriate ADC equations have been derived in detail up to third order in Refs. Trofimov:1995,Trofimov:1999,Trofimov:2002. Due to the dependency on the Møller-Plesset ground state the  th order ADC scheme should only be applied to molecular systems whose ground state is well described by the respective MP(
th order ADC scheme should only be applied to molecular systems whose ground state is well described by the respective MP( ) method.
) method.
As in Møller-Plesset perturbation theory, the first ADC scheme which goes beyond the non-correlated wavefunction methods in Section 6.2 is ADC(2). ADC(2) is available in a strict and an extended variant which are usually referred to as ADC(2)-s and ADC(2)-x, respectively. The strict variant ADC(2)-s scales with the 5th power of the basis set. The quality of ADC(2)-s excitation energies and corresponding excited states is comparable to the quality of those obtained with CIS(D) (Section 6.6) or CC2. More precisely, excited states with mostly single excitation character are well-described by ADC(2)-s, while excited states with double excitation character are usually found to be too high in energy. The ADC(2)-x variant which scales as the sixth power of the basis set improves the treatment of doubly excited states, but at the cost of introducing an imbalance between singly and doubly excited states. As result, the excitation energies of doubly excited states are substantially decreased in ADC(2)-x relative to the states possessing mostly single excitation character with the excitation energies of both types of states exhibiting relatively large errors. Still, ADC(2)-x calculations can be used as a diagnostic tool for the importance doubly excited states in the low-energy region of the spectrum by comparing to ADC(2)-s results. A significantly better description of both singly and doubly excited states is provided by the third order ADC scheme ADC(3). The accuracy of excitation energies obtained with ADC(3) is almost comparable to CC3, but at computational costs that scale with the sixth power of the basis set only [386].
6.8.2 Resolution of the Identity ADC Methods
Similar to MP2 and CIS(D), the ADC equations can be reformulated using the resolution-of-the-identity (RI) approximation. This significantly reduces the cost of the integral transformation and the storage requirements. Although it does not change the overall computational scaling of 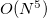 for ADC(2)-s or
for ADC(2)-s or 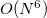 for ADC(2)-x with the system size, employing the RI approximation will result in computational speed-up of calculations of larger systems.
for ADC(2)-x with the system size, employing the RI approximation will result in computational speed-up of calculations of larger systems.
The RI approximation can be used with all available ADC methods. It is invoked as soon as an auxiliary basis set is specified using AUX_BASIS.
6.8.3 Spin Opposite Scaling ADC(2) Models
The spin-opposite scaling (SOS) approach originates from MP2 where it was realized that the same spin contributions can be completely neglected, if the opposite spin components are scaled appropriately. In a similar way it is possible to simplify the second order ADC equations by neglecting the same spin contributions in the ADC matrix, while the opposite-spin contributions are scaled with appropriate semi-empirical parameters. [387, 388, 389]
Starting from the SOS-MP2 ground state the same scaling parameter 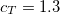 is introduced into the ADC equations to scale the
is introduced into the ADC equations to scale the 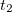 amplitudes. This alone, however, does not result in any computational savings or substantial improvements of the ADC(2) results. In addition, the opposite spin components in the ph/2p2h and 2p2h/ph coupling blocks have to be scaled using a second parameter
amplitudes. This alone, however, does not result in any computational savings or substantial improvements of the ADC(2) results. In addition, the opposite spin components in the ph/2p2h and 2p2h/ph coupling blocks have to be scaled using a second parameter 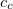 to obtain a useful SOS-ADC(2)-s model. With this model the optimal value of the parameter
to obtain a useful SOS-ADC(2)-s model. With this model the optimal value of the parameter 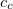 has been found to be 1.17 for the calculation of singlet excited states.[388]
has been found to be 1.17 for the calculation of singlet excited states.[388]
To extend the SOS approximation to the ADC(2)-x method yet another scaling parameter 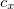 for the opposite spin components of the off-diagonal elements in the 2p2h/2p2h block has to be introduced. Here, the optimal values of the scaling parameters have been determined as
for the opposite spin components of the off-diagonal elements in the 2p2h/2p2h block has to be introduced. Here, the optimal values of the scaling parameters have been determined as  and
and  keeping
keeping 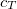 unchanged.[389]
unchanged.[389]
The spin-opposite scaling models can be invoked by setting METHOD to either SOSADC(2) or SOSADC(2)-x. By default, the scaling parameters are chosen as the optimal values reported above, i.e. 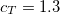 and
and 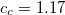 for ADC(2)-s and
for ADC(2)-s and 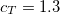 ,
,  , and
, and  for ADC(2)-x. However, it is possible to adjust any of the three parameters by setting ADC_C_T, ADC_C_C, or ADC_C_X, respectively.
for ADC(2)-x. However, it is possible to adjust any of the three parameters by setting ADC_C_T, ADC_C_C, or ADC_C_X, respectively.
6.8.4 Core-Excitation ADC Methods
Core-excited electronic states are located in the high energy X-ray region of the spectrum. Thus, to compute core-excited states using standard diagonalization procedures, which usually solve for the energetically lowest-lying excited states first, requires the calculation of a multitude of excited states. This is computationally very expensive and only feasible for calculations on very small molecules and small basis sets.
The core-valence separation (CVS) approximation solves the problem by neglecting the couplings between core and valence excited states a priori. Thereby, the ADC matrix acquires a certain block structure which allows to solve only for core-excited states. The application of the CVS approximation is justified, since core and valence excited states are energetically well separated and the coupling between both types of states is very small. To achieve the separation of core and valence excited states the CVS approximation forces the following types of two-electron integrals to zero
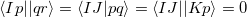 |
(6.55) |
where capital letters 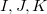 refer to core orbitals while lower-case letters
refer to core orbitals while lower-case letters 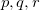 denote non-core occupied or virtual orbitals.
denote non-core occupied or virtual orbitals.
The core-valence approximation is currently available of ADC models up to second order (including the extended variant). It can be invoked by setting METHOD to the respective ADC model prefixed by CVS.
6.8.5 Properties and Visualization
The calculation of excited states using the ADCMAN module yields by default the usual excitation energies and the excitation amplitudes, as well as the transition dipole moments, oscillator strengths, and the norm of the doubles part of the amplitudes (if applicable). In addition, the calculation of excited state properties, like dipole moments, and transition properties between excited states can be requested by setting the $rem variables ADC_PROP_ES and ADC_PROP_ES2ES, respectively. Resonant two-photon absorption cross-sections of the excited states can be computed as well, using either sum-over-states expressions or the matrix inversion technique. The calculation via sum-over-state expressions is automatically activated, if ADC_PROP_ES2ES is set. The accuracy of the results, however, strongly depends on the number of states which are included in the summation, i.e. the number of states computed. At least, 20-30 excited states (per irreducible representation) are required to yield useful results for the two-photon absorption cross-sections. Alternatively, the resonant two-photon absorption cross-sections can be calculated by setting ADC_PROP_TPA to TRUE. In this case, the computation of a large number of excited states is avoided and there is no dependence on the number of excited states. Instead, an additional linear matrix equation has to be solved for every excited state for which the two-photon absorption cross-section is computed. Thus, the obtained resonant two-photon absorption cross-sections are usually more reliable.
Furthermore, the ADCMAN module allows for the detailed analysis of the excited states and export of various types of excited state related orbitals and densities. This can be activated by setting the keyword STATE_ANALYSIS. Details on the available analyses and export options can be found in section 10.2.7.
6.8.6 ADC Job Control
For an ADC calculation it is important to ensure that there are sufficient resources available for the necessary integral calculations and transformations. These resources are controlled using the $rem variables MEM_STATIC and MEM_TOTAL. The memory used by ADC is currently 95% of the difference MEM_TOTAL - MEM_STATIC.
An ADC calculation is requested by setting the $rem variable METHOD to the respective ADC variant. Furthermore, the number of excited states to be calculated has to be specified using one of the $rem variables EE_STATES, EE_SINGLETS, or EE_TRIPLETS. The former variable should be used for open-shell or unrestricted closed-shell calculations, while the latter two variables are intended for restricted closed-shell calculations. Even though not recommended, it is possible to use EE_STATES in a restricted calculation which translates into EE_SINGLETS, if neither EE_SINGLETS nor EE_TRIPLETS is set. Similarly, the use EE_SINGLETS in an unrestricted calculation will translate into EE_STATES, if the latter is not set as well.
All $rem variables to set the number of excited states accept either an integer number or a vector of integer numbers. A single number specifies that the same number of excited states are calculated for every irreducible representation the point group of the molecular system possesses (molecules without symmetry are treated as  symmetric). In contrast, a vector of numbers determines the number of states for each irreducible representation explicitly. Thus, the length of the vector always has to match the number of irreducible representations. Hereby, the excited states are labeled according to the irreducible representation of the electronic transition which might be different from the irreducible representation of the excited state wave function. Users can choose to calculate any molecule as
symmetric). In contrast, a vector of numbers determines the number of states for each irreducible representation explicitly. Thus, the length of the vector always has to match the number of irreducible representations. Hereby, the excited states are labeled according to the irreducible representation of the electronic transition which might be different from the irreducible representation of the excited state wave function. Users can choose to calculate any molecule as  symmetric by setting CC_SYMMETRY to FALSE.
symmetric by setting CC_SYMMETRY to FALSE.
METHOD
Controls the order in perturbation theory of ADC.
TYPE:
STRING
DEFAULT:
None
OPTIONS:
ADC(1)
Perform ADC(1) calculation.
ADC(2)
Perform ADC(2)-s calculation.
ADC(2)-x
Perform ADC(2)-x calculation.
ADC(3)
Perform ADC(3) calculation.
SOS-ADC(2)
Perform spin-opposite scaled ADC(2)-s calculation.
SOS-ADC(2)-x
Perform spin-opposite scaled ADC(2)-x calculation.
CVS-ADC(1)
Perform ADC(1) calculation of core excitations.
CVS-ADC(2)
Perform ADC(2)-s calculation of core excitations.
CVS-ADC(2)-x
Perform ADC(2)-x calculation of core excitations.
RECOMMENDATION:
None
EE_STATES
Controls the number of excited states to calculate.
TYPE:
INTEGER
DEFAULT:
0
Do not perform an ADC calculation
OPTIONS:
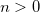
Number of states to calculate for each irrep or
![$[n_1, n_2, ...]$](images/img-0840.png)
Compute
states for the first irrep,
states for the second irrep, ...
RECOMMENDATION:
Use this variable to define the number of excited states in case of unrestricted or open-shell calculations. In restricted calculations it can also be used, if neither EE_SINGLETS nor EE_TRIPLETS is given. Then, it has the same effect as setting EE_SINGLETS.
EE_SINGLETS
Controls the number of singlet excited states to calculate.
TYPE:
INTEGER
DEFAULT:
0
Do not perform an ADC calculation of singlet excited states
OPTIONS:
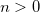
Number of singlet states to calculate for each irrep or
![$[n_1, n_2, ...]$](images/img-0840.png)
Compute
states for the first irrep,
states for the second irrep, ...
RECOMMENDATION:
Use this variable to define the number of excited states in case of restricted calculations of singlet states. In unrestricted calculations it can also be used, if EE_STATES not set. Then, it has the same effect as setting EE_STATES.
EE_TRIPLETS
Controls the number of triplet excited states to calculate.
TYPE:
INTEGER/INTEGER ARRAY
DEFAULT:
0
Do not perform an ADC calculation of triplet excited states
OPTIONS:
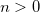
Number of triplet states to calculate for each irrep or
![$[n_1, n_2, ...]$](images/img-0840.png)
Compute
states for the first irrep,
states for the second irrep, ...
RECOMMENDATION:
Use this variable to define the number of excited states in case of restricted calculations of triplet states.
CC_SYMMETRY
Activates point-group symmetry in the ADC calculation.
TYPE:
LOGICAL
DEFAULT:
TRUE
If the system possesses any point-group symmetry.
OPTIONS:
TRUE
Employ point-group symmetry
FALSE
Do not use point-group symmetry
RECOMMENDATION:
None
ADC_PROP_ES
Controls the calculation of excited state properties (currently only dipole moments).
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate excited state properties.
FALSE
Do not compute state properties.
RECOMMENDATION:
Set to TRUE, if properties are required.
ADC_PROP_ES2ES
Controls the calculation of transition properties between excited states (currently only transition dipole moments and oscillator strengths), as well as the computation of two-photon absorption cross-sections of excited states using the sum-over-states expression.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate state-to-state transition properties.
FALSE
Do not compute transition properties between excited states.
RECOMMENDATION:
Set to TRUE, if state-to-state properties or sum-over-states two-photon absorption cross-sections are required.
ADC_PROP_TPA
Controls the calculation of two-photon absorption cross-sections of excited states using matrix inversion techniques.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Calculate two-photon absorption cross-sections.
FALSE
Do not compute two-photon absorption cross-sections.
RECOMMENDATION:
Set to TRUE, if to obtain two-photon absorption cross-sections.
STATE_ANALYSIS
Controls the analysis and export of excited state densities and orbitals (see 10.2.7 for details).
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Perform excited state analyses.
FALSE
No excited state analyses or export will be performed.
RECOMMENDATION:
Set to TRUE, if detailed analysis of the excited states is required or if density or orbital plots are needed.
ADC_C_T
Set the spin-opposite scaling parameter
for an SOS-ADC(2) calculation. The parameter value is obtained by multiplying the given integer by
.
TYPE:
INTEGER
DEFAULT:
1300
Optimized value
.
OPTIONS:

Corresponding to
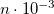
RECOMMENDATION:
Use default
ADC_C_C
Set the spin-opposite scaling parameter
for the ADC(2) calculation. The parameter value is obtained by multiplying the given integer by
.
TYPE:
INTEGER
DEFAULT:
1170
Optimized value
for ADC(2)-s or
1000
for ADC(2)-x
OPTIONS:

Corresponding to
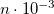
RECOMMENDATION:
Use default
ADC_C_X
Set the spin-opposite scaling parameter
for the ADC(2)-x calculation. The parameter value is obtained by multiplying the given integer by
.
TYPE:
INTEGER
DEFAULT:
1300
Optimized value
for ADC(2)-x.
OPTIONS:

Corresponding to
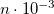
RECOMMENDATION:
Use default
ADC_NGUESS_SINGLES
Controls the number of excited state guess vectors which are single excitations. If the number of requested excited states exceeds the total number of guess vectors (singles and doubles), this parameter is automatically adjusted, so that the number of guess vectors matches the number of requested excited states.
TYPE:
INTEGER
DEFAULT:
Equals to the number of excited states requested.
OPTIONS:

User-defined integer.
RECOMMENDATION:
ADC_NGUESS_DOUBLES
Controls the number of excited state guess vectors which are double excitations.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:

User-defined integer.
RECOMMENDATION:
ADC_DO_DIIS
Activates the use of the DIIS algorithm for the calculation of ADC(2) excited states.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE
Use DIIS algorithm.
FALSE
Do diagonalization using Davidson algorithm.
RECOMMENDATION:
None.
ADC_DIIS_START
Controls the iteration step at which DIIS is turned on.
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:

User-defined integer.
RECOMMENDATION:
Set to a large number to switch off DIIS steps.
ADC_DIIS_SIZE
Controls the size of the DIIS subspace.
TYPE:
INTEGER
DEFAULT:
7
OPTIONS:

User-defined integer
RECOMMENDATION:
None
ADC_DIIS_MAXITER
Controls the maximum number of DIIS iterations.
TYPE:
INTEGER
DEFAULT:
50
OPTIONS:

User-defined integer.
RECOMMENDATION:
Increase in case of slow convergence.
ADC_DIIS_ECONV
Controls the convergence criterion for the excited state energy during DIIS.
TYPE:
INTEGER
DEFAULT:
6
Corresponding to
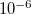
OPTIONS:

Corresponding to
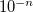
RECOMMENDATION:
None
ADC_DIIS_RCONV
Convergence criterion for the residual vector norm of the excited state during DIIS.
TYPE:
INTEGER
DEFAULT:
6
Corresponding to
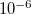
OPTIONS:

Corresponding to
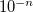
RECOMMENDATION:
None
ADC_DAVIDSON_MAXSUBSPACE
Controls the maximum subspace size for the Davidson procedure.
TYPE:
INTEGER
DEFAULT:
the number of excited states to be calculated.
OPTIONS:

User-defined integer.
RECOMMENDATION:
Should be at least
the number of excited states to calculate. The larger the value the more disk space is required.
ADC_DAVIDSON_MAXITER
Controls the maximum number of iterations of the Davidson procedure.
TYPE:
INTEGER
DEFAULT:
60
OPTIONS:

Number of iterations
RECOMMENDATION:
Use default unless convergence problems are encountered.
ADC_DAVIDSON_CONV
Controls the convergence criterion of the Davidson procedure.
TYPE:
INTEGER
DEFAULT:
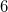
Corresponding to
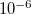
OPTIONS:

Corresponding to
.
RECOMMENDATION:
Use default unless higher accuracy is required or convergence problems are encountered.
ADC_DAVIDSON_THRESH
Controls the threshold for the norm of expansion vectors to be added during the Davidson procedure.
TYPE:
INTEGER
DEFAULT:
Twice the value of ADC_DAVIDSON_CONV, but at maximum
.
OPTIONS:

Corresponding to
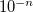
RECOMMENDATION:
Use default unless convergence problems are encountered. The threshold value
should always be smaller than the convergence criterion ADC_DAVIDSON_CONV.
ADC_PRINT
Controls the amount of printing during an ADC calculation.
TYPE:
INTEGER
DEFAULT:
1
Basic status information and results are printed.
OPTIONS:
0
Quiet: almost only results are printed.
1
Normal: basic status information and results are printed.
2
Debug1: more status information, extended information on timings.
...
RECOMMENDATION:
Use default.
6.8.7 Examples
Example 6.166 Q-Chem input for an ADC(2)-s calculation of singlet exited states of methane with D2 symmetry. In total six excited states are requested corresponding to four (two) electronic transitions with irreducible representation 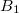 (
(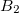 ).
).
$molecule
0 1
C
H 1 r0
H 1 r0 2 d0
H 1 r0 2 d0 3 d1
H 1 r0 2 d0 4 d1
r0 = 1.085
d0 = 109.4712206
d1 = 120.0
$end
$rem
jobtype sp
method adc(2)
basis 6-31g(d,p)
mem_total 4000
mem_static 100
ee_singlets [0,4,2,0]
$end
Example 6.167 Q-Chem input for an unrestricted RI-ADC(2)-s calculation with 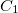 symmetry using DIIS. In addition, excited state properties and state-to-state properties are computed.
symmetry using DIIS. In addition, excited state properties and state-to-state properties are computed.
$molecule
0 2
C 0.0 0.0 -0.630969
N 0.0 0.0 0.540831
$end
$rem
jobtype sp
method adc(2)
basis aug-cc-pVDZ
aux_basis rimp2-aug-cc-pVDZ
mem_total 4000
mem_static 100
cc_symmetry false
ee_states 6
adc_do_diis true
adc_prop_es true
adc_prop_es2es true
adc_prop_tpa true
$end
Example 6.168 Q-Chem input for a restricted ADC(2)-x calculation of water with 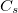 symmetry. Four singlet A" excited states and two triplet A’ excited states are requested. For the first two states (1
symmetry. Four singlet A" excited states and two triplet A’ excited states are requested. For the first two states (1 A" and 1
A" and 1 A’) the transition densities as well as the attachment and detachment densities are exported into cube files.
A’) the transition densities as well as the attachment and detachment densities are exported into cube files.
$molecule
0 1
O 0.000 0.000 0.000
H 0.000 0.000 0.950
H 0.896 0.000 -0.317
$end
$rem
jobtype sp
method adc(2)-x
basis 6-31g(d,p)
threads 2
mem_total 3000
mem_static 100
ee_singlets [0,4]
ee_triplets [2,0]
adc_prop_es true
make_cube_files true
$end
$plots
Plot transition and a/d densities
40 -3.0 3.0
40 -3.0 3.0
40 -3.0 3.0
0 0 2 2
1 2
1 2
$end