Q-Chem 4.3 User’s Manual

6.9 Restricted active space spin-flip (RAS-SF) and configuration interaction (RAS-CI) methods

The restricted active space spin-flip (RAS-SF) is a special form of configuration interaction that is capable of describing the ground and low-lying excited states with moderate computational cost in a single-reference formulation [390, 391, 392, 393], including strongly correlated systems. The RAS-SF approach is essentially a much lower computational cost alternative to Complete Active Space SCF (CAS-SCF) methods. RAS-SF typically works by performing a full CI calculation within an active space that is defined by the half-occupied orbitals of a restricted open shell HF (ROHF) reference determinant. In this way the difficulties of state-specific orbital optimization in CAS-SCF are bypassed. Single excitations into (hole) and out of (particle) the active space provide state-specific relaxation instead. Unlike most CI-based methods, RAS-SF is size-consistent, as well as variational, and, the increase in computational cost with system size is modest for a fixed number of spin flips. Beware, however, for the increase in cost as a function of the number of spin-flips is exponential! RAS-SF has been shown to be capable of tackling multiple low-lying electronic states in polyradicals and reliably predicting ground state multiplicities [390, 394, 395, 396, 391, 392].

RAS-SF can also be viewed as one particular case of a more general RAS-CI family of methods. For instance, instead of defining the active space via spin-flipping as above, initial orbitals of other types can be read in, and electronic excitations calculated this way may be viewed as a RAS-EE-CI method (though size-consistency will generally be lost). Similar to EOM-CC approaches (see Section 6.7), other target RAS-CI wavefunctions can be constructed starting from any electronic configuration as the reference and using a general excitation-type operator. For instance, one can construct an ionizing variant that removes an arbitrary number of particles that is RAS-$n$IP-CI. An electron attaching variant is RAS-$n$EA-CI [393].

Q-Chem features two versions of RAS-CI code with different, complementary, functionalities. One code (invoked by specifying CORR=RASCI) has been written by David Casanova [393]; below we will refer to this code as RASCI1. The second implementation (invoked by specifying CORR=RASCI2) is primarily by Paul Zimmerman [391]; we will refer to it as RASCI2 below.

The RASCI1 code uses an integral-driven implementation (exact integrals) and spin-adaptation of the CI configurations which results in a smaller diagonalization dimension. The current Q-Chem implementation of RASCI1 only allows for the calculation of systems with an even number of electrons, with the multiplicity of each state being printed alongside the state energy. Shared memory parallel execution decreases compute time as all the underlying integrals routines are parallelized.

The RASCI2 code includes the ability to simulate closed and open shell systems (i.e., even and odd numbers of electrons), fast integral evaluation using the resolution of the identity (RI) approximation, shared memory parallel operation, and analysis of the 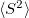$\langle S^2\rangle $ values and natural orbitals. The natural orbitals are stored in the QCSCRATCH directory in a folder called “NOs” in Molden-readable format. Shared memory parallel is invoked as described in Section 2.7.1. A RASCI2 input requires the specification of an auxiliary basis set analogous to RI-MP2 computations (see Section 5.5.1). Otherwise, the active space as well as hole and particle excitations are specified in the same way as in RASCI1.

Note: Because RASCI2 uses the RI approximation, the total energies computed with the two codes will be slightly different; however, the energy differences between different states should closely match each other.

6.9.1 The Restricted Active Space (RAS) Scheme

In the RAS formalism, we divide the orbital space into three subspaces called RAS1, RAS2 and RAS3 (Fig. 6.2). The RAS-CI states are defined by the number of orbitals and the restrictions in each subspace.

\begin{picture}(4,9)\thicklines \put(0,1.8){RAS1} \put(0,4.85){RAS2} \put(0,7.4){RAS3} \put(2.3,0.2){...} \put(2,1){\line(1,0){1}} \put(2,2){\line(1,0){1}} \put(2,3){\line(1,0){1}} \put(2.18,0.8){\Large {\ensuremath{\upharpoonleft }}\Large {\ensuremath{\downharpoonright }}} \put(2.18,1.8){\Large {\ensuremath{\upharpoonleft }}\Large {\ensuremath{\downharpoonright }}} \put(2.18,2.8){\Large {\ensuremath{\upharpoonleft }}\Large {\ensuremath{\downharpoonright }}} \put(2,4.5){\line(1,0){1}} \put(2,5.5){\line(1,0){1}} \put(2.18,4.3){\Large {\ensuremath{\upharpoonleft }}} \put(2.18,5.3){\Large {\ensuremath{\upharpoonleft }}} \put(2,7){\line(1,0){1}} \put(2,8){\line(1,0){1}} \put(2.3,8.7){...} \put(3.5,1.8){min $N-h$ electrons (holes)} \put(3.5,4.85){\textit{active space}} \put(3.5,7.4){max $p$ electrons (particles)} \end{picture}
Figure 6.2: Orbital subspaces in RAS-CI employing a ROHF triplet reference.

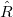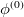The single reference RAS-CI electronic wavefunctions are obtained by applying a spin-flipping or excitation operator $\hat R$ on the reference determinant $\phi ^{\text {(0)}}$.

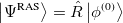  \begin{equation} \left|{\Psi }^{\text {RAS}}\right> = \hat{R} \left|\phi ^{\text {(0)}}\right> \end{equation}   (6.56)

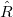The $\hat R$ operator must obey the restrictions imposed in the subspaces RAS1, RAS2 and RAS3, and can be decomposed as:

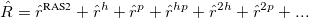  \begin{equation} \label{eqRoperator} \hat{R} = \hat r^{\text {RAS2}} + \hat r^ h + \hat r^ p + \hat r^{hp} + \hat r^{2h} + \hat r^{2p} +... \end{equation}   (6.57)

where 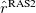$\hat r^{\text {RAS2}}$ contains all possible electronic promotions within the RAS2 space, that is, a reduced full CI, and the rest of the terms generate configurations with different number of holes (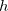$h$ superindex) in RAS1 and electrons in RAS3 (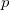$p$ superindex). The current implementation truncates this series up to the inclusion of hole and particle contributions, i.e. the first three terms on the right hand side of Eq. (6.57).

6.9.2 Job Control for the RASCI1 implementation

At present the RASCI1 and RASCI2 implementations employ different keywords (which will be reconciled in a future version). This subsection applies to RASCI1 (even electron systems, spin adapted algorithm using exact integrals).

The use of the RAS-CI1 methodology is controlled by setting the $rem variable CORRELATION to RASCI and EXCHANGE should be set to HF. The RASCI1 implementation is only compatible with even numbers of electrons and restricted orbitals, i.e., UNRESTRICTED = FALSE.

The minimum input also requires specifying the desired (non-zero) value for RAS_ROOTS, the number of electrons in the “active” RAS2 space and the number of orbitals in RAS1 and RAS2 subspaces.

RAS_ROOTS

Sets the number of RAS-CI roots to be computed.


TYPE:

INTEGER


DEFAULT:

None


OPTIONS:

$n$

$n>0$ Compute $n$ RAS-CI states


RECOMMENDATION:

None. Only works with RASCI.


RAS_ELEC

Sets the number of electrons in RAS2 (active electrons).


TYPE:

INTEGER


DEFAULT:

None


OPTIONS:

$n$

User-defined integer, $n>0$


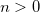
RECOMMENDATION:

None. Only works with RASCI.


RAS_ACT

Sets the number of orbitals in RAS2 (active orbitals).


TYPE:

INTEGER


DEFAULT:

None


OPTIONS:

$n$

User-defined integer, $n>0$


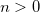
RECOMMENDATION:

None. Only works with RASCI.


RAS_OCC

Sets the number of orbitals in RAS1


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

$n$

User-defined integer, $n>0$


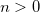
RECOMMENDATION:

These are the initial doubly occupied orbitals (RAS1) before including $hole$ type of excitations. The RAS1 space starts from the lowest orbital up to RAS_OCC, i.e. no frozen orbitals option available yet. Only works with RASCI.


RAS_DO_HOLE

Controls the presence of hole excitations in the RAS-CI wavefunction.


TYPE:

LOGICAL


DEFAULT:

TRUE


OPTIONS:

TRUE

Include hole configurations (RAS1 to RAS2 excitations)

FALSE

Do not include hole configurations


RECOMMENDATION:

None. Only works with RASCI.


RAS_DO_PART

Controls the presence of particle excitations in the RAS-CI wavefunction.


TYPE:

LOGICAL


DEFAULT:

TRUE


OPTIONS:

TRUE

Include particle configurations (RAS2 to RAS3 excitations)

FALSE

Do not include particle configurations


RECOMMENDATION:

None. Only works with RASCI.


RAS_AMPL_PRINT

Defines the absolute threshold ($\times 10^2$) for the CI amplitudes to be printed.


TYPE:

INTEGER


DEFAULT:

10

0.1 minimum absolute amplitude


OPTIONS:

$n$

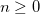
User-defined integer, $n\geq 0$


RECOMMENDATION:

None. Only works with RASCI.


RAS_ACT_ORB

Sets the user-selected active orbitals (RAS2 orbitals).


TYPE:

INTEGER ARRAY


DEFAULT:

From RAS_OCC+1 to RAS_OCC+RAS_ACT


OPTIONS:

$[i,j,k...]$

The number of orbitals must be equal to the RAS_ACT variable


RECOMMENDATION:

None. Only works with RASCI.


RAS_NATORB

Controls the computation of the natural orbital occupancies.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

TRUE

Compute natural orbital occupancies for all states

FALSE

Do not compute natural orbital occupancies


RECOMMENDATION:

None. Only works with RASCI.


RAS_NATORB_STATE

Allows to save the natural orbitals of a RAS-CI computed state.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

$i$

Saves the natural orbitals for the $i$-th state


RECOMMENDATION:

None. Only works with RASCI.


RAS_GUESS_CS

Controls the number of closed shell guess configurations in RAS-CI.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

$n$

Imposes to start with $n$ closed shell guesses


RECOMMENDATION:

Only relevant for the computation of singlet states. Only works with RASCI.


RAS_SPIN_MULT

Specifies the spin multiplicity of the roots to be computed


TYPE:

INTEGER


DEFAULT:

1

Singlet states


OPTIONS:

0

Compute any spin multiplicity

$2n+1$

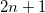
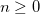
User-defined integer, $n\geq 0$


RECOMMENDATION:

Only for RASCI, which at present only allows for the computation of systems with an even number of electrons. Thus, RAS_SPIN_MULT only can take odd values.


6.9.3 Job control options for the RASCI2 implementation

At present the RASCI1 and RASCI2 implementations employ different keywords (which will be reconciled in a future version). This subsection applies to RASCI2 (even and odd electron systems, determinant-driven algorithm using the resolution of the identity approximation).

The use of the RAS-CI2 methodology is controlled by setting the CORRELATION = RASCI2 and EXCHANGE = HF. The minimum input also requires specifying the desired (non-zero) value for RAS_N_ROOTS, and the number of active occupied and virtual orbital comprising the “active” RAS2 space. RASCI2 calculations also require specification of an auxiliary basis via AUX_BASIS.

RAS_N_ROOTS

Sets the number of RAS-CI roots to be computed.


TYPE:

INTEGER


DEFAULT:

None


OPTIONS:

$n$

$n>0$ Compute $n$ RAS-CI states


RECOMMENDATION:

None. Only works with RASCI2


RAS_ACT_OCC

Sets the number of occupied orbitals to enter the RAS active space.


TYPE:

Integer


DEFAULT:

None


OPTIONS:

n

user defined integer


RECOMMENDATION:

None. Only works with RASCI2


RAS_ACT_VIR

Sets the number of virtual orbitals to enter the RAS active space.


TYPE:

Integer


DEFAULT:

None


OPTIONS:

n

user defined integer


RECOMMENDATION:

None. Only works with RASCI2.


RAS_ACT_DIFF

Sets the number of alpha vs. beta electrons


TYPE:

Integer


DEFAULT:

None


OPTIONS:

n

user defined integer


RECOMMENDATION:

Set to 1 for an odd number of electrons or a cation, -1 for an anion. Only works with RASCI2.


Other $rem variables that can be used to control the evaluation of RASCI2 calculations are SET_ITER for the maximum number of Davidson iterations, and N_FROZEN_CORE and N_FROZEN_VIRTUAL to exclude core and/or virtual orbitals from the RASCI2 calculation.

6.9.4 Examples

Example 6.169  Input for a RAS-2SF-CI calculation of three states of the DDMX tetraradical using RASCI1. The active space (RAS2) contains 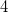$4$ electrons in the 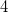$4$ singly occupied orbitals in the ROHF quintet reference. Natural orbital occupancies are requested.

$molecule
0 5
C      0.000000    0.000000    1.092150
C     -1.222482    0.000000    0.303960
C     -2.390248    0.000000    1.015958
H     -2.344570    0.000000    2.095067
H     -3.363161    0.000000    0.537932
C     -1.215393    0.000000   -1.155471
H     -2.150471    0.000000   -1.702536
C      0.000000    0.000000   -1.769131
C      1.215393    0.000000   -1.155471
H      2.150471    0.000000   -1.702536
C      1.222482    0.000000    0.303960
C      2.390248    0.000000    1.015958
H      2.344570    0.000000    2.095067
H      3.363161    0.000000    0.537932
$end

$rem
  jobtype       sp
  exchange      hf
  correlation   rasci
  basis         6-31g
  unrestricted  false
  mem_total     4000
  mem_static    100
  ras_roots     3
  ras_act       4
  ras_elec      4
  ras_occ       25
  ras_spin_mult 0
  ras_natorb    true
$end

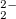Example 6.170  Input for a RAS-2IP-CI calculation of triplet states of F$_2$ molecule using the dianion closed shell F$_2^{2-}$ as the reference determinant. RASCI1 code is used

$molecule
-2 1
F
F  1  rFF

rFF = 1.4136
$end

$rem
  jobtype       sp
  exchange      hf
  correlation   rasci
  basis         cc-pVTZ
  mem_total     4000
  mem_static    100
  ras_roots     2
  ras_act       6
  ras_elec      10
  ras_occ       4
  ras_spin_mult 3
$end

Example 6.171  Input for a FCI/6-31G calculation of water molecule expanding the RAS2 space to the entire molecular orbital set. RASCI code is used.

$molecule
0 1
O   0.000  0.000   0.120
H  -0.762  0.000  -0.479
H   0.762  0.000  -0.479
$end

$rem
  jobtype        sp
  exchange       hf
  correlation    rasci
  basis          6-31G
  mem_total      4000
  mem_static     100
  ras_roots      1
  ras_act        13
  ras_elec       10
  ras_occ        0
  ras_spin_mult  1
  ras_do_hole    false
  ras_do_part    false
$end

Example 6.172  Methylene single spin-flip calculation using RASCI2

$rem
jobtype sp
exchange       HF
correlation    RASCI2
basis          cc-pVDZ
aux_basis      rimp2-cc-pVDZ
unrestricted   false

RAS_ACT_OCC    1    ! # alpha electrons
RAS_ACT_VIR    1    ! # virtuals in active space
RAS_ACT_DIFF   0    ! # set to 1 for odd # of e-s

ras_n_roots    4
set_iter       25   ! number of iterations in RASCI
$end


$molecule
0 3
C	0.0000000	0.0000000	0.0000000
H	-0.8611113	0.0000000	0.6986839
H	0.8611113	0.0000000	0.6986839
$end

Example 6.173  Two methylene separated by 10 ; double spin-flip calculation using RASCI2. Note that the 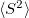$\langle S^2\rangle $ values for this case will not be uniquely defined at the triply-degenerate ground state.

$rem
exchange       HF
correlation    RASCI2

basis          cc-pVDZ
aux_basis      rimp2-cc-pVDZ

RAS_ACT_OCC    2    ! # alpha electrons
RAS_ACT_VIR    2    ! # virtuals in active space
RAS_ACT_DIFF   0    ! # set to 1 for odd # of e-s

unrestricted   false

jobtype sp

ras_n_roots    8
set_iter       25
$end

$molecule
0 5
C	0.0000000	0.0000000	0.0000000
H	-0.8611113	0.0000000	0.6986839
H	0.8611113	0.0000000	0.6986839
C	0.0000000	10.0000000	0.0000000
H	-0.8611113	10.0000000	0.6986839
H	0.8611113	10.0000000	0.6986839
$end

Example 6.174  RASCI2 calculation of the nitrogen cation using double spin-flip.

$rem
exchange HF
correlation RASCI2
jobtype sp

basis 6-31G*
aux_basis rimp2-VDZ

RAS_ACT_OCC 3    ! # alpha electrons
RAS_ACT_VIR 3    ! # virtuals in active space
RAS_ACT_DIFF 1   ! # for odd # e-s, cation

unrestricted false

n_frozen_core 2
n_frozen_virtual 2

ras_n_roots 8
set_iter      25
$end


$molecule
1 6
N	0.0000000	0.0000000	0.0000000
N	0.0000000	0.0000000	4.5
$end