6.2 Non-Correlated Wavefunction Methods
Q-Chem includes several excited state methods which do not incorporate correlation: CIS, XCIS and RPA. These methods are sufficiently inexpensive that calculations on large molecules are possible, and are roughly comparable to the HF treatment of the ground state in terms of performance. They tend to yield qualitative rather than quantitative insight. Excitation energies tend to exhibit errors on the order of an electron volt, consistent with the neglect of electron correlation effects, which are generally different in the ground state and the excited state.
6.2.1 Single Excitation Configuration Interaction (CIS)
The derivation of the CI-singles [308, 309] energy and wave function begins by selecting the HF single-determinant wavefunction as reference for the ground state of the system:
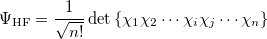 |
(6.1) |
where  is the number of electrons, and the spin orbitals
is the number of electrons, and the spin orbitals
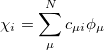 |
(6.2) |
are expanded in a finite basis of  atomic orbital basis functions. Molecular orbital coefficients
atomic orbital basis functions. Molecular orbital coefficients 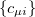 are usually found by SCF procedures which solve the Hartree-Fock equations
are usually found by SCF procedures which solve the Hartree-Fock equations
 |
(6.3) |
where S is the overlap matrix, C is the matrix of molecular orbital coefficients,  is a diagonal matrix of orbital eigenvalues and F is the Fock matrix with elements
is a diagonal matrix of orbital eigenvalues and F is the Fock matrix with elements
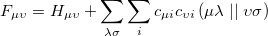 |
(6.4) |
involving the core Hamiltonian and the anti-symmetrized two-electron integrals
![\begin{equation} \label{eq604} \left( {\mu \nu \vert \vert \lambda \sigma } \right)=\int \int {\phi _\mu ({\rm {\bf r}}_{\rm {\bf 1}} )\phi _\nu ({\rm {\bf r}}_2 )\left( {1 {\left/ {{1 {r_{12} }}} \right. \kern -}\nulldelimiterspace0.0pt{r_{12} }} \right)\left[ {\phi _\lambda ({\rm {\bf r}}_1 )\phi _\sigma ({\rm {\bf r}}_{\rm {\bf 2}} )-\phi _\lambda ({\rm {\bf r}}_{\rm {\bf 2}} )\phi _\sigma ({\rm {\bf r}}_1 )} \right]d{\rm {\bf r}}_{\rm {\bf 1}} d{\rm {\bf r}}_{\rm {\bf 2}} } \end{equation}](images/img-0613.png) |
(6.5) |
On solving Eq. (6.3), the total energy of the ground state single determinant can be expressed as
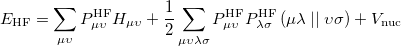 |
(6.6) |
where 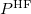 is the HF density matrix and
is the HF density matrix and 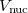 is the nuclear repulsion energy.
is the nuclear repulsion energy.
Equation (6.1) represents only one of many possible determinants made from orbitals of the system; there are in fact 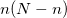 possible singly substituted determinants constructed by replacing an orbital occupied in the ground state (
possible singly substituted determinants constructed by replacing an orbital occupied in the ground state ( ,
, 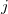 ,
, 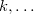 ) with an orbital unoccupied in the ground state (
) with an orbital unoccupied in the ground state ( ,
, 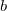 ,
,  ). Such wavefunctions and energies can be written
). Such wavefunctions and energies can be written
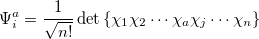 |
(6.7) |
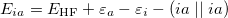 |
(6.8) |
where we have introduced the anti-symmetrized two-electron integrals in the molecular orbital basis
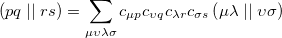 |
(6.9) |
These singly excited wavefunctions and energies could be considered crude approximations to the excited states of the system. However, determinants of the form Eq. (6.7) are deficient in that they:
do not yield pure spin states
resemble more closely ionization rather than excitation
are not appropriate for excitation into degenerate states
These deficiencies can be partially overcome by representing the excited state wavefunction as a linear combination of all possible singly excited determinants,
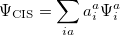 |
(6.10) |
where the coefficients 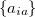 can be obtained by diagonalizing the many-electron Hamiltonian, A, in the space of all single substitutions. The appropriate matrix elements are:
can be obtained by diagonalizing the many-electron Hamiltonian, A, in the space of all single substitutions. The appropriate matrix elements are:
![\begin{equation} \label{eq610} A_{ia,jb} =\left\langle {\Psi _ i^ a } \right|H\left| {\Psi _ j^ b } \right\rangle =\left[ {E_{\ensuremath{\mathrm{HF}}} +\varepsilon _ a -\varepsilon _ j } \right]\delta _{ij} \delta _{ab} -\left( {ja} \right.\vert \vert \left. {ib} \right) \end{equation}](images/img-0625.png) |
(6.11) |
According to Brillouin’s, theorem single substitutions do not interact directly with a reference HF determinant, so the resulting eigenvectors from the CIS excited state represent a treatment roughly comparable to that of the HF ground state. The excitation energy is simply the difference between HF ground state energy and CIS excited state energies, and the eigenvectors of A correspond to the amplitudes of the single-electron promotions.
CIS calculations can be performed in Q-Chem using restricted (RCIS) [308, 309], unrestricted (UCIS), or restricted open shell (ROCIS) [310] spin orbitals.
6.2.2 Random Phase Approximation (RPA)
The Random Phase Approximation (RPA) [311, 312] also known as time-dependent Hartree-Fock (TD-HF) is an alternative to CIS for uncorrelated calculations of excited states. It offers some advantages for computing oscillator strengths, and is roughly comparable in accuracy to CIS for excitation energies to singlet states, but is inferior for triplet states. RPA energies are non-variational.
6.2.3 Extended CIS (XCIS)
The motivation for the extended CIS procedure (XCIS) [313] stems from the fact that ROCIS and UCIS are less effective for radicals that CIS is for closed shell molecules. Using the attachment/detachment density analysis procedure [314], the failing of ROCIS and UCIS methodologies for the nitromethyl radical was traced to the neglect of a particular class of double substitution which involves the simultaneous promotion of an  spin electron from the singly occupied orbital and the promotion of a
spin electron from the singly occupied orbital and the promotion of a 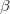 spin electron into the singly occupied orbital. The spin-adapted configurations
spin electron into the singly occupied orbital. The spin-adapted configurations
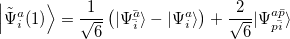 |
(6.12) |
are of crucial importance. (Here, 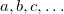 are virtual orbitals;
are virtual orbitals; 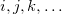 are occupied orbitals; and
are occupied orbitals; and 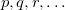 are singly-occupied orbitals.) It is quite likely that similar excitations are also very significant in other radicals of interest.
are singly-occupied orbitals.) It is quite likely that similar excitations are also very significant in other radicals of interest.
The XCIS proposal, a more satisfactory generalization of CIS to open shell molecules, is to simultaneously include a restricted class of double substitutions similar to those in Eq. (6.12). To illustrate this, consider the resulting orbital spaces of an ROHF calculation: doubly occupied (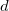 ), singly occupied (
), singly occupied ( ) and virtual (
) and virtual ( ). From this starting point we can distinguish three types of single excitations of the same multiplicity as the ground state:
). From this starting point we can distinguish three types of single excitations of the same multiplicity as the ground state: 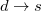 ,
, 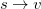 and
and 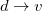 . Thus, the spin-adapted ROCIS wavefunction is
. Thus, the spin-adapted ROCIS wavefunction is
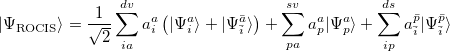 |
(6.13) |
The extension of CIS theory to incorporate higher excitations maintains the ROHF as the ground state reference and adds terms to the ROCIS wavefunction similar to that of Eq. (6.13), as well as those where the double excitation occurs through different orbitals in the  and
and 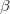 space:
space:
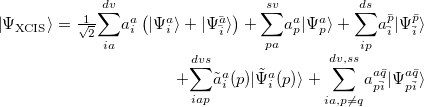 |
(6.14) |
XCIS is defined only from a restricted open shell Hartree-Fock ground state reference, as it would be difficult to uniquely define singly occupied orbitals in a UHF wavefunction. In addition,  unoccupied orbitals, through which the spin-flip double excitation proceeds, may not match the half-occupied
unoccupied orbitals, through which the spin-flip double excitation proceeds, may not match the half-occupied  orbitals in either character or even symmetry.
orbitals in either character or even symmetry.
For molecules with closed shell ground states, both the HF ground and CIS excited states emerge from diagonalization of the Hamiltonian in the space of the HF reference and singly excited substituted configuration state functions. The XCIS case is different because the restricted class of double excitations included could mix with the ground state and lower its energy. This mixing is avoided to maintain the size consistency of the ground state energy.
With the inclusion of the restricted set of doubles excitations in the excited states, but not in the ground state, it could be expected that some fraction of the correlation energy be recovered, resulting in anomalously low excited state energies. However, the fraction of the total number of doubles excitations included in the XCIS wavefunction is very small and those introduced cannot account for the pair correlation of any pair of electrons. Thus, the XCIS procedure can be considered one that neglects electron correlation.
The computational cost of XCIS is approximately four times greater than CIS and ROCIS, and its accuracy for open shell molecules is generally comparable to that of the CIS method for closed shell molecules. In general, it achieves qualitative agreement with experiment. XCIS is available for doublet and quartet excited states beginning from a doublet ROHF treatment of the ground state, for excitation energies only.
6.2.4 Spin-Flip Extended CIS (SF-XCIS)
Spin-flip extended CIS (SF-XCIS) [315] is a spin-complete extension of the spin-flip single excitation configuration interaction (SF-CIS) method [316]. The method includes all configurations in which no more than one virtual level of the high spin triplet reference becomes occupied and no more than one doubly occupied level becomes vacant.
SF-XCIS is defined only from a restricted open shell Hartree-Fock triplet ground state reference. The final SF-XCIS wavefunctions correspond to spin-pure  (singlet or triplet) states. The fully balanced treatment of the half-occupied reference orbitals makes it very suitable for applications with two strongly correlated electrons, such as single bond dissociation, systems with important diradical character or the study of excited states with significant double excitation character.
(singlet or triplet) states. The fully balanced treatment of the half-occupied reference orbitals makes it very suitable for applications with two strongly correlated electrons, such as single bond dissociation, systems with important diradical character or the study of excited states with significant double excitation character.
The computational cost of SF-XCIS scales in the same way with molecule size as CIS itself, with a pre-factor 13 times larger.
6.2.5 Basic Job Control Options
See also JOBTYPE, BASIS, EXCHANGE and CORRELATION. EXCHANGE must be HF and CORRELATION must be NONE. The minimum input required above a ground state HF calculation is to specify a nonzero value for CIS_N_ROOTS.
CIS_N_ROOTS
Sets the number of CI-Singles (CIS) excited state roots to find
TYPE:
INTEGER
DEFAULT:
0
Do not look for any excited states
OPTIONS:

Looks for
CIS excited states
RECOMMENDATION:
None
CIS_SINGLETS
Solve for singlet excited states in RCIS calculations (ignored for UCIS)
TYPE:
LOGICAL
DEFAULT:
TRUE
OPTIONS:
TRUE
Solve for singlet states
FALSE
Do not solve for singlet states.
RECOMMENDATION:
None
CIS_TRIPLETS
Solve for triplet excited states in RCIS calculations (ignored for UCIS)
TYPE:
LOGICAL
DEFAULT:
TRUE
OPTIONS:
TRUE
Solve for triplet states
FALSE
Do not solve for triplet states.
RECOMMENDATION:
None
RPA
Do an RPA calculation in addition to a CIS or TDDFT/TDA calculation
TYPE:
LOGICAL/INTEGER
DEFAULT:
False
OPTIONS:
False
Do not do an RPA calculation
True
Do an RPA calculation.
2
Do an RPA calculation without running CIS or TDDFT/TDA first
RECOMMENDATION:
None
SPIN_FLIP
Selects whether to perform a standard excited state calculation, or a spin-flip calculation. Spin multiplicity should be set to 3 for systems with an even number of electrons, and 4 for systems with an odd number of electrons.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
TRUE/FALSE
RECOMMENDATION:
None
SPIN_FLIP_XCIS
Do a SF-XCIS calculation
TYPE:
LOGICAL
DEFAULT:
False
OPTIONS:
False
Do not do an SF-XCIS calculation
True
Do an SF-XCIS calculation (requires ROHF triplet ground state).
RECOMMENDATION:
None
SFX_AMP_OCC_A
Defines a customer amplitude guess vector in SF-XCIS method
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:

builds a guess amplitude with an
-hole in the
th orbital (requires SFX_AMP_VIR_B).
RECOMMENDATION:
Only use when default guess is not satisfactory
SFX_AMP_VIR_B
Defines a customer amplitude guess vector in SF-XCIS method
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:

builds a guess amplitude with a
-particle in the
th orbital (requires SFX_AMP_OCC_A).
RECOMMENDATION:
Only use when default guess is not satisfactory
XCIS
Do an XCIS calculation in addition to a CIS calculation
TYPE:
LOGICAL
DEFAULT:
False
OPTIONS:
False
Do not do an XCIS calculation
True
Do an XCIS calculation (requires ROHF ground state).
RECOMMENDATION:
None
6.2.6 Customization
N_FROZEN_CORE
Controls the number of frozen core orbitals
TYPE:
INTEGER
DEFAULT:
0
No frozen core orbitals
OPTIONS:
FC
Frozen core approximation

Freeze
core orbitals
RECOMMENDATION:
There is no computational advantage to using frozen core for CIS, and analytical derivatives are only available when no orbitals are frozen. It is helpful when calculating CIS(D) corrections (see Sec. 6.6).
N_FROZEN_VIRTUAL
Controls the number of frozen virtual orbitals.
TYPE:
INTEGER
DEFAULT:
0
No frozen virtual orbitals
OPTIONS:

Freeze
virtual orbitals
RECOMMENDATION:
There is no computational advantage to using frozen virtuals for CIS, and analytical derivatives are only available when no orbitals are frozen.
MAX_CIS_CYCLES
Maximum number of CIS iterative cycles allowed
TYPE:
INTEGER
DEFAULT:
30
OPTIONS:

User-defined number of cycles
RECOMMENDATION:
Default is usually sufficient.
MAX_CIS_SUBSPACE
Maximum number of subspace vectors allowed in the CIS iterations
TYPE:
INTEGER
DEFAULT:
As many as required to converge all roots
OPTIONS:

User-defined number of subspace vectors
RECOMMENDATION:
The default is usually appropriate, unless a large number of states are requested for a large molecule. The total memory required to store the subspace vectors is bounded above by
, where
and
represent the number of occupied and virtual orbitals, respectively.
can be reduced to save memory, at the cost of a larger number of CIS iterations. Convergence may be impaired if
is not much larger than
.
CIS_CONVERGENCE
CIS is considered converged when error is less than
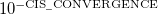
TYPE:
INTEGER
DEFAULT:
6
CIS convergence threshold 10
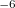
OPTIONS:

Corresponding to
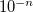
RECOMMENDATION:
None
CIS_DYNAMIC_MEM
Controls whether to use static or dynamic memory in CIS and TDDFT calculations.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Partly use static memory
TRUE
Fully use dynamic memory
RECOMMENDATION:
The default control requires static memory (MEM_STATIC) to hold a temporary array whose minimum size is
. For a large calculation, one has to specify a large value for MEM_STATIC, which is not recommended (see Chapter 2). Therefore, it is recommended to use dynamic memory for large calculations.
CIS_RELAXED_DENSITY
Use the relaxed CIS density for attachment/detachment density analysis
TYPE:
LOGICAL
DEFAULT:
False
OPTIONS:
False
Do not use the relaxed CIS density in analysis
True
Use the relaxed CIS density in analysis.
RECOMMENDATION:
None
CIS_GUESS_DISK
Read the CIS guess from disk (previous calculation)
TYPE:
LOGICAL
DEFAULT:
False
OPTIONS:
False
Create a new guess
True
Read the guess from disk
RECOMMENDATION:
Requires a guess from previous calculation.
CIS_GUESS_DISK_TYPE
Determines the type of guesses to be read from disk
TYPE:
INTEGER
DEFAULT:
Nil
OPTIONS:
0
Read triplets only
1
Read triplets and singlets
2
Read singlets only
RECOMMENDATION:
Must be specified if CIS_GUESS_DISK is TRUE.
STS_MOM
Control calculation of the transition moments between excited states in the CIS and TDDFT calculations (including SF-CIS and SF-DFT).
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE
Do not calculate state-to-state transition moments.
TRUE
Do calculate state-to-state transition moments.
RECOMMENDATION:
When set to true requests the state-to-state dipole transition moments for all pairs of excited states and for each excited state with the ground state.
Note: This option is not available for SF-XCIS.
CIS_MOMENTS
Controls calculation of excited-state (CIS or TDDFT) multipole moments
TYPE:
LOGICAL/INTEGER
DEFAULT:
FALSE
(or 0)
OPTIONS:
FALSE
(or 0) Do not calculate excited-state moments.
TRUE
(or 1) Calculate moments for each excited state.
RECOMMENDATION:
Set to TRUE if excited-state moments are desired. (This is a trivial additional calculation.) The MULTIPOLE_ORDER controls how many multipole moments are printed.
6.2.7 CIS Analytical Derivatives
While CIS excitation energies are relatively inaccurate, with errors of the order of 1 eV, CIS excited state properties, such as structures and frequencies, are much more useful. This is very similar to the manner in which ground state Hartree-Fock (HF) structures and frequencies are much more accurate than HF relative energies. Generally speaking, for low-lying excited states, it is expected that CIS vibrational frequencies will be systematically 10% higher or so relative to experiment [317, 318, 319]. If the excited states are of pure valence character, then basis set requirements are generally similar to the ground state. Excited states with partial Rydberg character require the addition of one or preferably two sets of diffuse functions.
Q-Chem includes efficient analytical first and second derivatives of the CIS energy [320, 321], to yield analytical gradients, excited state vibrational frequencies, force constants, polarizabilities, and infrared intensities. Their evaluation is controlled by two $rem variables, listed below. Analytical gradients can be evaluated for any job where the CIS excitation energy calculation itself is feasible.
JOBTYPE
Specifies the type of calculation
TYPE:
STRING
DEFAULT:
SP
OPTIONS:
SP
Single point energy
FORCE
Analytical Force calculation
OPT
Geometry Minimization
TS
Transition Structure Search
FREQ
Frequency Calculation
RECOMMENDATION:
None
CIS_STATE_DERIV
Sets CIS state for excited state optimizations and vibrational analysis
TYPE:
INTEGER
DEFAULT:
0
Does not select any of the excited states
OPTIONS:

Select the
th state.
RECOMMENDATION:
Check to see that the states do no change order during an optimization
The semi-direct method [313] used to evaluate the frequencies is generally similar to the semi-direct method used to evaluate Hartree-Fock frequencies for the ground state. Memory and disk requirements (see below) are similar, and the computer time scales approximately as the cube of the system size for large molecules.
The main complication associated with running analytical CIS second derivatives is ensuring Q-Chem has sufficient memory to perform the calculations. For most purposes, the defaults will be adequate, but if a large calculation fails due to a memory error, then the following additional information may be useful in fine tuning the input, and understanding why the job failed. Note that the analytical CIS second derivative code does not currently support frozen core or virtual orbitals (unlike Q-Chem’s MP2 code). Unlike MP2 calculations, applying frozen core/virtual orbital approximations does not lead to large computational savings in CIS calculations as all computationally expensive steps are performed in the atomic basis.
The memory requirements for CIS (and HF) analytical frequencies are primarily extracted from “C” memory, which is defined as
“C” memory must be large enough to contain a number of arrays whose size is 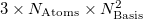 (
(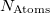 is the number of atoms and
is the number of atoms and 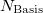 refers to the number of basis functions). The value of the $rem variable MEM_STATIC should be set sufficiently large to permit efficient integral evaluation. If too large, it reduces the amount of “C” memory available. If too small, the job may fail due to insufficient scratch space. For most purposes, a value of about 80 Mb is sufficient, and by default MEM_TOTAL is set to a very large number (larger than physical memory on most computers) and thus malloc (memory allocation) errors may occur on jobs where the memory demands exceeds physical memory.
refers to the number of basis functions). The value of the $rem variable MEM_STATIC should be set sufficiently large to permit efficient integral evaluation. If too large, it reduces the amount of “C” memory available. If too small, the job may fail due to insufficient scratch space. For most purposes, a value of about 80 Mb is sufficient, and by default MEM_TOTAL is set to a very large number (larger than physical memory on most computers) and thus malloc (memory allocation) errors may occur on jobs where the memory demands exceeds physical memory.
6.2.8 Examples
Example 6.107 A basic CIS excitation energy calculation on formaldehyde at the HF/6-31G* optimized ground state geometry, which is obtained in the first part of the job. Above the first singlet excited state, the states have Rydberg character, and therefore a basis with two sets of diffuse functions is used.
$molecule
0 1
C
O 1 CO
H 1 CH 2 A
H 1 CH 2 A 3 D
CO = 1.2
CH = 1.0
A = 120.0
D = 180.0
$end
$rem
jobtype = opt
exchange = hf
basis = 6-31G*
$end
@@@
$molecule
read
$end
$rem
exchange = hf
basis = 6-311(2+)G*
cis_n_roots = 15 Do 15 states
cis_singlets = true Do do singlets
cis_triplets = false Don't do Triplets
$end
Example 6.108 An XCIS calculation of excited states of an unsaturated radical, the phenyl radical, for which double substitutions make considerable contributions to low-lying excited states.
$comment
C6H5 phenyl radical C2v symmetry MP2(full)/6-31G* = -230.7777459
$end
$molecule
0 2
c1
x1 c1 1.0
c2 c1 rc2 x1 90.0
x2 c2 1.0 c1 90.0 x1 0.0
c3 c1 rc3 x1 90.0 c2 tc3
c4 c1 rc3 x1 90.0 c2 -tc3
c5 c3 rc5 c1 ac5 x1 -90.0
c6 c4 rc5 c1 ac5 x1 90.0
h1 c2 rh1 x2 90.0 c1 180.0
h2 c3 rh2 c1 ah2 x1 90.0
h3 c4 rh2 c1 ah2 x1 -90.0
h4 c5 rh4 c3 ah4 c1 180.0
h5 c6 rh4 c4 ah4 c1 180.0
rh1 = 1.08574
rh2 = 1.08534
rc2 = 2.67299
rc3 = 1.35450
rh4 = 1.08722
rc5 = 1.37290
tc3 = 62.85
ah2 = 122.16
ah4 = 119.52
ac5 = 116.45
$end
$rem
basis = 6-31+G*
exchange = hf
mem_static = 80
intsbuffersize = 15000000
scf_convergence = 8
cis_n_roots = 5
xcis = true
$end
Example 6.109 A SF-XCIS calculation of ground and excited states of trimethylenemethane (TMM) diradical, for which double substitutions make considerable contributions to low-lying exc ited states.
$comment
TMM ground and excited states
$end
$molecule
0 3
C
C 1 CC1
C 1 CC2 2 A2
C 1 CC2 2 A2 3 180.0
H 2 C2H 1 C2CH 3 0.0
H 2 C2H 1 C2CH 4 0.0
H 3 C3Hu 1 C3CHu 2 0.0
H 3 C3Hd 1 C3CHd 4 0.0
H 4 C3Hu 1 C3CHu 2 0.0
H 4 C3Hd 1 C3CHd 3 0.0
CC1 = 1.35
CC2 = 1.47
C2H = 1.083
C3Hu = 1.08
C3Hd = 1.08
C2CH = 121.2
C3CHu = 120.3
C3CHd = 121.3
A2 = 121.0
$end
$rem
unrestricted = false SF-XCIS runs from ROHF triplet reference
exchange = HF
basis = 6-31G*
scf_convergence = 10
scf_algorithm = DM
max_scf_cycles = 100
spin_flip_xcis = true Do SF-XCIS
cis_n_roots = 3
cis_singlets = true Do singlets
cis_triplets = true Do triplets
$end
Example 6.110 This example illustrates a CIS geometry optimization followed by a vibrational frequency analysis on the lowest singlet excited state of formaldehyde. This 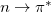 excited state is non-planar, unlike the ground state. The optimization converges to a non-planar structure with zero forces, and all frequencies real.
excited state is non-planar, unlike the ground state. The optimization converges to a non-planar structure with zero forces, and all frequencies real.
$comment
singlet n -> pi* state optimization and frequencies for formaldehyde
$end
$molecule
0 1
C
O 1 CO
H 1 CH 2 A
H 1 CH 2 A 3 D
CO = 1.2
CH = 1.0
A = 120.0
D = 150.0
$end
$rem
jobtype = opt
exchange = hf
basis = 6-31+G*
cis_state_deriv = 1 Optimize state 1
cis_n_roots = 3 Do 3 states
cis_singlets = true Do do singlets
cis_triplets = false Don't do Triplets
$end
@@@
$molecule
read
$end
$rem
jobtype = freq
exchange = hf
basis = 6-31+G*
cis_state_deriv = 1 Focus on state 1
cis_n_roots = 3 Do 3 states
cis_singlets = true Do do singlets
cis_triplets = false Don't do Triplets
$end
6.2.9 Non-Orthogonal Configuration Interaction
Some systems such as transition metals, open-shell species, and dissociating molecules feature multiple closely lying solutions to the SCF equations. By using SCF Metadynamics (see Chapter 4), these can be successfully located, however, there is no clear physical reason to choose one SCF solution over another, rather, it is appropriate to have a method that treats these solutions on an equal footing. In particular, these SCF solutions are not subject to non-crossing rules, and do in fact often cross each other as geometry is changed, so the lowest energy state may switch abruptly with consequent discontinuities in the energy gradients. To achieve a smoother, more qualitatively correct surface, these SCF solutions can be used as a basis for a Configuration Interaction calculation, where the resultant wavefunction will either smoothly interpolate between these states. As the SCF states are not orthogonal to each other (one cannot be constructed as a single determinant made out of the orbitals of another), and so the CI is a little more complicated and denoted Non-Orthogonal Configuration Interaction (NOCI) [322].
This can be viewed as an alternative to CASSCF within an “active space” of SCF states of interest, and has the advantage that the SCF states, and thus the NOCI wavefunctions are size-consistent. In common with CASSCF, it is able to describe complicated phenomena such as avoided crossings (where states mix instead of passing through each other), and conical intersections (where through symmetry or accidental reasons, there is no coupling between the states, and they pass cleanly through each other at a degeneracy).
Another use for a NOCI calculation is that of symmetry purification. At some geometries, the SCF states break spatial or spin symmetry to achieve a lower energy single determinant than if these symmetries were conserved. As these symmetries still exist within the Hamiltonian, its true eigenfunctions will preserve these symmetries. In the case of spin, this manifests itself as spin-contamination, and for spatial symmetries, the orbitals will usually adopt a more localized structure. To recover a (yet lower energy) wavefunction retaining the correct symmetries, one can include these symmetry broken states (with all relevant symmetry permutations) in a NOCI calculation, and the resultant eigenfunction will have the true symmetries restored as a linear combination of these broken symmetry states. A common example would be for a UHF state which has an indefinite spin (value of 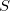 not
not 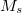 ). By including a UHF solution along with its spin-flipped version (where all alpha and beta orbitals have been switched) in NOCI, the resultant wavefunction will be a more pure spin state (though there is still no guarantee of finding an eigenfunction of
). By including a UHF solution along with its spin-flipped version (where all alpha and beta orbitals have been switched) in NOCI, the resultant wavefunction will be a more pure spin state (though there is still no guarantee of finding an eigenfunction of 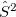 ), reducing spin contamination in the same way as the Half-Projected Hartree-Fock method [323]. As an example using an
), reducing spin contamination in the same way as the Half-Projected Hartree-Fock method [323]. As an example using an 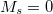 UHF wavefunction and its spin-flipped version will produce two new NOCI eigenfunctions, one with even
UHF wavefunction and its spin-flipped version will produce two new NOCI eigenfunctions, one with even 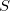 (a mixture of
(a mixture of 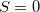 ,
, 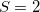 , …), and one with odd (mixing
, …), and one with odd (mixing 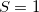 ,
, 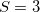 ,…), which may be use as approximations to singlet and triplet wavefunctions.
,…), which may be use as approximations to singlet and triplet wavefunctions.
NOCI can be enabled by specifying CORRELATION NOCI, and will automatically use all of the states located with SCF metadynamics. To merely include the two spin-flipped versions of a UHF wavefunction, this can be specified without turning metadynamics on. For more customization, a $noci section can be included in the input file to specify the states to include:
Example 6.111 $noci section example
This section specifies (first line) that states 1,2, and 4 are to be included as well as the spin-flipped version of state 2 (the -2 indicates this). The second line (optional) indicates which (zero-based) eigenvalue is to be returned to Q-Chem (the third in this case). Analytic gradients are not available for NOCI, but finite difference geometry optimizers are available.
$noci
1 2 -2 4
2
$end
NOCI_PRINT
Specify the debug print level of NOCI
TYPE:
INTEGER
DEFAULT:
1
OPTIONS:
RECOMMENDATION:
Increase this for more debug information