Q-Chem 4.3 User’s Manual

10.13 Anharmonic Vibrational Frequencies

Computing vibrational spectra beyond the harmonic approximation has become an active area of research owing to the improved efficiency of computer techniques [514, 515, 516, 517]. To calculate the exact vibrational spectrum within Born-Oppenheimer approximation, one has to solve the nuclear Schrödinger equation completely using numerical integration techniques, and consider the full configuration interaction of quanta in the vibrational states. This has only been carried out on di- or triatomic system [518, 519]. The difficulty of this numerical integration arises because solving exact the nuclear Schrödinger equation requires a complete electronic basis set, consideration of all the nuclear vibrational configuration states, and a complete potential energy surface (PES). Simplification of the Nuclear Vibration Theory (NVT) and PES are the doorways to accelerating the anharmonic correction calculations. There are five aspects to simplifying the problem:

To incorporate these simplifications, new formulae combining information from the Hessian, gradient and energy are used as a default procedure to calculate the cubic and quartic force field of a given potential energy surface.

Here, we also briefly describe various NVT methods. In the early stage of solving the nuclear Schrödinger equation (in the 1930s), second-order Vibrational Perturbation Theory (VPT2) was developed [520, 521, 522, 523, 517]. However, problems occur when resonances exist in the spectrum. This becomes more problematic for larger molecules due to the greater chance of accidental degeneracies occurring. To avoid this problem, one can do a direct integration of the secular matrix using Vibrational Configuration Interaction (VCI) theory [524]. It is the most accurate method and also the least favored due to its computational expense. In Q-Chem 3.0, we introduce a new approach to treating the wavefunction, transition-optimized shifted Hermite (TOSH) theory [525], which uses first-order perturbation theory, which avoids the degeneracy problems of VPT2, but which incorporates anharmonic effects into the wavefunction, thus increasing the accuracy of the predicted anharmonic energies.

10.13.1 Partial Hessian Vibrational Analysis

The computation of harmonic frequencies for systems with a very large number of atoms can become computationally expensive. However, in many cases only a few specific vibrational modes or vibrational modes localized in a region of the system are of interest. A typical example is the calculation of the vibrational modes of a molecule adsorbed on a surface. In such a case, only the vibrational modes of the adsorbate are useful, and the vibrational modes associated with the surface atoms are of less interest. If the vibrational modes of interest are only weakly coupled to the vibrational modes associated with the rest of the system, it can be appropriate to adopt a partial Hessian approach. In this approach [526, 527], only the part of the Hessian matrix comprising the second derivatives of a subset of the atoms defined by the user is computed. These atoms are defined in the $alist block. This results in a significant decrease in the cost of the calculation. Physically, this approximation corresponds to assigning an infinite mass to all the atoms excluded from the Hessian and will only yield sensible results if these atoms are not involved in the vibrational modes of interest. VPT2 and TOSH anharmonic frequencies can be computed following a partial Hessian calculation [528]. It is also possible to include a subset of the harmonic vibrational modes with an anharmonic frequency calculation by invoking the ANHAR_SEL rem. This can be useful to reduce the computational cost of an anharmonic frequency calculation or to explore the coupling between specific vibrational modes.

Alternatively, vibrationally averaged interactions with the rest of the system can be folded into a partial Hessian calculation using vibrational subsystem analysis [529, 530]. Based on an adiabatic approximation, this procedure reduces the cost of diagonalizing the full Hessian, while providing a local probe of fragments vibrations, and providing better than partial Hessian accuracy for the low frequency modes of large molecules [531]. Mass-effects from the rest of the system can be vibrationally averaged or excluded within this scheme.

PHESS

Controls whether partial Hessian calculations are performed.


TYPE:

INTEGER


DEFAULT:

0

Full Hessian calculation


OPTIONS:

0

Full Hessian calculation

1

Partial Hessian calculation

2

Vibrational subsystem analysis (massless)

3

Vibrational subsystem analysis (weighted)


RECOMMENDATION:

None


N_SOL

Specifies number of atoms included in the Hessian


TYPE:

INTEGER


DEFAULT:

No default


OPTIONS:

User defined


RECOMMENDATION:

None


PH_FAST

Lowers integral cutoff in partial Hessian calculation is performed.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use default cutoffs


OPTIONS:

TRUE

Lower integral cutoffs


RECOMMENDATION:

None


ANHAR_SEL

Select a subset of normal modes for subsequent anharmonic frequency analysis.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use all normal modes


OPTIONS:

TRUE

Select subset of normal modes


RECOMMENDATION:

None


Example 10.223  This example shows a partial Hessian frequency calculation of the vibrational frequencies of acetylene on a model of the C(100) surface

$comment
   acetylene - C(100)
   partial Hessian calculation
$end

$molecule
0 1
   C  0.000  0.659 -2.173
   C  0.000 -0.659 -2.173
   H  0.000  1.406 -2.956
   H  0.000 -1.406 -2.956
   C  0.000  0.786 -0.647
   C  0.000 -0.786 -0.647
   C  1.253  1.192  0.164
   C -1.253  1.192  0.164
   C  1.253 -1.192  0.164
   C  1.297  0.000  1.155
   C -1.253 -1.192  0.164
   C  0.000  0.000  2.023
   C -1.297  0.000  1.155
   H -2.179  0.000  1.795
   H -1.148 -2.156  0.654
   H  0.000 -0.876  2.669
   H  2.179  0.000  1.795
   H -1.148  2.156  0.654
   H -2.153 -1.211 -0.446
   H  2.153 -1.211 -0.446
   H  1.148 -2.156  0.654
   H  1.148  2.156  0.654
   H  2.153  1.211 -0.446
   H -2.153  1.211 -0.446
   H  0.000  0.876  2.669
$end

$rem
   JOBTYPE           freq
   METHOD            hf
   BASIS             sto-3g
   PHESS             TRUE
   N_SOL             4
$end

$alist
1
2
3
4
$end

Example 10.224  This example shows an anharmonic frequency calculation for ethene where only the C-H stretching modes are included in the anharmonic analysis.

$comment
  ethene
  restricted anharmonic frequency analysis
$end

$molecule
0 1
  C   0.6665   0.0000   0.0000
  C  -0.6665   0.0000   0.0000
  H   1.2480   0.9304   0.0000
  H  -1.2480  -0.9304   0.0000
  H  -1.2480   0.9304   0.0000
  H   1.2480  -0.9304   0.0000
$end

$rem
   JOBTYPE           freq
   METHOD            hf
   BASIS             sto-3g
   ANHAR_SEL         TRUE
   N_SOL             4
$end

$alist
9
10
11
12
$end

10.13.2 Vibration Configuration Interaction Theory

To solve the nuclear vibrational Schrödinger equation, one can only use direct integration procedures for diatomic molecules [518, 519]. For larger systems, a truncated version of full configuration interaction is considered to be the most accurate approach. When one applies the variational principle to the vibrational problem, a basis function for the nuclear wavefunction of the $n$th excited state of mode $i$ is

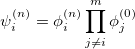  \begin{equation} \label{eq:bas} \psi ^{(n)}_ i =\phi ^{(n)}_{i} \prod ^{m}_{j\neq i} \phi ^{(0)}_{j} \end{equation}   (10.43)

where the 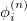$\phi _ i^{(n)}$ represents the harmonic oscillator eigenfunctions for normal mode 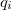$q_ i$. This can be expressed in terms of Hermite polynomials:

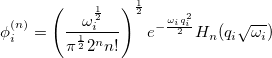  \begin{equation} \label{eq:wavefunction} {\phi }^{(n)}_ i = \left(\frac{\omega _ i ^{\frac{1}{2}}}{{\pi }^{\frac{1}{2}}2^ nn!} \right)^{\frac{1}{2}} {e^{- \frac{\omega _ i q_ i^2}{2}}} H_ n( q_ i{\sqrt {\omega _ i }}) \end{equation}   (10.44)

With the basis function defined in Eq. (10.43), the $n$th wavefunction can be described as a linear combination of the Hermite polynomials:

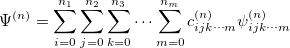  \begin{equation} \Psi ^{(n)} = \sum _{i=0}^{n_1}\sum _{j=0}^{n_2}\sum _{k=0}^{n_3}\cdots \sum _{m=0}^{n_ m}c^{(n)}_{ijk\cdots m}\psi _{ijk\cdots m}^{(n)} \end{equation}   (10.45)

where 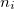$n_ i$ is the number of quanta in the $i$th mode. We propose the notation VCI(n) where $n$ is the total number of quanta, i.e.:

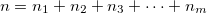  \begin{equation} n = n_1 + n_2 + n_3 + \cdots + n_ m \end{equation}   (10.46)

To determine this expansion coefficient 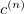$c^{(n)}$, we integrate the 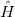$\hat{H}$, as in Eq. (4.1), with 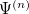$\Psi ^{(n)}$ to get the eigenvalues

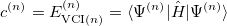  \begin{equation} \label{eq:VCI} c^{(n)} = E^{(n)}_{\ensuremath{\mathrm{VCI}}(n)} = \langle \Psi ^{(n)} | \hat{H} | \Psi ^{(n)} \rangle \end{equation}   (10.47)

This gives us frequencies that are corrected for anharmonicity to $n$ quanta accuracy for a 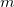$m$-mode molecule. The size of the secular matrix on the right hand of Eq. (10.47) is 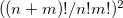$((n+m)!/n!m!)^2$, and the storage of this matrix can easily surpass the memory limit of a computer. Although this method is highly accurate, we need to seek for other approximations for computing large molecules.

10.13.3 Vibrational Perturbation Theory

Vibrational perturbation theory has been historically popular for calculating molecular spectroscopy. Nevertheless, it is notorious for the inability of dealing with resonance cases. In addition, the non-standard formulas for various symmetries of molecules forces the users to modify inputs on a case-by-case basis [532, 533, 534], which narrows the accessibility of this method. VPT applies perturbation treatments on the same Hamiltonian as in Eq. (4.1), but divides it into an unperturbed part, 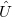$\hat{U}$,

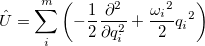  \begin{equation} \hat{U} = \sum _{i}^{m} \left( -\frac{1}{2} \frac{\partial ^2}{\partial q_ i^2} + \frac{{{{\omega }_ i}}^2}{2}{{q_ i}}^2 \right) \end{equation}   (10.48)

and a perturbed part, 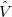$\hat{V}$:

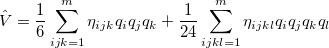  \begin{equation} \hat{V} = \frac{1}{6} \sum _{{ijk} = 1}^{m} {{\eta }_{{ijk}}}{q_ i}{q_ j}{q_ k} + \frac{1}{24} \sum _{{ijkl} = 1}^{m} {{\eta }_{{ijkl}}}{q_ i}{q_ j} {q_ k}{q_ l} \end{equation}   (10.49)

One can then apply second-order perturbation theory to get the $i$th excited state energy:

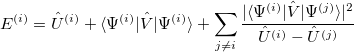  \begin{equation} \label{eq:VPT2} E^{(i)} = \hat{U}^{(i)} + \langle \Psi ^{(i)} | \hat{V} | \Psi ^{(i)} \rangle + \sum _{j\neq i } \frac{|\langle \Psi ^{(i)}|\hat{V}|\Psi ^{(j)}\rangle |^2}{ \hat{U}^{(i)} - \hat{U}^{(j)}} \end{equation}   (10.50)

The denominator in Eq. (10.50) can be zero either because of symmetry or accidental degeneracy. Various solutions, which depend on the type of degeneracy that occurs, have been developed which ignore the zero-denominator elements from the Hamiltonian [535, 532, 533, 534]. An alternative solution has been proposed by Barone [517] which can be applied to all molecules by changing the masses of one or more nuclei in degenerate cases. The disadvantage of this method is that it will break the degeneracy which results in fundamental frequencies no longer retaining their correct symmetry. He proposed

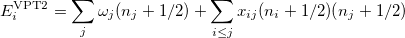  \begin{equation} E_ i^{\ensuremath{\mathrm{VPT2}}} = \sum _ j \omega _ j (n_ j+1/2) + \sum _{i\leq j} x_{ij} (n_ i+1/2)(n_ j+1/2) \end{equation}   (10.51)

where, if rotational coupling is ignored, the anharmonic constants 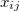$x_{ij}$ are given by

  \begin{equation} x_{ij} = \frac{1}{4\omega _ i\omega _ j} \left( \eta _{iijj} - \sum _ k^ m \frac{\eta _{iik}\eta _{jjk}}{\omega _ k^2} + \sum _ k^ m \frac{2(\omega _ i^2+\omega _ j^2-\omega _ k^2)\eta _{ijk}^2}{ \left[(\omega _ i+\omega _ j)^2-\omega _ k^2\right] \left[(\omega _ i-\omega _ j)^2-\omega _ k^2\right]}\right) \end{equation}   (10.52)

10.13.4 Transition-Optimized Shifted Hermite Theory

So far, every aspect of solving the nuclear wave equation has been considered, except the wavefunction. Since Schrödinger proposed his equation, the nuclear wavefunction has traditionally be expressed in terms of Hermite functions, which are designed for the harmonic oscillator case. Recently [525], a modified representation has been presented. To demonstrate how this approximation works, we start with a simple example. For a diatomic molecule, the Hamiltonian with up to quartic derivatives can be written as

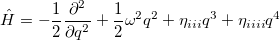  \begin{equation} \hat{H} = - \frac{1}{2} \frac{\partial ^2}{\partial q^2} + \frac{1}{2}{\omega }^2q^2 + \eta _{iii} q^3 + \eta _{iiii} q^4 \end{equation}   (10.53)

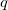and the wavefunction is expressed as in Eq. (10.44). Now, if we shift the center of the wavefunction by $\sigma $, which is equivalent to a translation of the normal coordinate $q$, the shape will still remain the same, but the anharmonic correction can now be incorporated into the wavefunction. For a ground vibrational state, the wavefunction is written as

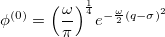  \begin{equation} \phi ^{(0)} = {\left( \frac{\omega }{\pi } \right) }^{\frac{1}{4}} e^{ -\frac{\omega }{2} {\left( q - \sigma \right) }^2} \end{equation}   (10.54)

Similarly, for the first excited vibrational state, we have

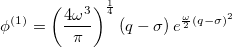  \begin{equation} \phi ^{(1)} = {\left( \frac{4{\omega }^3}{\pi } \right) }^{\frac{1}{4}} \left( q - \sigma \right) e^{\frac{\omega }{2}{\left( q - \sigma \right) }^2} \end{equation}   (10.55)

Therefore, the energy difference between the first vibrational excited state and the ground state is

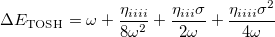  \begin{equation} \label{eq:di-TOSH} \Delta E_{\ensuremath{\mathrm{TOSH}}}= \omega + \frac{\eta _{iiii} }{8{\omega }^2} + \frac{\eta _{iii} \sigma }{2\omega } + \frac{\eta _{iiii} {\sigma }^2}{4\omega } \end{equation}   (10.56)

This is the fundamental vibrational frequency from first-order perturbation theory.

Meanwhile, We know from the first-order perturbation theory with an ordinary wavefunction within a QFF PES, the energy is

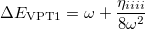  \begin{equation} \Delta E_{\ensuremath{\mathrm{VPT}}1} = \omega + \frac{\eta _{iiii} }{8{\omega }^2} \end{equation}   (10.57)

The differences between these two wavefunctions are the two extra terms arising from the shift in Eq. (10.56). To determine the shift, we compare the energy with that from second-order perturbation theory:

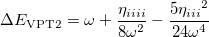  \begin{equation} \Delta E_{\ensuremath{\mathrm{VPT}}2} = \omega + \frac{\eta _{iiii} }{8{\omega }^2} - \frac{5{\eta _{iii} }^2}{24{\omega }^4} \end{equation}   (10.58)

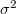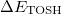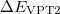Since $\sigma $ is a very small quantity compared with the other variables, we ignore the contribution of $\sigma ^2$ and compare $\Delta E_{\ensuremath{\mathrm{TOSH}}}$ with $\Delta E_{\ensuremath{\mathrm{VPT}}2}$, which yields an initial guess for $\sigma $:

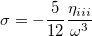  \begin{equation} \sigma = -\frac{5}{12} \frac{\eta _{iii}}{\omega ^3} \end{equation}   (10.59)

Because the only difference between this approach and the ordinary wavefunction is the shift in the normal coordinate, we call it “transition-optimized shifted Hermite” (TOSH) functions [525]. This approximation gives second-order accuracy at only first-order cost.

For polyatomic molecules, we consider Eq. (10.56), and propose that the energy of the $i$th mode be expressed as:

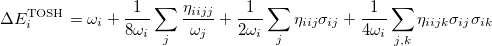  \begin{equation} \Delta E_{i}^{\ensuremath{\mathrm{TOSH}}} = \omega _ i + \frac{1}{8\omega _ i} \sum _ j \frac{\eta _{iijj}}{\omega _ j} + \frac{1}{2\omega _ i} \sum _ j \eta _{iij} \sigma _{ij} + \frac{1}{4\omega _ i} \sum _{j,k} \eta _{iijk}\sigma _{ij}\sigma _{ik} \end{equation}   (10.60)

Following the same approach as for the diatomic case, by comparing this with the energy from second-order perturbation theory, we obtain the shift as

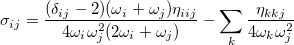  \begin{equation} \sigma _{ij} = \frac{(\delta _{ij}-2)(\omega _ i+\omega _ j)\eta _{iij}}{ 4\omega _ i \omega _ j^2(2\omega _ i+\omega _ j)} - \sum _ k \frac{\eta _{kkj}}{4\omega _ k\omega _ j^2} \end{equation}   (10.61)

10.13.5 Job Control

The following $rem variables can be used to control the calculation of anharmonic frequencies.

ANHAR

Performing various nuclear vibrational theory (TOSH, VPT2, VCI) calculations to obtain vibrational anharmonic frequencies.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

TRUE

Carry out the anharmonic frequency calculation.

FALSE

Do harmonic frequency calculation.


RECOMMENDATION:

Since this calculation involves the third and fourth derivatives at the minimum of the potential energy surface, it is recommended that the GEOM_OPT_TOL_DISPLACEMENT, GEOM_OPT_TOL_GRADIENT and GEOM_OPT_TOL_ENERGY tolerances are set tighter. Note that VPT2 calculations may fail if the system involves accidental degenerate resonances. See the VCI $rem variable for more details about increasing the accuracy of anharmonic calculations.


VCI

Specifies the number of quanta involved in the VCI calculation.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

User-defined. Maximum value is 10.


RECOMMENDATION:

The availability depends on the memory of the machine. Memory allocation for VCI calculation is the square of $2*(N_\mathrm {Vib}+N_\mathrm {VCI})/N_\mathrm {Vib}N_\mathrm {VCI}$ with double precision. For example, a machine with 1.5 GB memory and for molecules with fewer than 4 atoms, VCI(10) can be carried out, for molecule containing fewer than 5 atoms, VCI(6) can be carried out, for molecule containing fewer than 6 atoms, VCI(5) can be carried out. For molecules containing fewer than 50 atoms, VCI(2) is available. VCI(1) and VCI(3) usually overestimated the true energy while VCI(4) usually gives an answer close to the converged energy.


FDIFF_DER

Controls what types of information are used to compute higher derivatives. The default uses a combination of energy, gradient and Hessian information, which makes the force field calculation faster.


TYPE:

INTEGER


DEFAULT:

3

for jobs where analytical 2nd derivatives are available.

0

for jobs with ECP.


OPTIONS:

0

Use energy information only.

1

Use gradient information only.

2

Use Hessian information only.

3

Use energy, gradient, and Hessian information.


RECOMMENDATION:

When the molecule is larger than benzene with small basis set, FDIFF_DER=2 may be faster. Note that FDIFF_DER will be set lower if analytic derivatives of the requested order are not available. Please refers to IDERIV.


MODE_COUPLING

Number of modes coupling in the third and fourth derivatives calculation.


TYPE:

INTEGER


DEFAULT:

2

for two modes coupling.


OPTIONS:

$n$

for $n$ modes coupling, Maximum value is 4.


RECOMMENDATION:

Use default.


IGNORE_LOW_FREQ

Low frequencies that should be treated as rotation can be ignored during

anharmonic correction calculation.


TYPE:

INTEGER


DEFAULT:

300

Corresponding to 300 cm$^{-1}$.


OPTIONS:

$n$

Any mode with harmonic frequency less than $n$ will be ignored.


RECOMMENDATION:

Use default.


FDIFF_STEPSIZE_QFF

Displacement used for calculating third and fourth derivatives by finite difference.


TYPE:

INTEGER


DEFAULT:

5291

Corresponding to 0.1 bohr. For calculating third and fourth derivatives.


OPTIONS:

$n$

Use a step size of $n\times 10^{-5}$.


RECOMMENDATION:

Use default, unless on a very flat potential, in which case a larger value should be used.


Example 10.225  A four-quanta anharmonic frequency calculation on formaldehyde at the EDF2/6-31G* optimized ground state geometry, which is obtained in the first part of the job. It is necessary to carry out the harmonic frequency first and this will print out an approximate time for the subsequent anharmonic frequency calculation. If a FREQ job has already been performed, the anharmonic calculation can be restarted using the saved scratch files from the harmonic calculation.

$molecule
   0 1
   C
   O, 1, CO
   H, 1, CH, 2, A
   H, 1, CH, 2, A, 3, D

   CO = 1.2
   CH = 1.0
   A  = 120.0
   D  = 180.0
$end
$rem
    JOBTYPE                     OPT
    METHOD                      EDF2
    BASIS                       6-31G*
    GEOM_OPT_TOL_DISPLACEMENT   1
    GEOM_OPT_TOL_GRADIENT       1
    GEOM_OPT_TOL_ENERGY         1 
$end
@@@
$molecule
    READ
$end
$rem
    JOBTYPE                     FREQ
    METHOD                      EDF2
    BASIS                       6-31G*
    ANHAR                       TRUE
    VCI                         4
$end

10.13.6 Isotopic Substitutions

By default Q-Chem calculates vibrational frequencies using the atomic masses of the most abundant isotopes (taken from the Handbook of Chemistry and Physics, $63^{\ensuremath{\mathrm{rd}}}$ Edition). Masses of other isotopes can be specified using the $isotopes section and by setting the ISOTOPES $rem variable to TRUE. The format of the $isotopes section is as follows: 

$isotopes
   number_of_isotope_loops  tp_flag
   number_of_atoms  [temp pressure] (loop 1)
   atom_number1   mass1
   atom_number2   mass2
   ...
   number_of_atoms  [temp pressure] (loop 2)
   atom_number1   mass1
   atom_number2   mass2
   ...
$end

Note: Only the atoms whose masses are to be changed from the default values need to be specified. After each loop all masses are reset to the default values. Atoms are numbered according to the order in the $molecule section.

An initial loop using the default masses is always performed first. Subsequent loops use the user-specified atomic masses. Only those atoms whose masses are to be changed need to be included in the list, all other atoms will adopt the default masses. The output gives a full frequency analysis for each loop. Note that the calculation of vibrational frequencies in the additional loops only involves a rescaling of the computed Hessian, and therefore takes little additional computational time.

The first line of the $isotopes section specifies the number of substitution loops and also whether the temperature and pressure should be modified. The tp_flag setting should be set to 0 if the default temperature and pressure are to be used (298.18 K and 1 atm respectively), or 1 if they are to be altered. Note that the temperatures should be specified in Kelvin (K) and pressures in atmospheres (atm).

ISOTOPES

Specifies if non-default masses are to be used in the frequency calculation.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Use default masses only.

TRUE

Read isotope masses from $isotopes section.


RECOMMENDATION:

None


Example 10.226  An EDF1/6-31+G* optimization, followed by a vibrational analysis. Doing the vibrational analysis at a stationary point is necessary for the results to be valid.

$molecule
   0  1
   C   1.08900   0.00000   0.00000
   C  -1.08900   0.00000   0.00000
   H   2.08900   0.00000   0.00000
   H  -2.08900   0.00000   0.00000
$end

$rem
   BASIS         3-21G
   JOBTYPE       opt
   METHOD        hf
$end

@@@

$molecule
   read
$end

$rem
   BASIS         3-21G
   JOBTYPE       freq
   METHOD        hf
   SCF_GUESS     read
   ISOTOPES      1
$end

$isotopes
   2   0           ! two loops, both at std temp and pressure
   4
     1   13.00336  ! All atoms are given non-default masses
     2   13.00336
     3   2.01410
     4   2.01410
   2 
     3   2.01410   ! H's replaced with D's
     4   2.01410
$end