6.1 General Excited-State Features
As for ground state calculations, performing an adequate excited-state calculation involves making an appropriate choice of method and basis set. The development of effective approaches to modeling electronic excited states has historically lagged behind advances in treating the ground state. In part this is because of the much greater diversity in the character of the wavefunctions for excited states, making it more difficult to develop broadly applicable methods without molecule-specific or even state-specific specification of the form of the wavefunction. Recently, however, a hierarchy of single-reference ab initio methods has begun to emerge for the treatment of excited states. Broadly speaking, Q-Chem contains methods that are capable of giving qualitative agreement, and in many cases quantitative agreement with experiment for lower optically allowed states. The situation is less satisfactory for states that involve two-electron excitations, although even here reasonable results can sometimes be obtained. Moreover, some of the excited state methods can treat open-shell wavefunctions, e.g. diradicals, ionized and electron attachment states and more.
In excited-state calculations, as for ground state calculations, the user must strike a compromise between cost and accuracy. The few sections of this Chapter summarize Q-Chem’s capabilities in four general classes of excited state methods:
Single-electron wavefunction-based methods (Section 6.2). These are excited state treatments of roughly the same level of sophistication as the Hartree-Fock ground state method, in the sense that electron correlation is essentially ignored. Single excitation configuration interaction (CIS) is the workhorse method of this type. The spin-flip variant of CIS extends it to diradicals.
Time-dependent density functional theory (TDDFT) (Section 6.3). TDDFT is the most useful extension of density functional theory to excited states that has been developed so far. For a cost that is little greater than the simple wavefunction methods such as CIS, a significantly more accurate method results. TDDFT can be extended to treat di- and tri-radicals and bond-breaking by adopting the spin-flip approach (see Section 6.3.1 for details).
The Maximum Overlap Method (MOM) for excited SCF states (Section 6.4). This method overcomes some of the deficiencies of TDDFT and, in particular, can be used for modeling charge-transfer and Rydberg transitions.
Restricted open-shell Kohn-Sham (ROKS) method is another
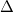-SCF approach for excited states (Section 6.5). Wavefunction-based electron correlation treatments (Sections 6.6, 6.8, 6.9 and 6.7). Roughly speaking, these are excited state analogs of the ground state wavefunction-based electron correlation methods discussed in Chapter 5. They are more accurate than the methods of Section 6.2, but also significantly more computationally expensive. These methods can also describe certain multi-configurational wavefunctions, for example, problematic doublet radicals, diradicals, triradicals, and more.
In general, a basis set appropriate for a ground state density functional theory or a Hartree-Fock calculation will be appropriate for describing valence excited states. However, many excited states involve significant contributions from diffuse Rydberg orbitals, and, therefore, it is often advisable to use basis sets that include additional diffuse functions. The 6-31+G* basis set is a reasonable compromise for the low-lying valence excited states of many organic molecules. To describe true Rydberg excited states, Q-Chem allows the user to add two or more sets of diffuse functions (see Chapter 7). For example the 6-311(2+)G* basis includes two sets of diffuse functions on heavy atoms and is generally adequate for description of both valence and Rydberg excited states.
Q-Chem supports four main types of excited state calculation:
Vertical absorption spectrum
This is the calculation of the excited states of the molecule at the ground state geometry, as appropriate for absorption spectroscopy. The methods supported for performing a vertical absorption calculation are: CIS, RPA, XCIS, SF-XCIS, CIS(D), ADC(2)-s, ADC(2)-x, ADC(3), RAS-SF, EOM-CCSD and EOM-OD, each of which will be discussed in turn.Visualization
It is possible to visualize the excited states either by attachment/detachment density analysis (available for CIS, RPA, TDDFT, and ADC only) or by plotting the transition density (see $plots descriptions in Chapters 3 and 10). Transition densities can be calculated for CIS, EOM-CCSD, and ADC methods. The theoretical basis of the attachment/detachment density analysis is discussed in Section 6.11.1 of this Chapter. In addition Dyson orbitals can be calculated and plotted for the ionization from the ground and electronically excited states for the CCSD and EOM-CCSD wavefunctions. For the RAS-SF method (Section 6.9), one can plot the natural orbitals of a computed electronic state.Excited-state optimization
Optimization of the geometry of stationary points on excited state potential energy surfaces is valuable for understanding the geometric relaxation that occurs between the ground and excited state. Analytic first derivatives are available for UCIS, RCIS, TDDFT and EOM-CCSD, EOM-OD excited state optimizations may also be performed using finite difference methods, however, these can be very time-consuming to compute.Optimization of the crossings between potential energy surfaces
Seams between potential energy surfaces can be located and optimized by using analytic gradients within CCSD and EOM-CCSD formalisms.Properties
Properties such as transition dipoles, dipole moments, spatial extent of electron densities and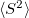
values can be computed for ADC, EOM-CCSD, EOM-OD, RAS-SF and CIS wavefunctions. Transition properties and state interactions
Matrix elements and cross sections for one- and two-photon absorption are available for EOM-EE-CCSD and ADC methods.Excited-state vibrational analysis
Given an optimized excited state geometry, Q-Chem can calculate the force constants at the stationary point to predict excited state vibrational frequencies. Stationary points can also be characterized as minima, transition structures or
th-order saddle points. Analytic excited state vibrational analysis can only be performed using the UCIS, RCIS and TDDFT methods, for which efficient analytical second derivatives are available. EOM-CCSD frequencies are also available using analytic first derivatives and second derivatives obtained from finite difference methods. EOM-OD frequencies are only available through finite difference calculations.
EOM-CC, and most of the CI codes are part of CCMAN and CCMAN2.
METHOD
Specifies the level of theory.
TYPE:
STRING
DEFAULT:
None
No Correlation
OPTIONS:
CIS
Section 6.2.1
CIS(D)
Section 6.6.1
RI-CIS(D)
Section 6.6.2
SOS-CIS(D)
Section 6.6.3
SOS-CIS(D0)
Section 6.6.4
CISD
Section 6.7.2
CISDT
Section 6.7.2
EOM-OD
Section 6.7.2
EOM-CCSD
Section 6.7.2
EOM-CCSD(dT)
Section 6.7.19
EOM-CCSD(fT)
Section 6.7.19
EOM-CC(2,3)
Section 6.7.15
ADC(0)
Section 6.8
ADC(1)
Section 6.8
ADC(2)
Section 6.8
ADC(2)-X
Section 6.8
ADC(3)
Section 6.8
SOS-ADC(2)
Section 6.8
SOS-ADC(2)-X
Section 6.8
CVS-ADC(1)
Section 6.8
CVS-ADC(2)
Section 6.8
CVS-ADC(2)-X
Section 6.8
RAS-CI
Section 6.9
RAS-CI-2
Section 6.9
RECOMMENDATION:
Consult the literature for guidance.