• Previous: Large Molecules and Linear Scaling Methods
• Up: Self-Consistent Field Ground State Methods
• Next: Hartree-Fock and Density-Functional Perturbative Corrections

4.7 Dual-Basis Self-Consistent Field Calculations

The dual-basis approximation [196, 197, 198, 199, 200, 201] to self-consistent field (HF or DFT) energies provides an efficient means for obtaining large basis set effects at vastly less cost than a full SCF calculation in a large basis set. First, a full SCF calculation is performed in a chosen small basis (specified by BASIS2). Second, a single SCF-like step in the larger, target basis (specified, as usual, by BASIS) is used to perturbatively approximate the large basis energy. This correction amounts to a first-order approximation in the change in density matrix, after the single large-basis step:

(4.92)

where 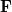(in the large basis) is built from the converged (small basis) density matrix. Thus, only a single Fock build is required in the large basis set. Currently, HF and DFT energies (SP) as well as analytic first derivatives (FORCE or OPT) are available. [Note: As of version 4.0, first derivatives of unrestricted dual-basis DFT energies—though correct—require a code-efficiency fix. We do not recommend use of these derivatives until this improvement has been made.]

Across the G3 set [202, 203, 204] of 223 molecules, using cc-pVQZ, dual-basis errors for B3LYP are 0.04 kcal/mol (energy) and 0.03 kcal/mol (atomization energy per bond) and are at least an order of magnitude less than using a smaller basis set alone. These errors are obtained at roughly an order of magnitude savings in cost, relative to the full, target-basis calculation.

4.7.1 Dual-Basis MP2

The dual-basis approximation can also be used for the reference energy of a correlated second-order Møller-Plesset (MP2) calculation [197, 201]. When activated, the dual-basis HF energy is first calculated as described above; subsequently, the MO coefficients and orbital energies are used to calculate the correlation energy in the large basis. This technique is particularly effective for RI-MP2 calculations (see Section 5.5), in which the cost of the underlying SCF calculation often dominates.

Furthermore, efficient analytic gradients of the DB-RI-MP2 energy have been developed [199] and added to Q-Chem. These gradients allow for the optimization of molecular structures with RI-MP2 near the basis set limit. Typical computational savings are on the order of 50% (aug-cc-pVDZ) to 71% (aug-cc-pVTZ). Resulting dual-basis errors are only 0.001  in molecular structures and are, again, significantly less than use of a smaller basis set alone.

4.7.2 Basis Set Pairings

We recommend using basis pairings in which the small basis set is a proper subset of the target basis (6-31G into 6-31G*, for example). They not only produce more accurate results; they also lead to more efficient integral screening in both energies and gradients. Subsets for many standard basis sets (including Dunning-style cc-pV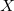Z basis sets and their augmented analogs) have been developed and thoroughly tested for these purposes. A summary of the pairings is provided in Table 4.4; details of these truncations are provided in Figure 4.1.

A new pairing for 6-31G*-type calculations is also available. The 6-4G subset (named r64G in Q-Chem) is a subset by primitive functions and provides a smaller, faster alternative for this basis set regime [200]. A case-dependent switch in the projection code (still OVPROJECTION) properly handles 6-4G. For DB-HF, the calculations proceed as described above. For DB-DFT, empirical scaling factors (see Ref. Steele:2007 for details) are applied to the dual-basis correction. This scaling is handled automatically by the code and prints accordingly.

As of Q-Chem version 3.2, the basis set projection code has also been adapted to properly account for linear dependence [201], which can often be problematic for large, augmented (aug-cc-pVTZ, etc..) basis set calculations. The same standard keyword (LINDEPTHRESH) is utilized for linear dependence in the projection code. Because of the scheme utilized to account for linear dependence, only proper-subset pairings are now allowed.

Like single-basis calculations, user-specified general or mixed basis sets may be employed (see Chapter 7) with dual-basis calculations. The target basis specification occurs in the standard $basis section. The smaller, secondary basis is placed in a similar $basis2 section; the syntax within this section is the same as the syntax for $basis. General and mixed small basis sets are activated by BASIS2=BASIS2_GEN and BASIS2=BASIS2_MIXED, respectively.

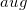Figure 4.1: Structure of the truncated basis set pairings for cc-pV(T,Q)Z and aug-cc-pV(D,T,Q)Z. The most compact functions are listed at the top. Primed functions depict (diffuse) functions. Dashes indicate eliminated functions, relative to the paired standard basis set. In each case, the truncations for hydrogen and heavy atoms are shown, along with the nomenclature used in Q-Chem.

4.7.3 Job Control

Dual-Basis calculations are controlled with the following $rem. DUAL_BASIS_ENERGY turns on the Dual-Basis approximation. Note that use of BASIS2 without DUAL_BASIS_ENERGY only uses basis set projection to generate the initial guess and does not invoke the Dual-Basis approximation (see Section 4.4.5). OVPROJECTION is used as the default projection mechanism for Dual-Basis calculations; it is not recommended that this be changed. Specification of SCF variables (e.g., THRESH) will apply to calculations in both basis sets.

DUAL_BASIS_ENERGY

Activates dual-basis SCF (HF or DFT) energy correction.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

Analytic first derivative available for HF and DFT (see JOBTYPE)

Can be used in conjunction with MP2 or RI-MP2

See BASIS, BASIS2, BASISPROJTYPE

RECOMMENDATION:

Use Dual-Basis to capture large-basis effects at smaller basis cost. Particularly useful with RI-MP2, in which HF often dominates. Use only proper subsets for small-basis calculation.

4.7.4 Examples

Example 4.67  Input for a Dual-Basis B3LYP single-point calculation.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE             sp
   METHOD              b3lyp
   BASIS               6-311++G(3df,3pd)
   BASIS2              6-311G*
   DUAL_BASIS_ENERGY   true
$end

Example 4.68  Input for a Dual-Basis B3LYP single-point calculation with a minimal 6-4G small basis.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE             sp
   METHOD              b3lyp
   BASIS               6-31G*
   BASIS2              r64G
   DUAL_BASIS_ENERGY   true
$end

Example 4.69  Input for a Dual-Basis RI-MP2 single-point calculation.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE             sp
   METHOD              rimp2
   AUX_BASIS           rimp2-cc-pVQZ
   BASIS               cc-pVQZ
   BASIS2              rcc-pVQZ   
   DUAL_BASIS_ENERGY   true
$end

Example 4.70  Input for a Dual-Basis RI-MP2 geometry optimization.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE             opt
   METHOD              rimp2
   AUX_BASIS           rimp2-aug-cc-pVDZ
   BASIS               aug-cc-pVDZ
   BASIS2              racc-pVDZ
   DUAL_BASIS_ENERGY   true
$end

Example 4.71  Input for a Dual-Basis RI-MP2 single-point calculation with mixed basis sets.

$molecule
   0 1
   H
   O   1   1.1
   H   2   1.1  1  104.5
$end

$rem
   JOBTYPE             opt
   METHOD              rimp2
   AUX_BASIS           aux_mixed
   BASIS               mixed
   BASIS2              basis2_mixed
   DUAL_BASIS_ENERGY   true
$end

$basis
 H 1
 cc-pVTZ
 ****
 O 2
 aug-cc-pVTZ
 ****
 H 3
 cc-pVTZ
 ****
$end

$basis2
 H 1
 rcc-pVTZ
 ****
 O 2
 racc-pVTZ
 ****
 H 3
 rcc-pVTZ
 ****
$end

$aux_basis
 H 1
 rimp2-cc-pVTZ
 ****
 O 2
 rimp2-aug-cc-pVTZ
 ****
 H 3
 rimp2-cc-pVTZ
 ****
$end

4.7.5 Dual-Basis Dynamics

The ability to compute SCF and MP2 energies and forces at reduced cost makes dual-basis calculations attractive for ab initio molecular dynamics simulations. Dual-basis BOMD has demonstrated [205] savings of 58%, even relative to state-of-the-art, Fock-extrapolated BOMD. Savings are further increased to 71% for dual-basis RI-MP2 dynamics. Notably, these timings outperform estimates of extended-Lagrangian (Car-Parrinello) dynamics, without detrimental energy conservation artifacts that are sometimes observed in the latter [206].

Two algorithmic factors make modest but worthwhile improvements to dual-basis dynamics. First, the iterative, small-basis calculation can benefit from Fock matrix extrapolation [206]. Second, extrapolation of the response equations (the so-called “Z-vector” equations) for nuclear forces further increases efficiency [207] . Both sets of keywords are described in Section 9.9, and the code automatically adjusts to extrapolate in the proper basis set when DUAL_BASIS_ENERGY is activated.