11.17 Population of Effectively Unpaired Electrons

In a stretched hydrogen molecule the two electrons that are paired at equilibrium forming a bond become un-paired and localized on the individual H atoms. In singlet diradicals or doublet triradicals such a weak paring exists even at equilibrium. At a single-determinant SCF level of the theory the valence electrons of a singlet system like H $_2$ remain perfectly paired, and one needs to include non-dynamical correlation to decouple the bond electron pair, giving rise to a population of effectively-unpaired (“odd”, radicalized) electrons.[Takatsuka et al.(1978)Takatsuka, Fueno, and Yamaguchi, Bochicchio(1998), Staroverov and Davidson(2000)] When the static correlation is strong, these electrons remain mostly unpaired and can be described as being localized on individual atoms.

These phenomena can be properly described within wave-function formalism. Within DFT, these effects can be described by broken-symmetry approach or by using SF-TDDFT (see Section 7.3.1). Below we describe how to derive this sort of information from pure DFT description of such low-spin open-shell systems without relying on spin-contaminated solutions.

The first-order reduced density matrix (1-RDM) corresponding to a single-determinant wave function (e.g., SCF or Kohn-Sham DFT) is idempotent:

$\begin{equation} \label{eq:gamma-idempotent} \int {\gamma }_{\sigma }^{\mathrm{SCF}}(1;2)\gamma _{\sigma }^{\mathrm{SCF}}(2;1)\: d{\mathbf{r}_{2}}={\rho }_{\sigma }({\mathbf{r}_{1}})\, , \, \, {\gamma }_{\sigma }^{\mathrm{SCF}}(1;2) = \sum _{i}^{\mathrm{occ}} \psi _{i\sigma }^{\mathrm{ks}}(1)\psi _{i\sigma }^{\mathrm{ks}}(2) \, , \end{equation}$

(11.141)

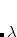where ${\rho }_{\sigma }(1)$ is the electron density of spin $\sigma$ at position ${\bf {r_{1}}}$ , and ${\mathbf{\gamma _{\sigma }^{\mathrm{SCF}}}}$ is the spin-resolved 1-RDM of a single Slater determinant. The cross product ${\gamma }_{\sigma }^{\mathrm{SCF}}(1;2)\gamma _{\sigma }^{\mathrm{SCF}}(2;1)$ reflects the Hartree-Fock exchange (or Kohn-Sham exact-exchange) governed by the HF exchange hole:

$\begin{equation} \label{eq:exactX-hole} {\gamma }_{\sigma }^{\mathrm{SCF}}(1;2)\gamma _{\sigma }^{\mathrm{SCF}}(2;1) = {\rho }_{\alpha }(1)h_{\mathrm{X}\sigma \sigma }(1,2) \, , \, \, \, \int {h}_{{\mathrm{X}}\sigma \sigma }(1,2) \: d{\bf r}_{2} = 1 \; . \end{equation}$

(11.142)

When 1-RDM includes electron correlation, it becomes non-idempotent:

$\begin{equation} \label{eq:non-idempotent1} D_{\sigma }(1)\equiv {\rho }_{\sigma }(1)-\int \gamma _{\sigma }(1;2)\gamma _{\sigma }(2;1)\: d{\mathbf{r}_{2}} \geq 0\, . \end{equation}$

(11.143)

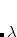The function $D_{\sigma }(1)$ measures the deviation from idempotency of the correlated 1-RDM and yields the density of effectively-unpaired (odd) electrons of spin $\sigma$ at point ${\mathbf{r}_{1}}$ .[Takatsuka et al.(1978)Takatsuka, Fueno, and Yamaguchi, Proynov(2006)] The formation of effectively-unpaired electrons in singlet systems is therefore exclusively a correlation based phenomenon. Summing $D_{\sigma }(1)$ over the spin components gives the total density of odd electrons, and integrating the latter over space gives the mean total number of odd electrons $\bar{N}_{u}$ :

$\begin{equation} \label{eq:total-odds} D_{u}(1)=2\sum _{\sigma }D_{\sigma }(1)d{\mathbf{r}_{1}},\, \, {\bar{N}}_{u}=\int D_{u}(1)d{\mathbf{r}_{1}} \, . \end{equation}$

(11.144)

The appearance of a factor of 2 in Eq. eq:total-odds above is required for reasons discussed in Ref. Proynov:2006. In Kohn-Sham DFT, the SCF 1-RDM is always idempotent which impedes the analysis of odd electron formation at that level of the theory. Ref. Proynov:2013 has proposed a remedy to this situation. It was noted that the correlated 1-RDM cross product entering Eq. eq:non-idempotent1 reflects an effective exchange, also known as cumulant exchange.[Bochicchio(1998)] The KS exact-exchange hole is itself artificially too delocalized. However, the total exchange-correlation interaction in a finite system with strong left-right (i.e., static) correlation is normally fairly localized, largely confined within a region of roughly atomic size.[Becke(2003)] The effective exchange described with the correlated 1-RDM cross product should be fairly localized as well. With this in mind, the following form of the correlated 1-RDM cross product was proposed:[Proynov et al.(2013)Proynov, Liu, and Kong]

$\begin{equation} \label{eq:b05-3} {\gamma }_{\sigma }(1;2)\, {\gamma }_{\sigma }(2;1)={\rho }_{\sigma }(1) {\bar{h}}_{{\mathrm{X}}\sigma \sigma }^{\mathrm{eff}}(1,2) \, . \end{equation}$

(11.145)

where the function ${\bar{h}}_{{\mathrm{X}}\sigma \sigma }^{\mathrm{eff}}(1;2)$ is a model DFT exchange hole of Becke-Roussel (BR) form used in Becke’s B05 method.[Becke and Johnson(2005)] The latter describes left-right static correlation effects in terms of certain effective exchange-correlation hole.[Becke and Johnson(2005)] The extra delocalization of the HF exchange hole alone is compensated by certain physically motivated real-space corrections to it:[Becke and Johnson(2005)]

$\begin{equation} \label{eq:B05-ND-XChole} {\bar{h}}_{{\mathrm{XC}}\alpha \alpha }(1,2)={\bar{h}}_{{\mathrm{X}}\alpha \alpha }^{\mathrm{eff}}(1,2) +f_{{\mathrm{c}}}(1)\, {\bar{h}}_{{\mathrm{X}}\beta \beta }^{\mathrm{eff}}(1,2)\; , \end{equation}$

(11.146)

where the BR exchange hole ${\bar{h}}_{{\mathrm{X}}\sigma \sigma }^{\mathrm{eff}}$ is used in B05 as an auxiliary function, such that the potential from the relaxed BR hole equals that of the exact-exchange hole. This results in relaxed normalization of the auxiliary BR hole less than or equal to unity:

$\begin{equation} \label{eq:BR-auxiliary} \int {\bar{h}}_{{\mathrm{X}}\sigma \sigma }^{\mathrm{eff}}(1;2)d{\mathbf{r}_{2}} =N_{X\sigma }^{\mathrm{eff}}(1)\; \leq 1\, . \end{equation}$

(11.147)

The expression of the relaxed normalization $N_{\mathrm{X}\sigma }^{\mathrm{eff}}(\mathbf{r})$ is quite complicated, but it is possible to represent it in closed analytic form.[Proynov et al.(2010)Proynov, Shao, and Kong, Proynov et al.(2012b)Proynov, Liu, Shao, and Kong] The smaller the relaxed normalization $N_{X\alpha }^{\mathrm{eff}}(1)$ , the more delocalized the corresponding exact-exchange hole.[Becke and Johnson(2005)] The $\alpha \! -\! \alpha$ exchange hole is further deepened by a fraction of the $\beta \! -\! \beta$ exchange hole, $f_{{\mathrm{c}}}(1)\, {\bar{h}}_{{\mathrm{X}}\beta \beta }^{\mathrm{eff}}(1,2)$ , which gives rise to left-right static correlation. The local correlation factor $f_{\mathrm{c}}$ in Eq.(11.146) governs this deepening and hence the strength of the static correlation at each point:[Becke and Johnson(2005)]

$\begin{equation} \label{eq:f-factor1} f_{\mathrm{c}}(\mathbf{r})=\min \left(f_{\alpha }(\mathbf{r}),\, f_{\beta }(\mathbf{r}),\, 1\right)\, ,\; \; \; 0 \leq f_{\mathrm{c}}(\mathbf{r})\, \leq 1\, \, \, , f_{\alpha }(\mathbf{r})=\frac{1-N_{\mathrm{X}\alpha }^{\mathrm{eff}}(\mathbf{r})}{N_{\mathrm{X}\beta }^{\mathrm{eff}}(\mathbf{r})}\, . \end{equation}$

(11.148)

Using Eqs. (11.148), (11.144), and (11.145), the density of odd electrons becomes:

$\begin{equation} \label{eq:non-idempotent1-1} D_{\alpha }(1)={\rho }_{\alpha }(1)(1-N_{X\alpha }^{\mathrm{eff}}(1)) \equiv {\rho }_{\alpha }(1)f_{\mathrm{c}}(1)\, N_{X\beta }^{\mathrm{eff}}(1)\, . \end{equation}$

(11.149)

The final formulas for the spin-summed odd electron density and the total mean number of odd electrons read:

$\begin{equation} \label{eq:b05-9} D_{u}(1)=4\, a_{\mathrm{nd}}^{\mathrm{op}}\; f_{\mathrm{c}}(1)\left[{\rho }_{\alpha }(1)\, N_{X\beta }^{\mathrm{eff}}(1)+{\rho }_{\beta }(1)\, N_{X\alpha }^{\mathrm{eff}}(1)\right]\; , \; \; {\bar{N}}_{u}=\int \, D_{u}(\mathbf{r_{1}})\; d\mathbf{r_{1}}\, . \end{equation}$

(11.150)

Here $a_{\mathrm{c}}^{\mathrm{nd-opp}}=0.526$ is the SCF-optimized linear coefficient of the opposite-spin static correlation energy term of the B05 functional.[Becke and Johnson(2005), Proynov et al.(2012b)Proynov, Liu, Shao, and Kong]

It is informative to decompose the total mean number of odd electrons into atomic contributions. Partitioning in real space the mean total number of odd electrons ${\bar{N}}_{u}$ as a sum of atomic contributions, we obtain the atomic population of odd electrons ( $F_{A}^{\mathrm{r}}$ ) as:

$\begin{equation} \label{eq:b05-12} F_{A}^{\mathrm{r}}=\int _{\Omega _{A}}D_{u}(\mathbf{r_{1}})\, d{\mathbf{r}_{1}}\, . \end{equation}$

(11.151)

Here $\Omega _{A}$ is a subregion assigned to atom $A$ in the system. To define these atomic regions in a simple way, we use the partitioning of the grid space into atomic subgroups within Becke’s grid-integration scheme.[Becke(1988a)] Since the present method does not require symmetry breaking, singlet states are calculated in restricted Kohn-Sham (RKS) manner even at strongly stretched bonds. This way one avoids the destructive effects that the spin contamination has on $F_{A}^{\mathrm{r}}$ and on the Kohn-Sham orbitals. The calculation of $F_{A}^{\mathrm{r}}$ can be done fully self-consistently only with the RI-B05 and RI-mB05 functionals. In these cases no special keywords are needed, just the corresponding EXCHANGE rem line for these functionals. Atomic population of odd electron can be estimated also with any other functional in two steps: first obtaining a converged SCF calculation with the chosen functional, then performing one single post-SCF iteration with RI-B05 or RI-mB05 functionals reading the guess from a preceding calculation, as shown on the input example below:

Example 11.276 To calculate the odd-electron atomic population and the correlated bond order in stretched H $_2$ , with B3LYP/RI-mB05, and with fully SCF RI-mB05

$comment
   Stretched H2: example of B3LYP calculation of the atomic population of odd electrons
   with post-SCF RI-BM05 extra iteration. 
$end

$molecule
   0 1
   H   0.  0.   0.0
   H   0.  0.   1.5000
$end

$rem
   SCF_GUESS         CORE
   METHOD            B3LYP 
   BASIS             G3LARGE
   PURECART          222
   THRESH            14
   MAX_SCF_CYCLES    80
   PRINT_INPUT       TRUE
   SCF_FINAL_PRINT   1
   INCDFT            FALSE
   XC_GRID           000128000302
   SYM_IGNORE        TRUE
   SYMMETRY          FALSE
   SCF_CONVERGENCE   9
$end

@@@

$comment
   Now one RI-B05 extra-iteration after B3LYP to generate the odd-electron atomic 
   population and the correlated bond order.
$end

$molecule
   read
$end

$rem
   SCF_GUESS         READ
   EXCHANGE          BM05 
   PURECART          22222
   BASIS             G3LARGE
   AUX_BASIS         riB05-cc-pvtz
   THRESH            14
   PRINT_INPUT       TRUE
   INCDFT            FALSE
   XC_GRID           000128000302
   SYM_IGNORE        TRUE
   SYMMETRY          FALSE
   MAX_SCF_CYCLES    0
   SCF_CONVERGENCE   9
   DFT_CUTOFFS       0
$end

@@@

$comment
   Finally, a fully SCF run RI-B05 using the previous output as a guess.
   The following input lines are obligatory here:
   PURECART     22222
   AUX_BASIS    riB05-cc-pvtz
   DFT_CUTOFFS  0
$end

$molecule
   read
$end

$rem
   SCF_GUESS        READ
   EXCHANGE         BM05 
   PURECART         22222
   BASIS            G3LARGE
   AUX_BASIS        riB05-cc-pvtz
   THRESH           14
   PRINT_INPUT      TRUE
   INCDFT           FALSE
   IPRINT           3
   XC_GRID          000128000302
   SYM_IGNORE       TRUE
   SCF_FINAL_PRINT  1
   SYMMETRY         FALSE
   MAX_SCF_CYCLES   80
   SCF_CONVERGENCE  8
   DFT_CUTOFFS      0
$end

Once the atomic population of odd electrons is obtained, a calculation of the corresponding correlated bond order of Mayer’s type follows in the code, using certain exact relationships between $F_{A}^{\mathrm{r}}$ , $F_{B}^{\mathrm{r}}$ , and the correlated bond order of Mayer type $B_{AB}$ . Both new properties are printed at the end of the output, right after the multipoles section. It is useful to compare the correlated bond order with Mayer’s SCF bond order. To print the latter, use SCF_FINAL_PRINT = 1.