Q-Chem 5.1 User’s Manual

7.6 Correlated Excited State Methods: The CIS(D) Family

CIS(D) is a simple, size-consistent doubles correction to CIS which has a computational cost scaling as the fifth power of the basis set for each excited state.[Head-Gordon et al.(1994)Head-Gordon, Rico, Oumi, and Lee, Head-Gordon et al.(1995b)Head-Gordon, Maurice, and Oumi] In this sense, CIS(D) can be considered as an excited state analog of the ground state MP2 method. CIS(D) yields useful improvements in the accuracy of excitation energies relative to CIS, and yet can be applied to relatively large molecules using Q-Chem’s efficient integrals transformation package. In addition, as in the case of MP2 method, the efficiency can be significantly improved through the use of the auxiliary basis expansions (Section 6.6).[Rhee and Head-Gordon(2007)]

7.6.1 CIS(D) Theory

The CIS(D) excited state procedure is a second-order perturbative approximation to the computationally expensive CCSD, based on a single excitation configuration interaction (CIS) reference. The coupled-cluster wave function, truncated at single and double excitations, is the exponential of the single and double substitution operators acting on the Hartree-Fock determinant:

  \begin{equation} \label{eq614} \left| \Psi \right\rangle =\exp \left( {T_1 +T_2 } \right)\left| {\Psi _0 } \right\rangle \end{equation}   (7.32)

Determination of the singles and doubles amplitudes requires solving the two equations

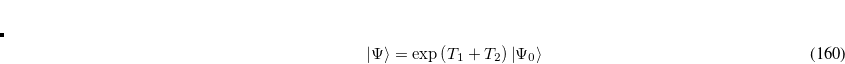  \begin{equation} \label{eq615} \left\langle {\Psi _ i^ a } \right|H-E\left| {\left( {1+T_1 +T_2 +\frac{1}{2}T_1^2 +T_1 T_2 +\frac{1}{3!}T_1^3 } \right)\Psi _0 } \right\rangle =0 \end{equation}   (7.33)

and

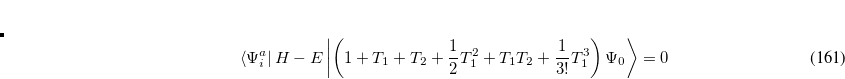  \begin{equation} \label{eq616} \left\langle {\Psi _{ij}^{ab} } \right|H-E\left| {\left( {1+T_1 +T_2 +\frac{1}{2}T_1^2 +T_1 T_2 +\frac{1}{3!}T_1^3 +\frac{1}{2}T_2^2 +\frac{1}{2}T_1^2 T_2 +\frac{1}{4!}T_1^4 } \right)\Psi _0 } \right\rangle =0 \end{equation}   (7.34)

which lead to the CCSD excited state equations. These can be written

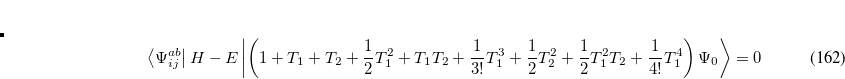  \begin{equation} \label{eq617} \left\langle {\Psi _ i^ a } \right|H-E\left| {\left( {U_1 +U_2 +T_1 U_1 +T_1 U_2 +U_1 T_2 +\frac{1}{2}T_1^2 U_1 } \right)\Psi _0 } \right\rangle =\omega b_ i^ a \end{equation}   (7.35)

and

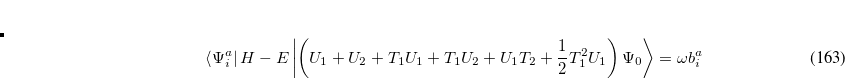  \begin{equation} \label{eq618} \begin{array}{r} \left\langle {\Psi _ i^ a } \right|H-E\left| {\left( {U_1 +U_2 +T_1 U_1 +T_1 U_2 +U_1 T_2 +\frac{1}{2}T_1^2 U_1 } \right.} \right.+T_2 U_2 \\ \left. {+\frac{1}{2}T_1^2 U_2 +T_1 T_2 U_1 +\frac{1}{3!}T_1^3 U_1 } \right|\left. {\Psi _0 } \right\rangle =\omega b_{ij}^{ab} \\ \end{array} \end{equation}   (7.36)

This is an eigenvalue equation 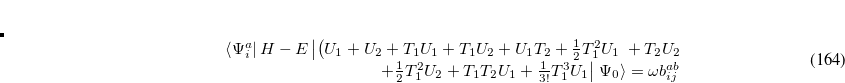$\ensuremath{\mathbf{A}}\ensuremath{\mathbf{b}} = \omega \ensuremath{\mathbf{b}}$ for the transition amplitudes (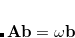$\ensuremath{\mathbf{b}}$ vectors), which are also contained in the 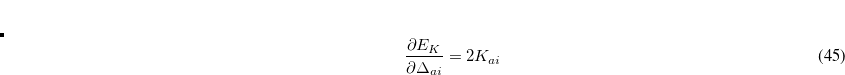$U$ operators.

The second-order approximation to the CCSD eigenvalue equation yields a second-order contribution to the excitation energy which can be written in the form

  \begin{equation} \label{eq619} \omega ^{(2)} = \ensuremath{\mathbf{b}}^{(0)^\ensuremath{\mathbf{}}{t}} {\rm {\bf A}}^{(1)} \ensuremath{\mathbf{b}}^{(1)}+ \ensuremath{\mathbf{b}}^{(0)^\ensuremath{\mathbf{}}{t}} {\rm {\bf A}}^{(2)} \ensuremath{\mathbf{b}}^{(0)} \end{equation}   (7.37)

or in the alternative form

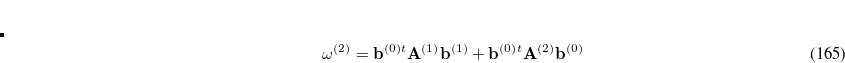  \begin{equation} \label{eq620} \omega ^{(2)}=\omega ^{\ensuremath{\mathrm{CIS(D)}}} =E^{\ensuremath{\mathrm{CIS(D)}}}-E^{\ensuremath{\mathrm{MP2}}} \end{equation}   (7.38)

where

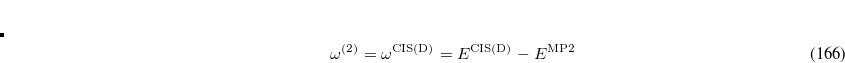  \begin{equation} \label{eq621} E^{\ensuremath{\mathrm{CIS(D)}}} = \left\langle {\Psi ^{\ensuremath{\mathrm{CIS}}}} \right|V\left| {U_2 \Psi ^{\ensuremath{\mathrm{HF}}}} \right\rangle +\left\langle {\Psi ^{\ensuremath{\mathrm{CIS}}}} \right|V\left| {T_2 U_1 \Psi ^\ensuremath{\mathrm{}}{{HF}}} \right\rangle \end{equation}   (7.39)

and

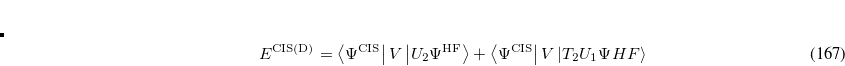  \begin{equation} \label{eq622} E^{\ensuremath{\mathrm{MP2}}} = \left\langle {\Psi ^{\ensuremath{\mathrm{HF}}}} \right|V\left| {T_2 \Psi ^{\ensuremath{\mathrm{HF}}}} \right\rangle \end{equation}   (7.40)

The output of a CIS(D) calculation contains useful information beyond the CIS(D) corrected excitation energies themselves. The stability of the CIS(D) energies is tested by evaluating a diagnostic, termed the “theta diagnostic”.[Oumi et al.(1997)Oumi, Maurice, Lee, and Head-Gordon] The theta diagnostic calculates a mixing angle that measures the extent to which electron correlation causes each pair of calculated CIS states to couple. Clearly the most extreme case would be a mixing angle of 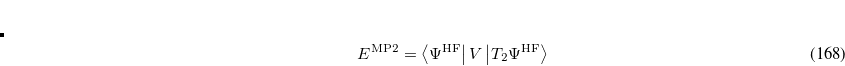$45^{\circ }$, which would indicate breakdown of the validity of the initial CIS states and any subsequent corrections. On the other hand, small mixing angles on the order of only a degree or so are an indication that the calculated results are reliable. The code can report the largest mixing angle for each state to all others that have been calculated.

7.6.2 Resolution of the Identity CIS(D) Methods

Because of algorithmic similarity with MP2 calculation, the “resolution of the identity” approximation can also be used in CIS(D). In fact, RI-CIS(D) is orders of magnitudes more efficient than previously explained CIS(D) algorithms for effectively all molecules with more than a few atoms. Like in MP2, this is achieved by reducing the prefactor of the computational load. In fact, the overall cost still scales with the fifth power of the system size.

Presently in Q-Chem, RI approximation is supported for closed-shell restricted CIS(D) and open-shell unrestricted UCIS(D) energy calculations. The theta diagnostic is not implemented for RI-CIS(D).

7.6.3 SOS-CIS(D) Model

As in MP2 case, the accuracy of CIS(D) calculations can be improved by semi-empirically scaling the opposite-spin components of CIS(D) expression:

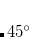  \begin{equation} E^{\ensuremath{\mathrm{SOS-CIS(D)}}} = c_ U \left\langle {\Psi ^{\ensuremath{\mathrm{CIS}}}} \right|V\left| {U_2^{\ensuremath{\mathrm{OS}}} \Psi ^{\ensuremath{\mathrm{HF}}}} \right\rangle + c_ T \left\langle {\Psi ^{\ensuremath{\mathrm{CIS}}}} \right|V\left| {T_2^{\ensuremath{\mathrm{OS}}} U_1 \Psi ^\ensuremath{\mathrm{}}{{HF}}} \right\rangle \end{equation}   (7.41)

with the corresponding ground state energy

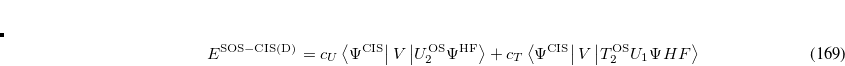  \begin{equation} E^{\ensuremath{\mathrm{SOS-MP2}}} = c_ T \left\langle {\Psi ^{\ensuremath{\mathrm{HF}}}} \right|V\left| {T_2^{\ensuremath{\mathrm{OS}}} \Psi ^{\ensuremath{\mathrm{HF}}}} \right\rangle \end{equation}   (7.42)

More importantly, this SOS-CIS(D) energy can be evaluated with the 4th power of the molecular size by adopting Laplace transform technique.[Rhee and Head-Gordon(2007)] Accordingly, SOS-CIS(D) can be applied to the calculations of excitation energies for relatively large molecules.

7.6.4 SOS-CIS(D$_0$) Model

CIS(D) and its cousins explained in the above are all based on a second-order non-degenerate perturbative correction scheme on the CIS energy (“diagonalize-and-then-perturb” scheme). Therefore, they may fail when multiple excited states come close in terms of their energies. In this case, the system can be handled by applying quasi-degenerate perturbative correction scheme (“perturb-and-then-diagonalize” scheme). The working expression can be obtained by slightly modifying CIS(D) expression shown in Section 7.6.1.[Head-Gordon et al.(1999b)Head-Gordon, Oumi, and Maurice]

First, starting from Eq. (7.37), one can be explicitly write the CIS(D) energy as[Casanova et al.(2008)Casanova, Rhee, and Head-Gordon, Head-Gordon et al.(1999b)Head-Gordon, Oumi, and Maurice]

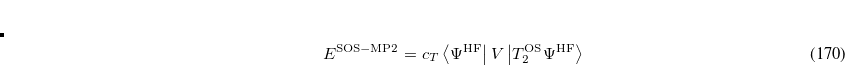  \begin{equation} \omega ^{\rm CIS} + \omega ^{(2)} = \bf b^{(0)^\ensuremath{\mathbf{}}{t}} {\rm {\bf A}_{SS}^{(0)}} \bf b^{(0)} + \bf b^{(0)^\ensuremath{\mathbf{}}{t}} {\rm {\bf A}_{SS}^{(2)}} \bf b^{(0)} - \bf b^{(0)^\ensuremath{\mathbf{}}{t}} {\rm {\bf A}_{SD}^{(1)} \left( {\bf D}_{DD}^{(0)} - \omega ^{CIS} \right)^{-1} {\bf A}_{DS}^{(1)} } \bf b^{(0)} \end{equation}   (7.43)

To avoid the failures of the perturbation theory near degeneracies, the entire single and double blocks of the response matrix should be diagonalized. Because such a diagonalization is a non-trivial non-linear problem, an additional approximation from the binomial expansion of the 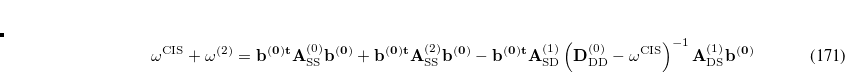$\rm \left( {\bf D}_{DD}^{(0)} - \omega ^{CIS} \right)^{-1}$ is further applied:[Head-Gordon et al.(1999b)Head-Gordon, Oumi, and Maurice]

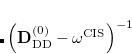  \begin{equation} \rm \left( {\bf D}_{DD}^{(0)} - \omega ^{CIS} \right)^{-1} = \left( {\bf D}_{DD}^{(0)} \right)^{-1} \left( 1 + \omega \left( {\bf D}_{DD}^{(0)} \right)^{-1} + \omega ^2 \left( {\bf D}_{DD}^{(0)} \right)^{-2} + ... \right) \end{equation}   (7.44)

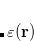The CIS(D$_0$) energy $\omega $ is defined as the eigen-solution of the response matrix with the zero-th order expansion of this equation. Namely,

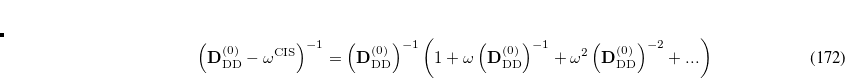  \begin{equation} \rm \left( {\bf A}_{SS}^{(0)} + {\bf A}_{SS}^{(2)} - {\bf A}_{SD}^{(1)} ( {\bf D}_{DD}^{(0)} )^{-1} {\bf A}_{DS}^{(1)} \right) \bf b = \omega \bf b \end{equation}   (7.45)

Similar to SOS-CIS(D), SOS-CIS(D$_0$) theory is defined by taking the opposite-spin portions of this equation and then scaling them with two semi-empirical parameters:[Casanova et al.(2008)Casanova, Rhee, and Head-Gordon]

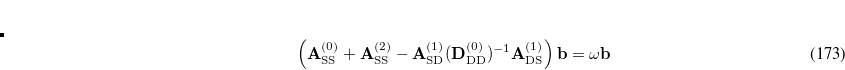  \begin{equation} \rm \left( {\bf A}_{SS}^{(0)} + {\it c_ T} {\bf A}_{SS}^{OS(2)} - {\it c_ U} {\bf A}_{SD}^{OS(1)} ( {\bf D}_{DD}^{(0)} )^{-1} {\bf A}_{DS}^{OS(1)} \right) \bf b = \omega \bf b \end{equation}   (7.46)

Using the Laplace transform and the auxiliary basis expansion techniques, this can also be handled with a 4th-order scaling computational effort. In Q-Chem, an efficient 4th-order scaling analytical gradient of SOS-CIS(D$_0$) is also available. This can be used to perform excited state geometry optimizations on the electronically excited state surfaces.

7.6.5 CIS(D) Job Control and Examples

The legacy CIS(D) algorithm in Q-Chem is handled by the CCMAN/CCMAN2 modules of Q-Chem’s and shares many of the $rem options. RI-CIS(D), SOS-CIS(D), and SOS-CIS(D$_0$) do not depend on the coupled-cluster routines. Users who will not use this legacy CIS(D) method may skip to Section 7.6.6.

As with all post-HF calculations, it is important to ensure there are sufficient resources available for the necessary integral calculations and transformations. For CIS(D), these resources are controlled using the $rem variables CC_MEMORY, MEM_STATIC and MEM_TOTAL (see Section 6.8.7).

To request a CIS(D) calculation the METHOD $rem should be set to CIS(D) and the number of excited states to calculate should be specified by EE_STATES (or EE_SINGLETS and EE_TRIPLETS when appropriate). Alternatively, CIS(D) will be performed when EXCHANGE = HF, CORRELATION = CI and EOM_CORR = CIS(D). The SF-CIS(D) is invoked by using SF_STATES.

EE_STATES

Sets the number of excited state roots to find. For closed-shell reference, defaults into EE_SINGLETS. For open-shell references, specifies all low-lying states.


TYPE:

INTEGER/INTEGER ARRAY


DEFAULT:

0

Do not look for any excited states.


OPTIONS:

$[i,j,k\ldots ]$

Find $i$ excited states in the first irrep, $j$ states in the second irrep etc.


RECOMMENDATION:

None


EE_SINGLETS

Sets the number of singlet excited state roots to find. Valid only for closed-shell references.


TYPE:

INTEGER/INTEGER ARRAY


DEFAULT:

0

Do not look for any excited states.


OPTIONS:

$[i,j,k\ldots ]$

Find $i$ excited states in the first irrep, $j$ states in the second irrep etc.


RECOMMENDATION:

None


EE_TRIPLETS

Sets the number of triplet excited state roots to find. Valid only for closed-shell references.


TYPE:

INTEGER/INTEGER ARRAY


DEFAULT:

0

Do not look for any excited states.


OPTIONS:

$[i,j,k\ldots ]$

Find $i$ excited states in the first irrep, $j$ states in the second irrep etc.


RECOMMENDATION:

None


SF_STATES

Sets the number of spin-flip target states roots to find.


TYPE:

INTEGER/INTEGER ARRAY


DEFAULT:

0

Do not look for any spin-flip states.


OPTIONS:

$[i,j,k\ldots ]$

Find $i$ SF states in the first irrep, $j$ states in the second irrep etc.


RECOMMENDATION:

None


Note: It is a symmetry of a transition rather than that of a target state which is specified in excited state calculations. The symmetry of the target state is a product of the symmetry of the reference state and the transition. For closed-shell molecules, the former is fully symmetric and the symmetry of the target state is the same as that of transition, however, for open-shell references this is not so.

CC_STATE_TO_OPT

Specifies which state to optimize.


TYPE:

INTEGER ARRAY


DEFAULT:

None


OPTIONS:

[$i$,$j$]

optimize the $j$th state of the $i$th irrep.


RECOMMENDATION:

None


Note: Since there are no analytic gradients for CIS(D), the symmetry should be turned off for geometry optimization and frequency calculations, and CC_STATE_TO_OPT should be specified assuming C$_1$ symmetry, i.e., as [1,N] where N is the number of state to optimize (the states are numbered from 1).

Example 7.120  CIS(D) excitation energy calculation for ozone at the experimental ground state geometry C$_{2v}$

$molecule
   0 1
   O 
   O  1  RE
   O  2  RE  1  A

   RE = 1.272
   A  = 116.8 
$end

$rem
   JOBTYPE            SP
   METHOD             CIS(D)
   BASIS              6-31G*
   N_FROZEN_CORE      3           use frozen core
   EE_SINGLETS        [2,2,2,2]    find 2 lowest singlets in each irrep.
   EE_TRIPLETS        [2,2,2,2]    find two lowest triplets in each irrep.
$end

Example 7.121  CIS(D) geometry optimization for the lowest triplet state of water. The symmetry is automatically turned off for finite difference calculations

$molecule
   0 1
   o
   h  1  r 
   h  1  r  2  a 

   r  0.95
   a  104.0
$end

$rem
   JOBTYPE            opt
   BASIS              3-21g
   METHOD             cis(d)
   EE_TRIPLETS        1  calculate one lowest triplet
   CC_STATE_TO_OPT    [1,1] optimize the lowest state (1st state in 1st irrep)
$end

Example 7.122  CIS(D) excitation energy and transition property calculation (between all states) for ozone at the experimental ground state geometry C$_{2v}$

$molecule
   0 1
   O
   O  1  RE
   O  2  RE  1  A

   RE = 1.272
   A  = 116.8
$end

$rem
   JOBTYPE            SP
   BASIS              6-31G*
   PURCAR             2            Non-spherical (6D)
   METHOD             CIS(D)
   EE_SINGLETS        [2,2,2,2]
   EE_TRIPLETS        [2,2,2,2]
   CC_TRANS_PROP      1
$end

7.6.6 RI-CIS(D), SOS-CIS(D), and SOS-CIS(D$_0$): Job Control

These methods are activated by setting the $rem keyword METHOD to RICIS(D), SOSCIS(D), and SOSCIS(D0), respectively. Other keywords are the same as in CIS method explained in Section 7.2.1. As these methods rely on the RI approximation, AUX_BASIS needs to be set by following the same guide as in RI-MP2 (Section 6.6).

METHOD

Excited state method of choice


TYPE:

STRING


DEFAULT:

None


OPTIONS:

RICIS(D)

Activate RI-CIS(D)

SOSCIS(D)

Activate SOS-CIS(D)

SOSCIS(D0)

Activate SOS-CIS(D$_0$)

RECOMMENDATION:

None


CIS_N_ROOTS

Sets the number of excited state roots to find


TYPE:

INTEGER


DEFAULT:

0

Do not look for any excited states


OPTIONS:

$n$

$n> 0$ Looks for $n$ excited states


RECOMMENDATION:

None


CIS_SINGLETS

Solve for singlet excited states (ignored for spin unrestricted systems)


TYPE:

LOGICAL


DEFAULT:

TRUE


OPTIONS:

TRUE

Solve for singlet states

FALSE

Do not solve for singlet states.


RECOMMENDATION:

None


CIS_TRIPLETS

Solve for triplet excited states (ignored for spin unrestricted systems)


TYPE:

LOGICAL


DEFAULT:

TRUE


OPTIONS:

TRUE

Solve for triplet states

FALSE

Do not solve for triplet states.


RECOMMENDATION:

None


SET_STATE_DERIV

Sets the excited state index for analytical gradient calculation for geometry optimizations and vibrational analysis with SOS-CIS(D$_0$)


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

$n$

Select the $n$th state.


RECOMMENDATION:

Check to see that the states do no change order during an optimization. For closed-shell systems, either CIS_SINGLETS or CIS_TRIPLETS must be set to false.


MEM_STATIC

Sets the memory for individual program modules


TYPE:

INTEGER


DEFAULT:

64

corresponding to 64 Mb


OPTIONS:

$n$

User-defined number of megabytes.


RECOMMENDATION:

At least $150(N^2 + N)D$ of MEM_STATIC is required ($N$: number of basis functions, $D$: size of a double precision storage, usually 8). Because a number of matrices with $N^2$ size also need to be stored, 32–160 Mb of additional MEM_STATIC is needed.


MEM_TOTAL

Sets the total memory available to Q-Chem


TYPE:

INTEGER


DEFAULT:

2000

2 Gb


OPTIONS:

$n$

User-defined number of megabytes


RECOMMENDATION:

The minimum memory requirement of RI-CIS(D) is approximately MEM_STATIC + max$(3SVXD, 3X^2D)$ ($S$: number of excited states, $X$: number of auxiliary basis functions, $D$: size of a double precision storage, usually 8). However, because RI-CIS(D) uses a batching scheme for efficient evaluations of electron repulsion integrals, specifying more memory will significantly speed up the calculation. Put as much memory as possible if you are not sure what to use, but never put any more than what is available. The minimum memory requirement of SOS-CIS(D) and SOS-CIS(D$_0$) is approximately MEM_STATIC + $20 X^2 D$. SOS-CIS(D$_0$) gradient calculation becomes more efficient when $30 X^2 D$ more memory space is given. Like in RI-CIS(D), put as much memory as possible if you are not sure what to use. The actual memory size used in these calculations will be printed out in the output file to give a guide about the required memory.


AO2MO_DISK

Sets the scratch space size for individual program modules


TYPE:

INTEGER


DEFAULT:

2000

2 Gb


OPTIONS:

$n$

User-defined number of megabytes.


RECOMMENDATION:

The minimum disk requirement of RI-CIS(D) is approximately $3SOVXD$. Again, the batching scheme will become more efficient with more available disk space. There is no simple formula for SOS-CIS(D) and SOS-CIS(D$_0$) disk requirement. However, because the disk space is abundant in modern computers, this should not pose any problem. Just put the available disk space size in this case. The actual disk usage information will also be printed in the output file.


SOS_FACTOR

Sets the scaling parameter $c_ T$


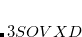
TYPE:

INTEGER


DEFAULT:

1300000

corresponding to 1.30


OPTIONS:

$n$

$c_ T = n / 1000000$


RECOMMENDATION:

Use the default


SOS_UFACTOR

Sets the scaling parameter $c_ U$


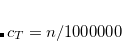
TYPE:

INTEGER


DEFAULT:

151

For SOS-CIS(D), corresponding to 1.51

140

For SOS-CIS(D$_0$), corresponding to 1.40


OPTIONS:

$n$

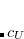
$c_ U = n / 100$


RECOMMENDATION:

Use the default


7.6.7 Examples

Example 7.123  Input for an RI-CIS(D) calculation.

$molecule
   0 1
   C     0.667472     0.000000     0.000000
   C    -0.667472     0.000000     0.000000
   H     1.237553     0.922911     0.000000
   H     1.237553    -0.922911     0.000000
   H    -1.237553     0.922911     0.000000
   H    -1.237553    -0.922911     0.000000
$end

$rem
   METHOD          ricis(d)
   BASIS           aug-cc-pVDZ
   MEM_TOTAL       1000
   MEM_STATIC      100
   AO2MO_DISK      1000
   AUX_BASIS       rimp2-aug-cc-pVDZ
   PURECART        1111
   CIS_N_ROOTS     10
   CIS_SINGLETS    true
   CIS_TRIPLETS    false
$end

Example 7.124  Input for an SOS-CIS(D) calculation.

$molecule
   0 1
   C    -0.627782     0.141553     0.000000
   O     0.730618    -0.073475     0.000000
   H    -1.133677    -0.033018    -0.942848
   H    -1.133677    -0.033018     0.942848
$end

$rem
   METHOD          soscis(d)
   BASIS           aug-cc-pVDZ
   MEM_TOTAL       1000
   MEM_STATIC      100
   AO2MO_DISK      500000     ! 0.5 Terabyte of disk space available
   AUX_BASIS       rimp2-aug-cc-pVDZ
   PURECART        1111
   CIS_N_ROOTS     5
   CIS_SINGLETS    true
   CIS_TRIPLETS    true
$end


Example 7.125  Input for an SOS-CIS(D$_0$) geometry optimization on S$_2$ surface.

$molecule
   0 1
   o
   h  1  r 
   h  1  r  2  a 

   r  0.95
   a  104.0
$end

$rem
   JOBTYPE           = opt
   METHOD            = soscis(d0)
   BASIS             = 6-31G**
   AUX_BASIS         = rimp2-VDZ
   PURECART          = 1112
   SET_STATE_DERIV   = 2
   CIS_N_ROOTS       = 5
   CIS_SINGLETS      = true
   CIS_TRIPLETS      = false
$end