Q-Chem 5.1 User’s Manual

13.7 The Second-Generation ALMO-EDA Method

The ALMO-EDA method introduced in Section 13.5 is a very useful tool for unraveling the nature of intermolecular interactions. Nevertheless, it has two major shortcomings: (i) Although the polarization (POL) energy is variationally evaluated, it does not have a meaningful basis set limit. As the employed basis set becomes larger, the POL term starts to be contaminated by charge transfer (CT) and loses its intended meaning. (ii) The frozen (FRZ) interaction is a monolithic term in the original ALMO-EDA scheme. In practice, further decomposition of the FRZ term is often desired. For example, if one wants to use ALMO-EDA as a tool for the development of empirical force fields, the separation of the FRZ term into contributions from permanent electrostatics, Pauli repulsion and dispersion will be helpful since they are usually modeled by distinct functional forms in classical force fields. These drawbacks have been addressed recently, defining the second generation of the ALMO-EDA method (also referred to as “EDA2" in the text below).[Horn and Head-Gordon(2015), Horn et al.(2016a)Horn, Mao, and Head-Gordon, Horn et al.(2016b)Horn, Mao, and Head-Gordon]

13.7.1 Generalized SCFMI Calculations and Additional Features

The original definition of the ALMOs used in SCFMI calculations is based on the fragment-blocking structure of the AO-to-MO transformation matrix, i.e., for a given fragment, the associated MOs can only be expanded by the AO basis functions centered on the atoms that belong to the same fragment. Here we propose a generalized definition for SCFMI calculations: given a set of basis vectors ($\mathbf{G}$) in which each of them is tagged to a fragment but is allowed to be spanned by any AO basis function, it defines the working basis of the SCFMI problem. Then, within this basis, the locally projected SCF equations can be solved in a similar way, with the constraint that the MO coefficient matrix in the working basis ($\mathbf{G}$) is fragment-block-diagonal, while the MO coefficient matrix in the AO basis does not necessarily retain the blocking structure. The basis vectors in $\mathbf{G}$ can be either non-orthogonal or orthogonal between fragments. More details on the generalized SCFMI equations are available in ref. Horn:2015.

This generalized SCFMI scheme is implemented in GEN_SCFMAN (the original AO-block based scheme is available in GEN_SCFMAN as well). It is used for the variational optimization of the polarized (but CT-forbidden) intermediate state in “EDA2" (see Section 13.7.2). Another preferable feature of this generalized scheme is that the interfragment linear dependency in $\mathbf{G}$ can be properly handled. Therefore, this scheme can be used to replace the original AO-block based SCFMI without becoming ill-defined when interfragment linear dependency occurs. In contrast, the original ALMO-EDA method that employs the AO-block based approach fails when the sum of the number of orbitals on each fragment is not equal to the number of orbitals for the super-system (the latter is determined by the total number of AO basis functions and BASIS_LIN_DEP_THRESH), which often happens when substantially large basis sets are used or when the super-system comprises a large number of fragments.

SCFMI calculations based on the GEN_SCFMAN implementation are triggered by setting GEN_SCFMAN = TRUE and FRGM_METHOD = STOLL or GIA (the other options of FRGM_METHOD are not allowed). A subset of supported algorithms in GEN_SCFMAN are available for restricted (R) and unrestricted (U) SCFMI, including DIIS, GDM_LS, and NEWTON_CG. While the DIIS algorithm iteratively solves for the locally-projected SCF equations, the latter two methods use the energy derivatives with respect to the on-fragment orbital rotations to minimize the energy until the gradient reaches zero. As for standard calculations using GEN_SCFMAN, internal stability analysis is also available for R- and U-SCFMI, and one can set FD_MAT_VEC_PROD to TRUE if the analytical Hessian is not available for the employed density functional.

As in the original implementation, perturbative corrections can be applied on top of the SCFMI solution to approach the full SCF result, and this is still controlled by FRGM_LPCORR. Note that among the options introduced in Section 13.6, only ARS and RS are allowed here since the exact SCF calculation is actually beyond the scope of SCFMI.

In addition, with this more general implementation users are allowed to specify some fragments to be frozen during the SCFMI calculation, i.e., intrafragment relaxation does not occur on these fragments. This is achieved by specifying the $rem variable SCFMI_FREEZE_SS. Such a calculation can be interpreted as an active fragment being embedded in a frozen environment where the interaction between them is treated quantum mechanically.

SCFMI_MODE

Determine whether generalized SCFMI is used and also the property of the working basis.


TYPE:

INTEGER


DEFAULT:

0 (“1" is used by basic “EDA2" calculations).


OPTIONS:

0

AO-block based SCFMI (the original definition of ALMOs).

1

Generalized SCFMI with basis vectors that are non-orthogonal between fragments.

2

Generalized SCFMI with basis vectors that are orthogonal between fragments.


RECOMMENDATION:

None


SCFMI_FREEZE_SS

Keep the first several fragments unrelaxed in an SCFMI calculation.


TYPE:

INTEGER


DEFAULT:

0 (all fragments are active)


OPTIONS:

$n$

Freeze the first $n$ fragments.


RECOMMENDATION:

None


Example 13.322  Generalized SCFMI calculation for the water dimer with single Roothaan-step perturbative correction. For this specific case, the result is identical to that given by AO-block based SCFMI (SCFMI_MODE = 0).

$molecule
0 1
--
0 1
O  -1.551007  -0.114520   0.000000
H  -1.934259   0.762503   0.000000
H  -0.599677   0.040712   0.000000
--
0 1
O   1.350625   0.111469   0.000000
H   1.680398  -0.373741  -0.758561
H   1.680398  -0.373741   0.758561
$end

$rem
   JOBTYPE          sp
   METHOD           b3lyp
   GEN_SCFMAN       true
   BASIS            6-31+G(d)
   GEN_SCFMAN       true
   SCF_CONVERGENCE  8
   THRESH           14
   SYMMETRY         false
   SYM_IGNORE       true
   FRGM_METHOD      stoll
   FRGM_LPCORR      rs
   SCFMI_MODE       1 !gen scfmi (non-orthogonal)
$end

13.7.2 Polarization Energy with a Well-defined Basis Set Limit

The definition of polarization energy lowering in the original ALMO-EDA used the full AO space of each fragment as the variational degrees of freedom. This is based on the assumption that the AO basis functions are fragment-ascribable based on their atomic centers. However, this assumption becomes inappropriate when very large basis sets are used, especially those with diffuse functions (e.g. def2-QZVPPD). In such scenarios, basis functions on a given fragment tend to describe other fragments so that the “absolute localization" constraint becomes weaker and finally gets effectively removed. This is why the original ALMO-EDA scheme does not have a well-defined basis set limit for its polarization energy.

To overcome this problem, Horn and Head-Gordon proposed a new definition for the POL term in the ALMO-EDA method based on fragment electrical response functions (FERFs).[Horn and Head-Gordon(2015)] FERFs on a given fragment are prepared by solving CPSCF equations after its SCF solution is found:

  \begin{equation} H_{ai, bj} (\Delta _\mu )_{bj} = (M_\mu )_{ai}, \end{equation}   (13.1)

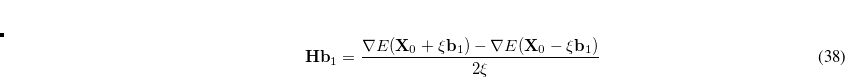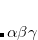where $\mathbf{H}$ is SCF orbital Hessian and $\mathbf{M}_{\mu }$ is a component ($\mu $) of a multipole matrix with a certain order. The resulting fragment response matrices ($\lbrace \Delta _{\mu }\rbrace $) are a set of $n_{\mathrm{v}} \times n_{\mathrm{o}}$ matrices. Then, a singular value decomposition (SVD) is performed on $\Delta _\mu $:

  \begin{equation} \label{eq:ferf_ cpscf} (\Delta _\mu )_{ai} = (L_\mu )_{ab}(d_\mu )_{bj}(R_{\mu }^ T)_{ji}, \end{equation}   (13.2)

and the left vectors (not including the null vectors) will be used to construct a truncated virtual space, which is used to define the variational degrees of freedom for the SCFMI problem:

  \begin{equation} \mathbf{V}_{\mu } = \mathbf{C}_{\mathrm{vir}}\mathbf{L}_{\mu }, \end{equation}   (13.3)

where $\mathbf{C}_{\mathrm{vir}}$ denotes the original virtual orbitals of the given fragment.

The basic spirit of using FERFs is to obtain a subset of virtuals that is most pertinent to the electrical polarization of a given fragment, while the redundant variational degrees of freedom (which might be CT-like) are excluded. This scheme is shown to give a well-defined basis set limit for the polarization energy that relies on the SCFMI calculation. The multipole orders (dipole (D), quadrupole (Q), and octopole (O)) included on the RHS of eq.  decide the span of FERFs on each fragment. Numerical experiments suggest that the inclusion of dipole- and quadrupole-type responses is able to long-range induced electrostatics correctly and also gives a well-defined basis set limit, which is thus recommended as the working basis of the SCFMI problem. The full span of the polarization subspace of fragment $A$ is thus:

  \begin{equation} \label{eq:pol_ ss} \mathbf{O}_ A \oplus \mathrm{span}\lbrace \mathbf{V}_{\mu x}, \mathbf{V}_{\mu y}, \mathbf{V}_{\mu z}\rbrace \oplus \mathrm{span}\lbrace \mathbf{V}_{Q2,-2}, \mathbf{V}_{Q2,-1}, \mathbf{V}_{Q2,0}, \mathbf{V}_{Q2,1}, \mathbf{V}_{Q2,2} \rbrace . \end{equation}   (13.4)

Therefore, each occupied orbital will be paired with eight virtual orbitals (if the employed AO basis is large enough).

The polarization subspaces constructed as in eq.  are non-orthogonal between fragments. Therefore, it is named as the “nDQ" model for polarization. There is another version of this method which enforces interfragment orthogonality between the polarization subspaces and it is correspondingly termed as “oDQ" (or with other multipole orders). The preparation of orthogonal FERFs is more complicated (see ref. Horn:2015 for the details) and usually gives less favorable polarization energies. For most general cases, we recommend the use of the “nDQ" model. Calculations using FERFs are performed using the generalized SCFMI procedure introduced in Section 13.7.1.

CHILD_MP

Compute FERFs for fragments and use them as the basis for SCFMI calculations.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

FALSE

Do not compute FERFs (use the full AO span of each fragment).

TRUE

Compute fragment FERFs.


RECOMMENDATION:

Use FERFs to compute polarization energy when large basis sets are used. In an “EDA2" calculation, this $rem variable is set based on the given option automatically.


CHILD_MP_ORDERS

The multipole orders included in the prepared FERFs. The last digit specifies how many multipoles to compute, and the digits in the front specify the multipole orders: 2: dipole (D); 3: quadrupole (Q); 4: octopole (O).


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

21

D

232

DQ

2343

DQO


RECOMMENDATION:

Use 232 (DQ) when FERF is needed.


Example 13.323  Generalized SCFMI calculation for the water dimer using nDQ FERFs.

$molecule
0 1
--
0 1
O  -1.551007  -0.114520   0.000000
H  -1.934259   0.762503   0.000000
H  -0.599677   0.040712   0.000000
--
0 1
O   1.350625   0.111469   0.000000
H   1.680398  -0.373741  -0.758561
H   1.680398  -0.373741   0.758561
$end

$rem
   JOBTYPE           sp
   METHOD            wb97x-v
   GEN_SCFMAN        true
   BASIS             6-31+G(d)
   GEN_SCFMAN        true
   SCF_ALGORITHM     diis
   SCF_CONVERGENCE   8
   THRESH            14
   SYMMETRY          false
   SYM_IGNORE        true
   SCF_FINAL_PRINT   1
   FRGM_METHOD       stoll
   SCFMI_MODE        1 !nonortho gen scfmi
   CHILD_MP          true
   CHILD_MP_ORDERS   232 !DQ 
   FD_MAT_VEC_PROD   false
$end

13.7.3 Further Decomposition of the Frozen Interaction Energy

The frozen interaction energy in ALMO-EDA is defined as the energy difference between the unrelaxed frozen (Heitler-London) wave function and the isolated fragments. In other literature (e.g. Ref. Hopffgarten:2012), this interaction is often decomposed in a classical fashion:

  \begin{equation} \label{eq:cls_ decomp} \Delta E_{\mathrm{frz}} = \Delta E_{\mathrm{elec}}^{\mathrm{cls}} + \Delta E_{\mathrm{pauli}}^{\mathrm{cls}}, \end{equation}   (13.5)

where the contribution from permanent electrostatics is defined as the Coulomb interaction between isolated fragment charge distributions:

  \begin{equation} \label{eq:cls_ elec} \Delta E_{\mathrm{elec}}^{\mathrm{cls}} = \sum _{A < B} \int _{r_1} \int _{r_2} \rho _{A}^{\mathrm{tot}}({\textbf r_1}) \frac{1}{{\textbf r_{12}}} \rho _{B}^{\mathrm{tot}}({\textbf r_2}) \mathrm{d}\mathbf{r}_1 \mathrm{d}\mathbf{r}_2 \end{equation}   (13.6)

and the remainder constitutes the Pauli (or exchange) term. Such a decomposition (referred to as the classical decomposition below) is associated with two issues: (i) the evaluation of permanent electrostatics makes use of the “promolecule" state (whose density is the simple sum of monomer densities) rather than a properly anti-symmetrized wave function; (ii) when dispersion-corrected density functionals are used, the Pauli term contains dispersion interaction and thus loses its original meaning.

Horn et al. proposed a new scheme to further decompose the frozen term into contributions from permanent electrostatics (ELEC), Pauli repulsion (PAULI) and dispersion (DISP):[Horn et al.(2016a)Horn, Mao, and Head-Gordon]

  \begin{equation} \label{eq:new_ decomp} \Delta E_{\mathrm{frz}} = \Delta E_{\mathrm{elec}} + \Delta E_{\mathrm{pauli}} + \Delta E_{\mathrm{disp}} \end{equation}   (13.7)

This approach is compatible with the use of all kinds of density functionals except double-hybrids, and all three components of the FRZ term are computed with the antisymmetrized frozen wave function. The key step of this method is the orthogonal decomposition of the 1PDM associated with the frozen wave function into contributions from individual fragments: $\mathbf{P}_{\mathrm{frz}} = \sum _ A \tilde{\mathbf{P}}_ A$. This is achieved by minimizing an objective function as follows:

  \begin{equation} \label{eq:kep_ obj} \Omega = \sum _{A} E_{A}[\tilde{\mathbf{P}}_ A] - E_{A}[\mathbf{P}_ A] \end{equation}   (13.8)

while interfragment orthogonality is enforced between $\tilde{\mathbf{P}}_ A$’s. The readers are referred to Ref. Horn:2016b for more details about the orthogonal decomposition.

The ELEC term is then defined as the Coulomb interaction between distorted fragment densities ($\tilde{\rho }_ A(\mathbf{r})$):

  \begin{equation} \label{eq:eda_ elec} \Delta E_{\mathrm{elec}} = \sum _{A < B} \int _{r_1} \int _{r_2} \tilde{\rho }_{A}^{\mathrm{tot}}({\textbf r_1}) \frac{1}{{\textbf r_{12}}} \tilde{\rho }_{B}^{\mathrm{tot}}({\textbf r_2}) \mathrm{d}\mathbf{r}_1 \mathrm{d}\mathbf{r}_2. \end{equation}   (13.9)

The DISP term is evaluated by subtracting the dispersion-free part of the total exchange-correlation (XC) interaction, where an auxiliary “dispersion-free" (DF) XC functional is used in company with the primary XC functional:

  \begin{equation} \label{eq:eda_ disp} \Delta E_{\mathrm{disp}} = \left(E_{\mathrm{xc}}[\mathbf{P}_{\mathrm{frz}}] - \sum _{A} E_{\mathrm{xc}}[\tilde{\mathbf{P}}_ A]\right) - \left(E_{\mathrm{xc}}^{\mathrm{DF}}[\mathbf{P}_{\mathrm{frz}}] - \sum _{A} E_{\mathrm{xc}}^{\mathrm{DF}}[\tilde{\mathbf{P}}_ A]\right). \end{equation}   (13.10)

It is suggested that HF is an appropriate DFXC to be used for dispersion-corrected hybrid functionals (e.g. $\omega $B97M-V, B3LYP-D3), while revPBE is appropriate for semi-local functionals (e.g. B97M-V).

The remainder of the frozen interaction goes into the PAULI term, which includes the net repulsive interaction given by eq.  and the “dispersion-free" part of the XC interaction:

  \begin{equation} \label{eq:eda_ pauli} \Delta E_{\mathrm{pauli}} = \sum _{A} (E_{A}[\tilde{\mathbf{P}}_ A] - E_{A}[\mathbf{P}_ A]) + \left(E_{\mathrm{xc}}^{\mathrm{DF}}[\mathbf{P}_{\mathrm{frz}}] - \sum _{A} E_{\mathrm{xc}}^{\mathrm{DF}}[\tilde{\mathbf{P}}_ A]\right). \end{equation}   (13.11)

The PAULI term and the ELEC term can also be combined together and reported as the dispersion-free frozen (DFFRZ) term if desired.

In Q-Chem’s implementation of “EDA2", the classical frozen decomposition and the new scheme defined by eqs. – are both calculated by default. The classical ELEC term only depends on monomer properties and the distances between fragments, therefore, it can be particularly useful for scenarios such as force field development (as the reference for permanent electrostatics). When the DISP term calculated by the new scheme is available, a modified classical Pauli term[Mao et al.(2016)Mao, Demerdash, Head-Gordon, and Head-Gordon] is also reported, which is simply defined as

  \begin{equation} \Delta E_{\mathrm{pauli}}^{\mathrm{mod}} = \Delta E_{\mathrm{pauli}}^{\mathrm{cls}} - \Delta E_{\mathrm{disp}}, \end{equation}   (13.12)

i.e., the dispersion contribution is removed from the classical Pauli term computed using its original definition. Alternatively, this can also be achieved without performing the orthogonal decomposition, by setting CLS_DISP to TRUE. This also evaluates the DISP term via eq.  except that undistorted monomer densities ($\mathbf{P}_ A$’s) are used instead of their distorted counterparts ($\tilde{\mathbf{P}}_ A$’s).

FRZ_ORTHO_DECOMP

Perform the decomposition of frozen interaction energy based on the orthogonal decomposition of the 1PDM associated with the frozen wave function.


TYPE:

BOOLEAN


DEFAULT:

FALSE (automatically set to TRUE by EDA2 options 1–5)


OPTIONS:

FALSE

Do not perform the orthogonal decomposition.

TRUE

Perform the frozen energy decomposition using orthogonal fragment densities.


RECOMMENDATION:

Use default value automatically set by “EDA2".


Note: Users are allowed to turn off the orthogonal decomposition by setting FRZ_ORTHO_DECOMP to -1. Also, for calculations that involve ECPs, it is automatically set to FALSE since unreasonable results will be produced otherwise.

FRZ_ORTHO_DECOMP_CONV

Convergence criterion for the minimization problem that gives the orthogonal fragment densities.


TYPE:

INTEGER


DEFAULT:

6


OPTIONS:

$n$

$10^{-n}$


RECOMMENDATION:

Use the default unless tighter convergence is preferred.


EDA_CLS_ELEC

Perform the classical decomposition of the frozen term.


TYPE:

BOOLEAN


DEFAULT:

FALSE (automatically set to TRUE by EDA2 options 1–5)


OPTIONS:

FALSE

Do not compute the classical ELEC and PAULI terms.

TRUE

Perform the classical decomposition.


RECOMMENDATION:

TRUE


EDA_CLS_DISP

Compute the DISP contribution without performing the orthogonal decomposition, which will then be subtracted from the classical PAULI term.


TYPE:

BOOLEAN


DEFAULT:

FALSE


OPTIONS:

FALSE

Use the DISP term computed with orthogonal decomposition (if available).

TRUE

Use the DISP term computed using undistorted monomer densities.


RECOMMENDATION:

Set it to TRUE when orthogonal decomposition is not performed.


DISP_FREE_X

Specify the employed “dispersion-free" exchange functional.


TYPE:

STRING


DEFAULT:

HF


OPTIONS:

Exchange functionals (e.g. revPBE) or exchange-correlation functionals (e.g. B3LYP)

supported by Q-Chem.


RECOMMENDATION:

HF is recommended for hybrid (primary) functionals (e.g.$\omega $B97X-V) and revPBE for semi-local ones (e.g.B97M-V). Other reasonable options (e.g. B3LYP for B3LYP-D3) can also be applied.


DISP_FREE_C

Specify the employed “dispersion-free" correlation functional.


TYPE:

STRING


DEFAULT:

NONE


OPTIONS:

Correlation functionals supported by Q-Chem.


RECOMMENDATION:

Put the appropriate correlation functional paired with the chosen exchange functional (e.g. put PBE if DISP_FREE_X is revPBE); put NONE if DISP_FREE_X is set to an exchange-correlation functional.


13.7.4 Job Control for EDA2

The use of the FERF model for the evaluation of polarization energy and the further decomposition of the frozen term define the second generation of the ALMO-EDA method. Meanwhile, under the same code structure, the original AO-block based ALMO model and other related methods (such as the constrained relaxation of the frozen wave function[Horn and Head-Gordon(2016)] which renders the frozen energy variationally computed, and the polMO model[Azar et al.(2013)Azar, Horn, Sundstrom, and Head-Gordon] that arguably gives a lower limit to the polarization contribution) are also available. This entire set of methods implemented in Q-Chem based on GEN_SCFMAN (see Section 4.3) is referred to as “EDA2".

The job control for EDA2 is largely simplified by a series of preset options provided by the developers. The option number is set through the EDA2 $rem variable (introduced below). Besides that, for the sake of flexibility, users are allowed to overwrite the values of part of the preset $rem variables:

EDA2

Switch on EDA2 and specify the option set number.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Do not run through EDA2.

1

Frozen energy decomposition + nDQ-FERF polarization

 

(the standard EDA2 option)

2

Frozen energy decomposition + (AO-block-based) ALMO polarization

 

(old scheme with the addition of frozen decomposition)

3

Frozen energy decomposition + oDQ-FERF polarization

 

(NOT commonly used)

4

Frozen wave function relaxation + Frozen energy decomposition + nDQ-FERF polarization

 

(NOT commonly used)

5

Frozen energy decomposition + polMO polarization

 

(NOT commonly used).

10

No preset. Completely controlled by user’s $rem input

 

(for developers only)


RECOMMENDATION:

Turn on EDA2 for Q-Chem’s ALMO-EDA jobs unless CTA with the old scheme is desired. Option 1 is recommended in general, especially when substantially large basis sets are employed. The original ALMO scheme (option 2) can be used when the employed basis set is of small or medium size (arguably no larger than augmented triple-$\zeta $). The other options are rarely used for routine applications.


Example 13.324  Energy decomposition analysis for the ammonia-borane complex. The FERF-nDQ model is used for the POL term (as very large basis set is employed here), and decomposition of the frozen interaction energy is performed (Hartree-Fock is employed as the DFXC functional by default).

$molecule
0 1
--
0 1
N         0.000000    0.000000   -0.727325
H         0.947371    0.000000   -1.091577
H        -0.473685   -0.820448   -1.091577
H        -0.473685    0.820448   -1.091577
--
0 1
B         0.000000    0.000000    0.930725
H        -1.165774    0.000000    1.243063
H         0.582887   -1.009590    1.243063
H         0.582887    1.009590    1.243063
$end

$rem
   JOBTYPE          eda 
   EDA2             1
   METHOD           wB97M-V
   BASIS            def2-QZVPPD
   SYMMETRY         false
   MEM_TOTAL        4000
   MEM_STATIC       1000
   THRESH           14  
   SCF_CONVERGENCE  8
   XC_GRID          000099000590
   NL_GRID          1   
   FD_MAT_VEC_PROD  false
$end


Example 13.325  Energy decomposition analysis of the water dimer with a low-cost model chemistry. The original ALMO model is used for the evaluation of polarization energy, and revPBE is chosen as the DFXC functional. Counterpoise correction for the BSSE is applied.

$molecule
0 1
--
0 1
H1
O1 H1 0.95641
H2 O1 0.96500  H1 104.77306
--
0 1
O2 H2 dist     O1 171.85474 H1 180.000
H3 O2 0.95822  H2 111.79807 O1 -58.587
H4 O2 0.95822  H2 111.79807 O1 58.587

dist = 2.0 
$end

$rem
   JOBTYPE          eda 
   EDA2             2
   METHOD           b97m-v
   BASIS            def2-svpd
   SCF_CONVERGENCE  8
   THRESH           14  
   SYMMETRY         false
   DISP_FREE_X      revPBE
   DISP_FREE_C      PBE 
   EDA_BSSE         true
$end