11.13 NMR and Other Magnetic Properties
The importance of nuclear magnetic resonance (NMR) spectroscopy for modern chemistry and biochemistry cannot be overestimated. Since there is no direct relationship between the measured NMR signals and structural properties, the necessity for a reliable method to predict NMR chemical shifts arises and despite tremendous progress in experimental techniques, the understanding and reliable assignment of observed experimental spectra remains often a highly difficult task. As such, quantum chemical methods can be extremely useful, both in solution and in the solid state.[Ochsenfeld(2000b), Ochsenfeld et al.(2001)Ochsenfeld, Brown, Schnell, Gauss, and Spiess, Brown et al.(2001)Brown, Schaller, Seelbach, Koziol, Ochsenfeld, Klärner, and Spiess, Ochsenfeld et al.(2002)Ochsenfeld, Koziol, Brown, Schaller, Seelbach, and Klärner, Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol]
Features of Q-Chem’s NMR package include:
Restricted Hartree-Fock and DFT calculations of NMR chemical shifts using gauge-including atomic orbitals.
Support of linear-scaling CFMM and LinK procedures (Section 4.6) to evaluate Coulomb- and exchange-like matrices.
Density matrix-based coupled-perturbed SCF approach for linear-scaling NMR calculations.
DIIS acceleration.
Support for basis sets up to
 functions.
functions. Support for LDA, GGA, and global hybrid functionals. Meta-GGA and range-separated functionals are not yet supported, nor are functionals that contain non-local correlation (e.g., those containing VV10).
Calculation of NMR chemical shifts and indirect spin-spin couplings is discussed in Section 11.13.1. Additional magnetic properties can be computed, as described in Section 11.13.3. These include hyperfine interaction tensors (electron spin–nuclear spin interaction) and nuclear quadrupole interactions with electric field gradients.
11.13.1 NMR Chemical Shifts and J-Couplings
NMR calculations are available at both the Hartree-Fock and DFT levels of theory.[Helgaker et al.(2000)Helgaker, Watson, and Handy, Sychrovský et al.(2000)Sychrovský, Gräfenstein, and Cremer] Q-Chem computes NMR chemical shielding tensors using gauge-including atomic orbitals[Ditchfield(1974), Wolinski et al.(1990)Wolinski, Hinton, and Pulay, Häser et al.(1992)Häser, Ahlrichs, Baron, Weiss, and Horn] (GIAOs), an approach that has proven to reliable and accurate for many applications.[Helgaker and Ruud(1990), Gauss(1995)] The shielding tensor  is a second-order property that depends upon the external magnetic field,
is a second-order property that depends upon the external magnetic field,  , and the spin angular momentum
, and the spin angular momentum  for a given nucleus:
for a given nucleus:
 |
(11.69) |
Using analytical derivative techniques to evaluate  , the components of this
, the components of this  tensor are computed as
tensor are computed as
 |
(11.70) |
where  indicate Cartesian components. Note that there is a separate chemical shielding tensor for each
indicate Cartesian components. Note that there is a separate chemical shielding tensor for each  , that is, for each nucleus. To compute
, that is, for each nucleus. To compute  it is necessary to solve coupled-perturbed SCF (CPSCF) equations to obtain the perturbed densities
it is necessary to solve coupled-perturbed SCF (CPSCF) equations to obtain the perturbed densities  , which can be accomplished using the MO-based “MOProp” module whose use is described below. (Use of the MOProp module to compute optical properties of molecules was discussed in Section 11.12.) Alternatively, a linear-scaling, density matrix-based CPSCF (D-CPSCF) formulation is available,[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol, Kussmann and Ochsenfeld(2007b)] which is described in Section 11.13.2.
, which can be accomplished using the MO-based “MOProp” module whose use is described below. (Use of the MOProp module to compute optical properties of molecules was discussed in Section 11.12.) Alternatively, a linear-scaling, density matrix-based CPSCF (D-CPSCF) formulation is available,[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol, Kussmann and Ochsenfeld(2007b)] which is described in Section 11.13.2.
In addition to chemical shifts, indirect nuclear spin-spin coupling constants, also known as scalar couplings or 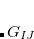 -couplings, can be computed at the SCF level. The coupling tensor
-couplings, can be computed at the SCF level. The coupling tensor  between atoms
between atoms  and
and 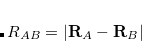 is evaluated as the second derivative of the electronic energy with respect to the nuclear magnetic moments
is evaluated as the second derivative of the electronic energy with respect to the nuclear magnetic moments  :
:
 |
(11.71) |
The indirect coupling tensor has five distinct contributions. The diamagnetic spin-orbit (DSO) contribution is calculated as an expectation value with the ground state wave function. The other contributions are the paramagnetic spin-orbit (PSO), spin-dipole (SD), Fermi contact (FC), and mixed SD/FC contributions. These terms require the electronic response of the systems to the perturbation due to the magnetic nuclei. Ten distinct CPSCF equations must be solved for each perturbing nucleus, which makes the calculation of 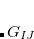 -coupling constants more time-consuming than that of chemical shifts.
-coupling constants more time-consuming than that of chemical shifts.
Some authors have recommended calculating only the Fermi contact contribution,[Bally and Rablen(2011)] and skipping the other contributions, for  -
- coupling constants. For that purpose, Q-Chem allows the user to skip calculation of any of the four contributions: (FC, SD, PSO, or DSO. (The mixed SD/FC contributions is automatically calculated at no additional cost whenever both the SD and FC contributions are computed.) See Section 11.12.2 for details. Note that omitting any of the contributions cannot be rationalized from a theoretical point of view. Results from such calculations should be interpreted extremely cautiously.
coupling constants. For that purpose, Q-Chem allows the user to skip calculation of any of the four contributions: (FC, SD, PSO, or DSO. (The mixed SD/FC contributions is automatically calculated at no additional cost whenever both the SD and FC contributions are computed.) See Section 11.12.2 for details. Note that omitting any of the contributions cannot be rationalized from a theoretical point of view. Results from such calculations should be interpreted extremely cautiously.
Note: (1) Specialized basis sets are highly recommended in any 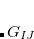 -coupling calculation. The pcJ-
-coupling calculation. The pcJ- basis set family[Jensen(2006)] has been added to the basis set library.
basis set family[Jensen(2006)] has been added to the basis set library.
(2) The Hartree-Fock level of theory is not suitable to obtain 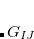 -coupling constants of any degree of reliability. Use GGA or hybrid density functionals instead.
-coupling constants of any degree of reliability. Use GGA or hybrid density functionals instead.
11.13.1.1 NMR Job Control and Examples
This section describes the use of Q-Chem’s MO-based CPSCF code, which is contained in the “MOProp” module that is also responsible for computing electric properties. NMR chemical shifts are requested by setting MOPROP = 1, and 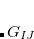 -couplings by setting JOBTYPE = ISSC. The reader is referred to to Section 11.12.2 for additional job control variables associated with the MOProp module, as well as explanations of the ones that are invoked in the samples below. An alternative,
-couplings by setting JOBTYPE = ISSC. The reader is referred to to Section 11.12.2 for additional job control variables associated with the MOProp module, as well as explanations of the ones that are invoked in the samples below. An alternative,  density matrix-based implementation of NMR chemical shifts is also available and is described in Section 11.13.2. Setting JOBTYPE = NMR invokes the density-based code, not the MO-based code.
density matrix-based implementation of NMR chemical shifts is also available and is described in Section 11.13.2. Setting JOBTYPE = NMR invokes the density-based code, not the MO-based code.
Example 11.263 MO-based NMR calculation.
$molecule
0 1
H 0.00000 0.00000 0.00000
C 1.10000 0.00000 0.00000
F 1.52324 1.22917 0.00000
F 1.52324 -0.61459 1.06450
F 1.52324 -0.61459 -1.06450
$end
$rem
METHOD B3LYP
BASIS 6-31G*
MOPROP 1
MOPROP_PERTNUM 0 ! do all perturbations at once
MOPROP_CONV_1ST 7 ! sets the CPSCF convergence threshold
MOPROP_DIIS_DIM_SS 4 ! no. of DIIS subspace vectors
MOPROP_MAXITER_1ST 100 ! max iterations
MOPROP_DIIS 5 ! turns on DIIS (=0 to turn off)
MOPROP_DIIS_THRESH 1
MOPROP_DIIS_SAVE 0
$end
In the following compound job, we show how to restart an NMR calculation should it exceed the maximum number of CPSCF iterations (specified with MOPROP_MAXITER_1ST, or should the calculation run out of time on a shared computer resource. Note that the first job is intentionally set up to exceed the maximum number of iterations, so will crash. However, the calculation is restarted and completed in the second job.
Example 11.264 Illustrates how to restart an NMR calculation.
$comment
In this first job, we *intentionally* set the max number of iterations
too small, to force premature end so that we can demonstrate restart
capability in the 2nd job.
$end
$molecule
0 1
H 0.00000 0.00000 0.00000
C 1.10000 0.00000 0.00000
F 1.52324 1.22917 0.00000
F 1.52324 -0.61459 1.06450
F 1.52324 -0.61459 -1.06450
$end
$rem
METHOD B3LYP
BASIS 6-31G*
SCF_ALGORITHM DIIS
MOPROP 1
MOPROP_MAXITER_1ST 10 ! too small, for demonstration only
GUESS_PX 1
MOPROP_DIIS_SAVE 0 ! don't hang onto the subspace vectors
$end
@@@
$molecule
0 1
H 0.00000 0.00000 0.00000
C 1.10000 0.00000 0.00000
F 1.52324 1.22917 0.00000
F 1.52324 -0.61459 1.06450
F 1.52324 -0.61459 -1.06450
$end
$rem
METHOD B3LYP
BASIS 6-31G*
SCF_GUESS READ
SKIP_SCFMAN TRUE ! no need to redo the SCF
MOPROP 1
MOPROP_RESTART 1
MOPROP_MAXITER_1ST 100 ! more reasonable choice
GUESS_PX 1
MOPROP_DIIS_SAVE 0
$end
Example 11.265 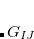 -coupling calculation: water molecule with B3LYP/cc-pVDZ
-coupling calculation: water molecule with B3LYP/cc-pVDZ
$molecule
0 1
O
H1 O OH
H2 O OH H1 HOH
OH = 0.947
HOH = 105.5
$end
$rem
JOBTYPE ISSC
EXCHANGE B3LYP
BASIS cc-pVDZ
LIN_K FALSE
SYMMETRY TRUE
MOPROP_CONV_1ST 6
$end
11.13.1.2 Nucleus-Independent Chemical Shifts: Probes of Aromaticity
Unambiguous theoretical estimates of degree of aromaticity are still on high demand. The NMR chemical shift methodology offers one unique probe of aromaticity based on one defining characteristics of an aromatic system: its ability to sustain a diatropic ring current. This leads to a response to an imposed external magnetic field with a strong (negative) shielding at the center of the ring. Schleyer et al. have employed this phenomenon to justify a new unique probe of aromaticity.[v. R. Schleyer et al.(1996)v. R. Schleyer, Maerker, Dransfield, Jiao, and van Eikema Hommes] They proposed the computed absolute magnetic shielding at ring centers (unweighted mean of the heavy-atoms ring coordinates) as a new aromaticity criterion, called nucleus-independent chemical shift (NICS). Aromatic rings show strong negative shielding at the ring center (negative NICS), while anti-aromatic systems reveal positive NICS at the ring center. As an example, a typical NICS value for benzene is about  ppm as estimated with Q-Chem at the Hartree-Fock/6-31G* level. The same NICS value for benzene was also reported in Ref. vonSchleyer:1996. The calculated NICS value for furan of
ppm as estimated with Q-Chem at the Hartree-Fock/6-31G* level. The same NICS value for benzene was also reported in Ref. vonSchleyer:1996. The calculated NICS value for furan of  ppm with Q-Chem is about the same as the value reported for furan in Ref. vonSchleyer:1996. Below is one input example of how to the NICS of furan with Q-Chem, using the ghost atom option. The ghost atom is placed at the center of the furan ring, and the basis set assigned to it within the basis mix option must be the basis used for hydrogen atom.
ppm with Q-Chem is about the same as the value reported for furan in Ref. vonSchleyer:1996. Below is one input example of how to the NICS of furan with Q-Chem, using the ghost atom option. The ghost atom is placed at the center of the furan ring, and the basis set assigned to it within the basis mix option must be the basis used for hydrogen atom.
Example 11.266 Calculation of the NMR NICS probe of furan, HF/6-31G* level. Note the ghost atom at the center of the ring.
$molecule
0 1
C -0.69480 -0.62270 -0.00550
C 0.72110 -0.63490 0.00300
C 1.11490 0.68300 0.00750
O 0.03140 1.50200 0.00230
C -1.06600 0.70180 -0.00560
H 2.07530 1.17930 0.01410
H 1.37470 -1.49560 0.00550
H -1.36310 -1.47200 -0.01090
H -2.01770 1.21450 -0.01040
GH 0.02132 0.32584 0.00034
$end
$rem
JOBTYPE NMR
METHOD HF
BASIS mixed
SCF_ALGORITHM DIIS
PURCAR 111
SEPARATE_JK 0
LIN_K 0
CFMM_ORDER 15
GRAIN 1
CFMM_PRINT 2
CFMMSTAT 1
PRINT_PATH_TIME 1
LINK_MAXSHELL_NUMBER 1
SKIP_SCFMAN 0
IGUESS core
SCF_CONVERGENCE 7
ITHRSH 10
IPRINT 23
D_SCF_CONVGUIDE 0
D_SCF_METRIC 2
D_SCF_STORAGE 50
D_SCF_RESTART 0
PRINT_PATH_TIME 1
SYM_IGNORE 1
NO_REORIENT 1
$end
$basis
C 1
6-31G*
****
C 2
6-31G*
****
C 3
6-31G*
****
O 4
6-31G*
****
C 5
6-31G*
****
H 6
6-31G*
****
H 7
6-31G*
****
H 8
6-31G*
****
H 9
6-31G*
****
H 10
6-31G*
****
11.13.2 Linear-Scaling NMR Chemical Shift Calculations
In conventional implementations, the cost for computation of NMR chemical shifts within even the simplest quantum chemical methods such as Hartree-Fock of DFT increases cubically with molecular size 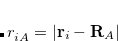 ,
,  . As such, NMR chemical shift calculations have largely been limited to molecular systems on the order of 100 atoms, assuming no symmetry. For larger systems it is crucial to reduce the increase of the computational effort to linear, which is possible for systems with a nonzero HOMO/LUMO gaps and was reported for the first time by Kussmann and Ochsenfeld.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol, Kussmann and Ochsenfeld(2007a)] This approach incurs no loss of accuracy with respect to traditional cubic-scaling implementations, and makes feasible NMR chemical shift calculations using Hartree-Fock or DFT approaches in molecular systems with 1,000+ atoms. For many molecular systems the Hartree-Fock (GIAO-HF) approach provides typically an accuracy of 0.2–0.4 ppm for the computation of
. As such, NMR chemical shift calculations have largely been limited to molecular systems on the order of 100 atoms, assuming no symmetry. For larger systems it is crucial to reduce the increase of the computational effort to linear, which is possible for systems with a nonzero HOMO/LUMO gaps and was reported for the first time by Kussmann and Ochsenfeld.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol, Kussmann and Ochsenfeld(2007a)] This approach incurs no loss of accuracy with respect to traditional cubic-scaling implementations, and makes feasible NMR chemical shift calculations using Hartree-Fock or DFT approaches in molecular systems with 1,000+ atoms. For many molecular systems the Hartree-Fock (GIAO-HF) approach provides typically an accuracy of 0.2–0.4 ppm for the computation of  H NMR chemical shifts, for example.[Ochsenfeld(2000b), Ochsenfeld et al.(2001)Ochsenfeld, Brown, Schnell, Gauss, and Spiess, Brown et al.(2001)Brown, Schaller, Seelbach, Koziol, Ochsenfeld, Klärner, and Spiess, Ochsenfeld et al.(2002)Ochsenfeld, Koziol, Brown, Schaller, Seelbach, and Klärner, Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] GIAO-HF/6-31G* calculations with 1,003 atoms and 8,593 basis functions, without symmetry, have been reported.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] GIAO-DFT calculations are even simpler and faster for density functionals that do not contain Hartree-Fock exchange.
H NMR chemical shifts, for example.[Ochsenfeld(2000b), Ochsenfeld et al.(2001)Ochsenfeld, Brown, Schnell, Gauss, and Spiess, Brown et al.(2001)Brown, Schaller, Seelbach, Koziol, Ochsenfeld, Klärner, and Spiess, Ochsenfeld et al.(2002)Ochsenfeld, Koziol, Brown, Schaller, Seelbach, and Klärner, Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] GIAO-HF/6-31G* calculations with 1,003 atoms and 8,593 basis functions, without symmetry, have been reported.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] GIAO-DFT calculations are even simpler and faster for density functionals that do not contain Hartree-Fock exchange.
The present implementation of NMR shieldings employs the LinK (linear exchange, “K”) method[Ochsenfeld et al.(1998)Ochsenfeld, White, and Head-Gordon, Ochsenfeld(2000a)] for the formation of exchange contributions.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] Since the derivative of the density matrix with respect to the magnetic field is skew-symmetric, its Coulomb-type contractions vanish. For the remaining Coulomb-type matrices the CFMM method[White et al.(1994a)White, Johnson, Gill, and Head-Gordon] is used.[Ochsenfeld et al.(2004)Ochsenfeld, Kussmann, and Koziol] In addition, a multitude of different approaches for the solution of the CPSCF equations can be selected within Q-Chem.
To request a NMR chemical shift calculation using the density matrix approach, set JOBTYPE to NMR in the $rem section. Additional job-control variables can be found below.
D_CPSCF_PERTNUM
Specifies whether to do the perturbations one at a time, or all together.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Perturbed densities to be calculated all together.
1
Perturbed densities to be calculated one at a time.
RECOMMENDATION:
None
D_SCF_CONV_1
Sets the convergence criterion for the level-1 iterations. This preconditions the density for the level-2 calculation, and does not include any two-electron integrals.
TYPE:
INTEGER
DEFAULT:
4
corresponding to a threshold of
.
OPTIONS:

Sets convergence threshold to
.
RECOMMENDATION:
The criterion for level-1 convergence must be less than or equal to the level-2 criterion, otherwise the D-CPSCF will not converge.
D_SCF_CONV_2
Sets the convergence criterion for the level-2 iterations.
TYPE:
INTEGER
DEFAULT:
4
Corresponding to a threshold of
.
OPTIONS:

Sets convergence threshold to
.
RECOMMENDATION:
None
D_SCF_MAX_1
Sets the maximum number of level-1 iterations.
TYPE:
INTEGER
DEFAULT:
100
OPTIONS:

User defined.
RECOMMENDATION:
Use the default.
D_SCF_MAX_2
Sets the maximum number of level-2 iterations.
TYPE:
INTEGER
DEFAULT:
30
OPTIONS:
User defined.
RECOMMENDATION:
Use the default.
D_SCF_DIIS
Specifies the number of matrices to use in the DIIS extrapolation in the D-CPSCF.
TYPE:
INTEGER
DEFAULT:
11
OPTIONS:

= 0 specifies no DIIS extrapolation is to be used.
RECOMMENDATION:
Use the default.
Example 11.267 NMR chemical shifts via the D-CPSCF method, showing all input options.
$molecule
0 1
H 0.00000 0.00000 0.00000
C 1.10000 0.00000 0.00000
F 1.52324 1.22917 0.00000
F 1.52324 -0.61459 1.06450
F 1.52324 -0.61459 -1.06450
$end
$rem
JOBTYPE NMR
EXCHANGE B3LYP
BASIS 6-31G*
D_CPSCF_PERTNUM 0 D-CPSCF number of perturbations at once
D_SCF_SOLVER 430 D-SCF leqs_solver
D_SCF_CONV_1 4 D-SCF leqs_conv1
D_SCF_CONV_2 4 D-SCF leqs_conv2
D_SCF_MAX_1 200 D-SCF maxiter level 1
D_SCF_MAX_2 50 D-SCF maxiter level 2
D_SCF_DIIS 11 D-SCF DIIS
D_SCF_ITOL 2 D-SCF conv. criterion
$end
11.13.3 Additional Magnetic Field-Related Properties
It is now possible to calculate certain open-shell magnetic field-related properties in Q-Chem. One is the hyperfine interaction (HFI) tensor, describing the interaction of unpaired electron spin with an atom’s nuclear spin levels:
 |
(11.72) |
where the Fermi contact (FC) contribution is
 |
(11.73) |
and the spin-dipole (SD) contribution is
 |
(11.74) |
for a nucleus  .
.
Another sensitive probe of the individual nuclear environments in a molecule is the nuclear quadrupolar interaction (NQI), arising from the interaction of a nuclei’s quadrupole moment with an applied electric field gradient (EFG), calculated as
 |
(11.75) |
for a nucleus  . Diagonalizing the tensor gives three principal values, ordered
. Diagonalizing the tensor gives three principal values, ordered  , which are components of the asymmetry parameter eta:
, which are components of the asymmetry parameter eta:
 |
(11.80) |
Both the hyperfine and EFG tensors are automatically calculated for all possible nuclei. All SCF-based methods (HF and DFT) are available with restricted and unrestricted references. Restricted open-shell references and post-HF methods are unavailable.
11.13.3.1 Job Control and Examples
Only one keyword is necessary in the $rem section to activate the magnetic property module.
MAGNET
Activate the magnetic property module.
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Don’t activate the magnetic property module.
TRUE (or 1)
Activate the magnetic property module.
RECOMMENDATION:
None.
All other options are controlled through the $magnet input section, which has the same key-value format as the $rem section (see section 3.4). Current options are:
HYPERFINE
Activate the calculation of hyperfine interaction tensors.
INPUT SECTION: $magnet
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Don’t calculate hyperfine interaction tensors.
TRUE (or 1)
Calculate hyperfine interaction tensors.
RECOMMENDATION:
None. Due to the nature of the property, which requires the spin density
, this is not meaningful for restricted (RHF) references. Only UHF (not ROHF) is available.
ELECTRIC
Activate the calculation of electric field gradient tensors.
INPUT SECTION: $magnet
TYPE:
LOGICAL
DEFAULT:
FALSE
OPTIONS:
FALSE (or 0)
Don’t calculate EFG tensors and nuclear quadrupole parameters.
TRUE (or 1)
Calculate EFG tensors and nuclear quadrupole parameters.
RECOMMENDATION:
None.
Example 11.268 Calculating hyperfine and EFG tensors for the glycine cation.
$rem
method = hf
basis = def2-sv(p)
scf_convergence = 11
thresh = 14
symmetry = false
sym_ignore = true
magnet = true
$end
$magnet
hyperfine = true
electric = true
$end
$molecule
1 2
N 0.0000000000 0.0000000000 0.0000000000
C 1.4467530000 0.0000000000 0.0000000000
C 1.9682482963 0.0000000000 1.4334965024
O 1.2385450522 0.0000000000 2.4218667010
H 1.7988742211 -0.8959881458 -0.5223754133
H 1.7997303368 0.8930070757 -0.5235632630
H -0.4722340827 -0.0025218132 0.8996536532
H -0.5080000000 0.0766867527 -0.8765335943
O 3.3107284257 -0.0000000000 1.5849828121
H 3.9426948542 -0.0000000000 0.7289954096
$end