11.14 Finite-Field Calculation of (Hyper)Polarizabilities

The dipole moment vector ( $\vec{\mu }$ ), polarizability tensor ( $\mathord {\buildrel {\lower 3pt\hbox{$\scriptscriptstyle \leftrightarrow $}} \over \alpha }$ ), first hyperpolarizability ( $\vec{\mathord {\buildrel {\lower 3pt\hbox{$\scriptscriptstyle \leftrightarrow $}} \over \beta }}$ ), and higher-order hyperpolarizabilities determine the response of the system to an applied electric field:

$\begin{equation} \label{eqn:E_ F} E(\vec{F}) = E(0)-\vec{\mu }(0)\cdot \vec{F}-\frac{1}{2!}\mathord {\buildrel {\lower 3pt\hbox{$\scriptscriptstyle \leftrightarrow $}} \over \alpha }:\vec{F}\vec{F}-\frac{1}{3!}\vec{\mathord {\buildrel {\lower 3pt\hbox{$\scriptscriptstyle \leftrightarrow $}} \over \beta }} \vdots \vec{F}\vec{F}\vec{F}-\cdots \; . \end{equation}$

(11.81)

The various polarizability tensor elements are therefore derivatives of the energy with respect to one or more electric fields, which might be frequency-dependent (dynamic polarizabilities) or not (static polarizabilities). The most efficient way to compute these properties is by analytic gradient techniques, assuming that the required derivatives have been implemented at the desired level of theory. For DFT calculations using LDA, GGAs, or global hybrid functionals the requisite analytic gradients have been implemented and their use to compute static and dynamic (hyper)polarizabilities is described in Section 11.12.

11.14.1 Numerical Calculation of Static Polarizabilities

Where analytic gradients are not available, static polarizabilities (only) can be computed via finite-difference in the applied field, which is known as the finite field (FF) approach. Beginning with Q-Chem 5.1, a sophisticated “Romberg” approach to FF differentiation is available, which includes procedures for assessing the stability of the results with respect to the finite-difference step size. The Romberg approach is described in Section 11.14.2. This section describes Q-Chem’s older approach to FF calculations based on straightforward application of small electric fields along the appropriate Cartesian directions.

Dipole moments can be calculated numerically as the first derivative of the energy with respect to $\vec{F}$ by setting JOBTYPE = DIPOLE and IDERIV = 0. If IDERIV is not specified explicitly, the dipole moment will be calculated analytically, which for post-Hartree–Fock levels of theory invokes a gradient calculation in order to utilize the relaxed wavefunction.

Similarly, set JOBTYPE = POLARIZABILITY for numerical evaluation of the static polarizability tensor $\mathord {\buildrel {\lower 3pt\hbox{$\scriptscriptstyle \leftrightarrow $}} \over \alpha }$ . This is performed by either first-order finite difference, taking first-order field derivatives of analytic dipole moments, or by second-order finite difference of the energy. The latter is useful (indeed, required) for methods where analytic gradients are not available, such as CCSD(T) for example. Note, however, that the electron cloud is formally unbound in the presence of static electric fields and therefore a bound solution is a consequence of using a finite basis set. (With analytic derivative techniques the perturbing field is infinitesimal so this is not an issue.) This fact, along with the overall sensitivity of numerical derivatives to the finite-difference step size, means that care must be taken in choosing the strength of the applied finite field.

To control the order for numerical differentiation with respect to the applied electric field, use IDERIV in the same manner as for geometric derivatives, i.e., for polarizabilties use IDERIV = 0 for second-order finite-difference of the energy and IDERIV = 1 for first-order finite difference of gradients. In addition, for numerical polarizabilities at the Hartree-Fock or DFT level set RESPONSE_POLAR = -1 in order to disable the analytic polarizability code.

RESPONSE_POLAR

Control the use of analytic or numerical polarizabilities.

TYPE:

INTEGER

DEFAULT:

0 or $-$ 1

= 0 for HF or DFT, $-$ 1 for all other methods

OPTIONS:

0

Perform an analytic polarizability calculation.

$-$ 1

Perform a numeric polarizability calculation even when analytic 2nd derivatives are available.

RECOMMENDATION:

None

In finite-difference geometric derivatives the $rem variable FDIFF_STEPSIZE controls the size of the nuclear displacements but here it controls the magnitude of the electric field perturbations:

FDIFF_STEPSIZE

Displacement used for calculating derivatives by finite difference.

TYPE:

INTEGER

DEFAULT:

1

Corresponding to $1.88973\times 10^{-5}$ a.u.

OPTIONS:

$n$

Use a step size of $n$ times the default value.

RECOMMENDATION:

Use the default unless problems arise.

11.14.2 Romberg Finite-Field Procedure

Whereas the FF procedure described in Section 11.14.1 is a straightforward, finite-difference implementation of the derivatives suggested in Eq. eqn:E_F, in the Romberg procedure[de Wergifosse et al.(2014)de Wergifosse, Liégeois, and Champagne] one combines energy values obtained for a succession of 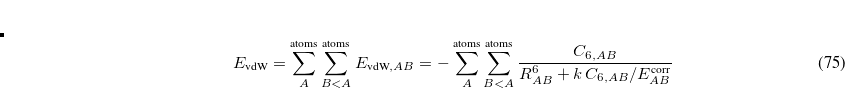$k$ external electric fields with amplitudes that form a geometric progression:

$\begin{equation} F(k)=a^ kF_0 \; . \end{equation}$

(11.82)

The FF expressions are obtained by combining truncated Taylor expansions of the energy with different amplitudes and/or external field directions. For example, in the case of the diagonal $\bm@general \boldmath \m@ne \mv@bold \bm@command \beta$ -tensor components the Romberg FF expression is

$\begin{equation} \beta _{iii}(k,0)=3 \left( \frac{ \bigl [E(F_{-i}(k+1) -E(F_{i}(k+1))\bigr ] - a\bigl [E(F_{-i}(k)-E(F_{i}(k))\bigr ] }{a(a^2-1)(a^ kF_0)^3} \right)\; . \end{equation}$

(11.83)

The field index $\pm i$ refers to the possible field directions, i.e., $\pm x$ , $\pm y$ or $\pm z$ . Truncation of the Taylor expansions means that the results are contaminated by higher-order hyperpolarizabilities, and to remove this contamination, successive “Romberg iterations” are performed using a recursive expression. For a component of a (hyper)polarizability tensor $\bm@general \boldmath \m@ne \mv@bold \bm@command {\zeta }$ , the recursive expression is

$\begin{equation} \zeta (k,n)=\frac{a^{2n}\zeta (k,n-1)-\zeta (k+1,n-1)}{a^{2n}-1} \; . \end{equation}$

(11.84)

This expression leads to a triangular Romberg table enabling monitoring of the convergence of the numerical derivative.[de Wergifosse et al.(2014)de Wergifosse, Liégeois, and Champagne]

As with any finite-difference procedure, the FF method for computing (hyper)polarizabilities is sensitive to the details of numerical differentiation. The Romberg procedure allows one to find a field window, defined by its upper and lower bounds, where the finite-difference procedure is stable. Energy values for field amplitudes below that window suffer from too-large round-off errors, which are proportional to the energy convergence threshold. The upper bound is imposed by the critical field amplitude corresponding to the intersection between the ground and excited-state energies. In the Romberg procedure, this stability window defines a sub-triangle, determination of which is the primary goal in analyzing Romberg tables.

The automatic procedure based on the analysis of field amplitude errors is implemented in scripts provided with Q-Chem’s distribution. The field amplitude error is defined as the difference between $\zeta$ -values obtained for consecutive field amplitudes at the same Romberg iteration:

$\begin{equation} \epsilon _ k(n)=\zeta (k+1,n)-\zeta (k,n) \; . \end{equation}$

(11.85)

By virtue of Romberg’s recursive expression, the field error is expected to decrease with each iteration. Convergence of the Romberg procedure can be probed using the iteration (order) error, defined as

$\begin{equation} \epsilon _ n(k)=\zeta (k,n+1)-\zeta (k,n) \; . \end{equation}$

(11.86)

Automatic analysis of these quantities is described in detail in Ref. deWergifosse:2014.

Note: (1) The automatic procedure can fail if the field window is not chosen wisely.
(2) The Romberg procedure can be performed either for one specific diagonal direction or for all Cartesian components. In the case of the second hyperpolarizability, only the $iiii$ , $iijj$ components are available.

11.14.2.1 How to execute Romberg’s differentiation procedure

To perform Romberg calculations of (hyper)polarizabilities, Q-Chem provides the following scripts in the $QC/bin/Romberg directory:

$\begin{tabbing} \hspace{1.0cm} \= \mbox{\texttt{input-Q-Chem-t-rex.sh}} \\ \> \mbox{\texttt{parse-t-rex.sh}} \\ \> \mbox{\texttt{input-Q-Chem-t-rex-3.0.f90}} \\ \> \mbox{\texttt{tddft\_ read.f90}} \\ \> \mbox{\texttt{eom\_ read.f90}} \\ \> \mbox{\texttt{T-REX-3.0.3.f90}} \end{tabbing}$

To set up a calculation, copy these files into your home directory and compile Fortran files (*.f90). The executables should be named input-Q-Chem-t-rex-3.0, tddft_read, eom_read, and T-REX. The compilation command is

$\begin{tabbing} \hspace{1.0cm} \= \mbox{\texttt{gfortran file.f90 -o file}} \end{tabbing}$

After compilation, put the binaries in the install directory (which can be the same as the directory with *.sh and inputs), and add this directory to the $PATH variable:

bash syntax: 
export PATH="$PATH":full_path_to_the_fortran_dir

csh/tsch syntax:
set path=($path full_path_to_the_fortran_dir)

(This line can be added to your .bashrc/.cshrc file for future runs.)

To run the calculation, create an input that specifies your molecule, an electronic structure method, and several additional $rem variables that (i) turn off symmetry (SYMMETRY and CC_SYMMETRY for CC/EOM calculations), (ii) request higher-precision printing (CC_PRINT_PREC), and (iii) set up very tight convergence (SCF_CONVERGENCE, CC_CONVERGENCE, EOM_DAVIDSON_CONVERGENCE, etc.). An example of an input file is given below.

Example 11.269 Input for Romberg calculations of ethylene molecule using B3LYP.

$molecule
0 1
 C        0.00000000   0.00000000 -0.66880000
 H        0.94859916   0.00000000 -1.19917145
 H       -0.94859916   0.00000000 -1.19917145
 C       -0.00000000   0.00000000  0.66880000
 H       -0.54409413   0.77704694  1.19917145
 H        0.54409413  -0.77704694  1.19917145
$end

$rem
   BASIS      =  sto-3g
   EXCHANGE   = B3lyp
   SCF_CONVERGENCE  =  13   Need tight convergence for finite field calculations
   SCF_MAX_CYCLES   =  200 
   SYMMETRY = false    All symmetries need to be turned off
   CC_PRINT_PREC = 16  16 decimal points of total energies will be printed
$end

Run the script input-Q-Chem-t-rex.sh and answer the questions regarding the parameters of the geometrical progression of field amplitudes (see example below). The script will create multiple input files for the FF calculations based on the basic input file that you provided. After running the calculations, parse the output files using the script parse-t-rex.sh. Then run the T-REX program. Answer the the questions to compute the dipole moment and (hyper)polarizabilities (see example below).

Romberg differentiation is only available for methods where printing the total energy to high precision has been enabled. In the current version of Q-Chem, CC_PRINT_PREC is implemented for the following methods: HF, DFT, MP2, RI-MP2, MP3, CCD, CCSD, CCSD(T), QCISD, QCISD(T), TDDFT, and EOM-CCSD.

Note: When using excited-state methods such as TDDFT, CIS, and EOM-CC, state ordering may switch when the external field is large.

With the T-REX program, you can compute the static dipole moment, polarizability, and first and second hyperpolarizabilities for one specific diagonal direction or for all Cartesian components, except that second hyperpolarizabilities are limited to $iiii$ and $iijj$ components. When computing all the components, you can obtain the norm of the dipole moment and polarizability, the Hyper-Rayleigh scattering first hyperpolarizability, the mean of the second hyperpolarizability, and other information

11.14.2.2 Step-by-step Example of a Finite-Field Calculation

Put the sample input file (given above) for a DFT calculation in the new directory; the name of the input file should be input. Run the input-Q-Chem-t-rex.sh script. The following questions are asked:

Components: x=1 y=2 z=3 all_beta=4 all_alpha=5
4
File name
eth-
Number of field amplitudes
5
Smallest field amplitude F_0
0.0004
a   (F_k=a^k F_0)
2.0
Number of files created         101

In this example, the answers correspond to FF calculations for $F(k)=2.0^ k \times 0.0004$ and for a geometric progression ( $k = 0,1,2,3,4,5$ ) of external field amplitudes. The calculation is set up for all the components.

After the FF calculations (i.e., after executing Q-Chem jobs for all generated inputs), parse the outputs using the parse-t-rex.sh script. The energies are written in a file called prelogfile.

Run the T-REX program and answer the questions:

Components: x=1 y=2 z=3 all_beta=4
4
Number of methods
1
Number of field amplitudes k_max+1
5
Smallest field amplitude   F_0
0.0004
Step-size a
2.0

The energies are ordered in a file called logfile and the results are printed in the results file.

0	Perform an analytic polarizability calculation.
$-$ 1	Perform a numeric polarizability calculation even when analytic 2nd derivatives are available.