Q-Chem 5.1 User’s Manual

10.3 Constrained Optimization

Constrained optimization refers to the optimization of molecular structures (transition state or minimum-energy) in which certain parameters such as bond lengths, bond angles or dihedral angles are fixed. Jon Baker’s Optimize package, implemented in Q-Chem, makes it possible to handle constraints directly in delocalized internal coordinates using the method of Lagrange multipliers (see Appendix A). Features of constrained optimization in Q-Chem are:

Constraints are imposed via the $opt input section, whose format is shown below, and the various parts of this input section are described below.

Note: As with the rest of the Q-Chem input file, the $opt section is case-insensitive, but there should be no blank space at the beginning of a line. 

$opt
CONSTRAINT
stre  atom1  atom2  value
...
bend  atom1  atom2  atom3  value
...
outp  atom1  atom2  atom3  atom4  value
...
tors  atom1  atom2  atom3  atom4  value
...
linc  atom1  atom2  atom3  atom4  value
...
linp  atom1  atom2  atom3  atom4  value
...
ENDCONSTRAINT

FIXED
atom   coordinate_reference
...
ENDFIXED

DUMMY
idum   type   list_length   defining_list
...
ENDDUMMY

CONNECT
atom   list_length   list
...
ENDCONNECT
$end

10.3.1 Geometry Optimization with General Constraints

CONSTRAINT and ENDCONSTRAINT define the beginning and end, respectively, of the constraint section of $opt within which users may specify up to six different types of constraints:

interatomic distances
Values in Ångstroms; value $> 0$:
stre   atom1   atom2   value

angles
Values in degrees, $0 \le value \le 180$; atom2 is the middle atom of the bend:
bend   atom1   atom2   atom3   value

out-of-plane-bends
Values in degrees, $-180 \le value \le 180 $ atom2; angle between atom4 and the atom1–atom2–atom3 plane:
outp   atom1   atom2   atom3   atom4   value

dihedral angles
Values in degrees, $-180 \le value \le 180$; angle the plane atom1–atom2–atom3 makes with the plane atom2–atom3–atom4:
tors   atom1   atom2   atom3   atom4   value

coplanar bends
Values in degrees, $-180 \le value \le 180$; bending of atom1–atom2–atom3 in the plane atom2–atom3–atom4:
linc   atom1   atom2   atom3   atom4   value

perpendicular bends
Values in degrees, $-180 \le value \le 180$; bending of atom1–atom2–atom3 perpendicular to the plane atom2–atom3–atom4:
linp   atom1   atom2   atom3   atom4   value

10.3.2 Frozen Atoms

Absolute atom positions can be frozen with the FIXED section. The section starts with the FIXED keyword as the first line and ends with the ENDFIXED keyword on the last. The format to fix a coordinate or coordinates of an atom is:

atom    coordinate_reference

coordinate_reference can be any combination of up to three characters 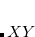$X$, $Y$ and $Z$ to specify the coordinate(s) to be fixed: 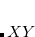$X$, $Y$, $Z$, XY, XZ, YZ, XYZ. The fixing characters must be next to each other. e.g., 

FIXED
2 XY
ENDFIXED

means the 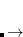$x$-coordinate and $y$-coordinate of atom 2 are fixed, whereas 

FIXED
2 X Y
ENDFIXED

will yield erroneous results.

Note: When the FIXED section is specified within $opt, the optimization will proceed in Cartesian coordinates.

10.3.3 Dummy Atoms

DUMMY defines the beginning of the dummy atom section and ENDDUMMY its conclusion. Dummy atoms are used to help define constraints during constrained optimizations in Cartesian coordinates. They cannot be used with delocalized internals.

All dummy atoms are defined with reference to a list of real atoms, that is, dummy atom coordinates are generated from the coordinates of the real atoms from the dummy atoms defining list (see below). There are three types of dummy atom:

  1. Positioned at the arithmetic mean of up to seven real atoms in the defining list.

  2. Positioned a unit distance along the normal to a plane defined by three atoms, centered on the middle atom of the three.

  3. Positioned a unit distance along the bisector of a given angle.

The format for declaring dummy atoms is: 

DUMMY
idum    type   list_length    defining_list
ENDDUMMY

idum

Center number of defining atom (must be one greater than the total number of real atoms for the first dummy atom, two greater for second etc.).

type

Type of dummy atom (either 1, 2 or 3; see above).

list_length

Number of atoms in the defining list.

defining_list

List of up to seven atoms defining the position of the dummy atom.

Once defined, dummy atoms can be used to define standard internal (distance, angle) constraints as per the constraints section, above.

Note:  The use of dummy atoms of type 1 has never progressed beyond the experimental stage.

10.3.4 Dummy Atom Placement in Dihedral Constraints

Bond and dihedral angles cannot be constrained in Cartesian optimizations to exactly $0^{\circ }$ or $\pm 180^{\circ }$. This is because the corresponding constraint normals are zero vectors. Also, dihedral constraints near these two limiting values (within, say $20^{\circ }$) tend to oscillate and are difficult to converge.

These difficulties can be overcome by defining dummy atoms and redefining the constraints with respect to the dummy atoms. For example, a dihedral constraint of $180^{\circ }$ can be redefined to two constraints of $90^{\circ }$ with respect to a suitably positioned dummy atom. The same thing can be done with a $180^{\circ }$ bond angle (long a familiar use in Z-matrix construction).

Typical usage is as shown in Table 10.2. Note that the order of atoms is important to obtain the correct signature on the dihedral angles. For a $0^{\circ }$ dihedral constraint, atoms J and K should be switched in the definition of the second torsion constraint in Cartesian coordinates.

Internal Coordinates

Cartesian Coordinates

$opt

$opt

CONSTRAINT

DUMMY

tors I J K L 180.0

M 2 I J K

ENDCONSTRAINT

ENDDUMMY

$end

CONSTRAINT

 

tors I J K M 90

 

tors M J K L 90

 

ENDCONSTRAINT

 

$end

Table 10.2: Comparison of dihedral angle constraint method for adopted coordinates.

Note: In almost all cases the above discussion is somewhat academic, as internal coordinates are now best imposed using delocalized internal coordinates and there is no restriction on the constraint values.

10.3.5 Additional Atom Connectivity

Normally delocalized internal coordinates are generated automatically from the input Cartesian coordinates. This is accomplished by first determining the atomic connectivity list (i.e., which atoms are formally bonded) and then constructing a set of individual primitive internal coordinates comprising all bond stretches, all planar bends and all proper torsions that can be generated based on the atomic connectivity. The delocalized internal are in turn constructed from this set of primitives.

The atomic connectivity depends simply on distance and there are default bond lengths between all pairs of atoms in the code. In order for delocalized internals to be generated successfully, all atoms in the molecule must be formally bonded so as to form a closed system. In molecular complexes with long, weak bonds or in certain transition states where parts of the molecule are rearranging or dissociating, distances between atoms may be too great for the atoms to be regarded as formally bonded, and the standard atomic connectivity will separate the system into two or more distinct parts. In this event, the generation of delocalized internal coordinates will fail. Additional atomic connectivity can be included for the system to overcome this difficulty.

CONNECT defines the beginning of the additional connectivity section and ENDCONNECT the end. The format of the CONNECT section is: 

CONNECT
atom   list_length   list
ENDCONNECT

atom

Atom for which additional connectivity is being defined.

list_length

Number of atoms in the list of bonded atoms.

list

List of up to 8 atoms considered as being bonded to the given atom.

Example 10.215  Methanol geometry optimization with constraints.

$comment
   Methanol geom opt with constraints in bond length and bond angles.
$end

$molecule
   0  1
   C   0.14192   0.33268   0.00000
   O   0.14192  -1.08832   0.00000
   H   1.18699   0.65619   0.00000
   H  -0.34843   0.74268   0.88786
   H  -0.34843   0.74268  -0.88786
   H  -0.77395  -1.38590   0.00000
$end

$rem
   GEOM_OPT_PRINT    6
   JOBTYPE           opt
   METHOD            hf
   BASIS             3-21g
$end

$opt
CONSTRAINT
stre  1  6  1.8
bend  2  1  4  110.0
bend  2  1  5  110.0
ENDCONSTRAINT
$end

10.3.6 Application of External Forces

In 2009, three methods for optimizing the geometry of a molecule under a constant external force were introduced, which were called Force-Modified Potential Energy Surface (FMPES),[Ong et al.(2009)Ong, Leiding, Tao, Virshup, and Mart\'{\i }nez] External Force is Explicitly Included (EFEI),[Ribas-Arino et al.(2009)Ribas-Arino, Shiga, and Marx] and Enforced Geometry Optimization (EGO).[Wolinski and Baker(2009)] These methods are closely related, and the interested reader is referred to Ref. Stauch:2016 for a detailed discussion of the similarities and differences between them. For simplicity, we will stick to the term EFEI in this Section. An EFEI calculation is a geometry optimization in which a constant that is equal to the external force is added to the nuclear gradient of two atoms specified by the user. The external force is applied along the vector connecting the two atoms, thus driving them apart. The geometry optimization converges when the restoring force of the molecule is equal to the external force. The EFEI method can also be used in AIMD simulations (see Section 10.7), in which case the force is added in every time step. The basic syntax for specifying EFEI calculations is as follows.

$efei
$atom1~ ~ ~ atom2~ ~ ~ force1$
$atom3~ ~ ~ atom4~ ~ ~ force2$
$...$
$end
Here, atom1 and atom2 are the indices of the atoms to which a force is applied. force1 is the sum of the force values that acts on atom1 and atom2 in nanoNewtons (nN). If this value is positive, a mechanical force of magnitude force1/2 acts on each of these atoms, thus driving them apart. If it is negative, an attractive force acts between the atoms. Optionally, additional pairs of atoms that are subject to a force can be specified by adding lines in the $efei section.

Example 10.216  EFEI calculation of hydrogen peroxide with a constant stretching force of 2.5 nN acting on each oxygen atom

$molecule
   0 1
   O        -0.7059250062   -0.1776745132   -0.0698000882
   O         0.7059250062    0.1776745132   -0.0698000882
   H         1.0662092915   -0.5838921799    0.4181150580
   H        -1.0662092915    0.5838921799    0.4181150580
$end

$rem
   JOBTYPE         opt
   EXCHANGE        b3lyp
   BASIS           6-31G*
$end

$efei
   1 2 5
$end