5.8 Coupled-Cluster Methods

The following sections give short summaries of the various coupled-cluster based methods available in Q-Chem, most of which are variants of coupled-cluster theory. The basic object-oriented tools necessary to permit the implementation of these methods in Q-Chem was accomplished by Profs. Anna Krylov and David Sherrill, working at Berkeley with Martin Head-Gordon, and then continuing independently at the University of Southern California and Georgia Tech, respectively. While at Berkeley, Krylov and Sherrill also developed the optimized orbital coupled-cluster method, with additional assistance from Ed Byrd. The extension of this code to MP3, MP4, CCSD and QCISD is the work of Prof. Steve Gwaltney at Berkeley, while the extensions to QCCD were implemented by Ed Byrd at Berkeley. The original tensor library and CC/EOM suite of methods are handled by the CCMAN module of Q-Chem. Recently, a new code (termed CCMAN2) has been developed in Krylov group by Evgeny Epifanovsky and others, and a gradual transition from CCMAN to CCMAN2 has began. During the transition time, both codes will be available for users via the CCMAN2 keyword.

CORRELATION

Specifies the correlation level of theory handled by CCMAN/CCMAN2.

TYPE:

STRING

DEFAULT:

None

No Correlation

OPTIONS:

CCMP2

Regular MP2 handled by CCMAN/CCMAN2

MP3

CCMAN and CCMAN2

MP4SDQ

CCMAN

MP4

CCMAN

CCD

CCMAN and CCMAN2

CCD(2)

CCMAN

CCSD

CCMAN and CCMAN2

CCSD(T)

CCMAN and CCMAN2

CCSD(2)

CCMAN

CCSD(fT)

CCMAN and CCMAN2

CCSD(dT)

CCMAN

QCISD

CCMAN and CCMAN2

QCISD(T)

CCMAN and CCMAN2

OD

CCMAN

OD(T)

CCMAN

OD(2)

CCMAN

VOD

CCMAN

VOD(2)

CCMAN

QCCD

CCMAN

QCCD(T)

CCMAN

QCCD(2)

CCMAN

VQCCD

CCMAN

VQCCD(T)

CCMAN

VQCCD(2)

CCMAN

RECOMMENDATION:

Consult the literature for guidance.

Note: All methods implemented in CCMAN2 can be executed in combination with the C-PCM implicit solvent model (section 6.7.10) and with the EFP method (section 11.5). Only energies and unrelaxed properties are available (no gradient).

5.8.1 Coupled Cluster Singles and Doubles (CCSD)

The standard approach for treating pair correlations self-consistently are coupled-cluster methods where the cluster operator contains all single and double substitutions [340], abbreviated as CCSD. CCSD yields results that are only slightly superior to MP2 for structures and frequencies of stable closed-shell molecules. However, it is far superior for reactive species, such as transition structures and radicals, for which the performance of MP2 is quite erratic.

A full textbook presentation of CCSD is beyond the scope of this manual, and several comprehensive references are available. However, it may be useful to briefly summarize the main equations. The CCSD wave function is:

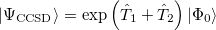$\begin{equation} \label{eq518} \left| {\Psi _{\ensuremath{\mathrm{CCSD}}} } \right\rangle =\exp \left( {\hat{T}_1 +\hat{T}_2 } \right)\left| {\Phi _0 } \right\rangle \end{equation}$

(5.24)

where the single and double excitation operators may be defined by their actions on the reference single determinant (which is normally taken as the Hartree-Fock determinant in CCSD):

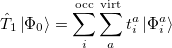$\begin{equation} \label{eq519} \hat{T}_1 \left| {\Phi _0 } \right\rangle =\sum _ i^{\ensuremath{\mathrm{occ}} } {\sum _ a^{\ensuremath{\mathrm{virt}}} {t_ i^ a } } \left| {\Phi _ i^ a } \right\rangle \end{equation}$

(5.25)

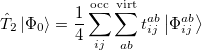$\begin{equation} \label{eq520} \hat{T}_2 \left| {\Phi _0 } \right\rangle =\frac{1}{4}\sum _{ij}^{\ensuremath{\mathrm{occ}}} {\sum _{ab}^{\ensuremath{\mathrm{virt}}} {t_{ij}^{ab} } } \left| {\Phi _{ij}^{ab} } \right\rangle \end{equation}$

(5.26)

It is not feasible to determine the CCSD energy by variational minimization of 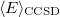$\langle E \rangle _{\ensuremath{\mathrm{CCSD}}}$ with respect to the singles and doubles amplitudes because the expressions terminate at the same level of complexity as full configuration interaction (!). So, instead, the Schrödinger equation is satisfied in the subspace spanned by the reference determinant, all single substitutions, and all double substitutions. Projection with these functions and integration over all space provides sufficient equations to determine the energy, the singles and doubles amplitudes as the solutions of sets of nonlinear equations. These equations may be symbolically written as follows:

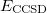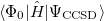$\displaystyle \label{eq521} E_{\ensuremath{\mathrm{CCSD}}}$	$\displaystyle =$	$\displaystyle \langle \Phi _0 \| \hat{H} \|\Psi _{\ensuremath{\mathrm{CCSD}}} \rangle \nonumber$
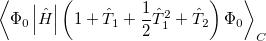$\displaystyle$	$\displaystyle =$	$\displaystyle \left\langle \Phi _0 \left\| \hat{H} \right\| \left(1+\hat{T}_1 + \frac{1}{2} \hat{T}_1^2 + \hat{T}_2 \right) \Phi _0 \right\rangle _ C$	(5.27)
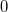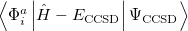$\displaystyle 0$	$\displaystyle =$	$\displaystyle \left\langle \Phi _ i^ a \left\| \hat{H}-E_{\ensuremath{\mathrm{CCSD}}} \right\|\Psi _{\ensuremath{\mathrm{CCSD}}} \right\rangle \nonumber$
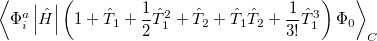$\displaystyle$	$\displaystyle =$	$\displaystyle \left\langle \Phi _ i^ a \left\| \hat{H} \right\|\left( 1+\hat{T}_1 + \frac{1}{2} \hat{T}_1^2 + \hat{T}_2 + \hat{T}_1 \hat{T}_2 + \frac{1}{3!} \hat{T}_1^3 \right)\Phi _0 \right\rangle _ C$	(5.28)
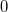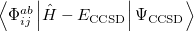$\displaystyle 0$	$\displaystyle =$	$\displaystyle \left\langle \Phi _{ij}^{ab} \left\| \hat{H}-E_{\ensuremath{\mathrm{CCSD}} } \right\|\Psi _{\ensuremath{\mathrm{CCSD}}} \right\rangle \nonumber$
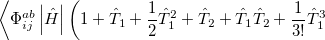$\displaystyle$	$\displaystyle =$	$\displaystyle \left\langle \Phi _{ij}^{ab} \left\| \hat{H} \right\|\left( 1+\hat{T}_1 + \frac{1}{2}\hat{T}_1^2 + \hat{T}_2 + \hat{T}_1 \hat{T}_2 + \frac{1}{3!} \hat{T}_1^3 \right.\right.\nonumber$
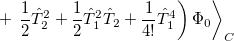$\displaystyle$	$\displaystyle$	$\displaystyle \quad \quad \quad \quad \quad \quad \quad \quad + \left.\left.\frac{1}{2}\hat{T}_2^2 + \frac{1}{2}\hat{T}_1^2 \hat{T}_2 + \frac{1}{4!}\hat{T}_1^4 \right)\Phi _0 \right\rangle _ C$	(5.29)

The result is a set of equations which yield an energy that is not necessarily variational (i.e., may not be above the true energy), although it is strictly size-consistent. The equations are also exact for a pair of electrons, and, to the extent that molecules are a collection of interacting electron pairs, this is the basis for expecting that CCSD results will be of useful accuracy.

The computational effort necessary to solve the CCSD equations can be shown to scale with the 6th power of the molecular size, for fixed choice of basis set. Disk storage scales with the 4th power of molecular size, and involves a number of sets of doubles amplitudes, as well as two-electron integrals in the molecular orbital basis. Therefore the improved accuracy relative to MP2 theory comes at a steep computational cost. Given these scalings it is relatively straightforward to estimate the feasibility (or non feasibility) of a CCSD calculation on a larger molecule (or with a larger basis set) given that a smaller trial calculation is first performed. Q-Chem supports both energies and analytic gradients for CCSD for RHF and UHF references (including frozen-core). For ROHF, only energies and unrelaxed properties are available.

5.8.2 Quadratic Configuration Interaction (QCISD)

Quadratic configuration interaction with singles and doubles (QCISD) [341] is a widely used alternative to CCSD, that shares its main desirable properties of being size-consistent, exact for pairs of electrons, as well as being also non variational. Its computational cost also scales in the same way with molecule size and basis set as CCSD, although with slightly smaller constants. While originally proposed independently of CCSD based on correcting configuration interaction equations to be size-consistent, QCISD is probably best viewed as approximation to CCSD. The defining equations are given below (under the assumption of Hartree-Fock orbitals, which should always be used in QCISD). The QCISD equations can clearly be viewed as the CCSD equations with a large number of terms omitted, which are evidently not very numerically significant:

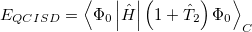$\begin{equation} \label{eq524} E_{QCISD} =\left\langle {\Phi _0 \left| {\hat{H}} \right|\left( {1+\hat{T}_2 } \right)\Phi _0 } \right\rangle _ C \end{equation}$

(5.30)

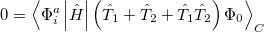$\begin{equation} \label{eq525} 0=\left\langle {\Phi _ i^ a \left| {\hat{H}} \right|\left( {\hat{T}_1 +\hat{T}_2 +\hat{T}_1 \hat{T}_2 } \right)\Phi _0 } \right\rangle _ C \end{equation}$

(5.31)

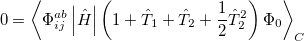$\begin{equation} \label{eq526} 0=\left\langle {\Phi _{ij}^{ab} \left| {\hat{H}} \right|\left( {1+\hat{T}_1 +\hat{T}_2 +\frac{1}{2}\hat{T}_2^2 } \right)\Phi _0 } \right\rangle _ C \end{equation}$

(5.32)

QCISD energies are available in Q-Chem, and are requested with the QCISD keyword. As discussed in Section 5.9, the non iterative QCISD(T) correction to the QCISD solution is also available to approximately incorporate the effect of higher substitutions.

5.8.3 Optimized Orbital Coupled Cluster Doubles (OD)

It is possible to greatly simplify the CCSD equations by omitting the single substitutions (i.e., setting the 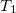$T_{1}$ operator to zero). If the same single determinant reference is used (specifically the Hartree-Fock determinant), then this defines the coupled-cluster doubles (CCD) method, by the following equations:

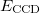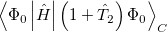	$\displaystyle \label{eq527} E_{\ensuremath{\mathrm{CCD}}}$	$\displaystyle =$	$\displaystyle \left\langle \Phi _0 \left\| \hat{H} \right\|\left( 1+\hat{T}_2 \right)\Phi _0 \right\rangle _ C$		(5.33)
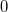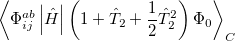	$\displaystyle 0$	$\displaystyle =$	$\displaystyle \left\langle \Phi _{ij}^{ab} \left\| \hat{H} \right\|\left( 1+\hat{T}_2 + \frac{1}{2} \hat{T}_2^2 \right)\Phi _0 \right\rangle _ C$		(5.34)

The CCD method cannot itself usually be recommended because while pair correlations are all correctly included, the neglect of single substitutions causes calculated energies and properties to be significantly less reliable than for CCSD. Single substitutions play a role very similar to orbital optimization, in that they effectively alter the reference determinant to be more appropriate for the description of electron correlation (the Hartree-Fock determinant is optimized in the absence of electron correlation).

This suggests an alternative to CCSD and QCISD that has some additional advantages. This is the optimized orbital CCD method (OO-CCD), which we normally refer to as simply optimized doubles (OD) [342]. The OD method is defined by the CCD equations above, plus the additional set of conditions that the cluster energy is minimized with respect to orbital variations. This may be mathematically expressed by

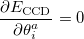$\begin{equation} \label{eq529} \frac{\partial E_{\ensuremath{\mathrm{CCD}}} }{\partial \theta _ i^ a }=0 \end{equation}$

(5.35)

where the rotation angle 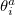$\theta _ i^ a$ mixes the $i$ th occupied orbital with the $a$ th virtual (empty) orbital. Thus the orbitals that define the single determinant reference are optimized to minimize the coupled-cluster energy, and are variationally best for this purpose. The resulting orbitals are approximate Brueckner orbitals.

The OD method has the advantage of formal simplicity (orbital variations and single substitutions are essentially redundant variables). In cases where Hartree-Fock theory performs poorly (for example artificial symmetry breaking, or non-convergence), it is also practically advantageous to use the OD method, where the HF orbitals are not required, rather than CCSD or QCISD. Q-Chem supports both energies and analytical gradients using the OD method. The computational cost for the OD energy is more than twice that of the CCSD or QCISD method, but the total cost of energy plus gradient is roughly similar, although OD remains more expensive. An additional advantage of the OD method is that it can be performed in an active space, as discussed later, in Section 5.10.

5.8.4 Quadratic Coupled Cluster Doubles (QCCD)

The non variational determination of the energy in the CCSD, QCISD, and OD methods discussed in the above subsections is not normally a practical problem. However, there are some cases where these methods perform poorly. One such example are potential curves for homolytic bond dissociation, using closed shell orbitals, where the calculated energies near dissociation go significantly below the true energies, giving potential curves with unphysical barriers to formation of the molecule from the separated fragments [343]. The Quadratic Coupled Cluster Doubles (QCCD) method [344] recently proposed by Troy Van Voorhis at Berkeley uses a different energy functional to yield improved behavior in problem cases of this type. Specifically, the QCCD energy functional is defined as

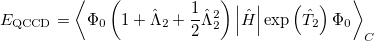$\begin{equation} \label{eq530} E_{\ensuremath{\mathrm{QCCD}}} =\left\langle {\Phi _0 \left( {1+\hat{\Lambda }_2 +\frac{1}{2}\hat{\Lambda }_2 ^2} \right)\left| {\hat{H}} \right|\exp \left( {\hat{T}_2 } \right)\Phi _0 } \right\rangle _ C \end{equation}$

(5.36)

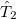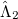where the amplitudes of both the $\hat{T}_2$ and $\hat{\Lambda }_2$ operators are determined by minimizing the QCCD energy functional. Additionally, the optimal orbitals are determined by minimizing the QCCD energy functional with respect to orbital rotations mixing occupied and virtual orbitals.

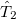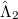To see why the QCCD energy should be an improvement on the OD energy, we first write the latter in a different way than before. Namely, we can write a CCD energy functional which when minimized with respect to the $\hat{T}_2$ and $\hat{\Lambda }_2$ operators, gives back the same CCD equations defined earlier. This energy functional is

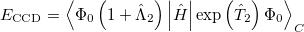$\begin{equation} \label{eq531} E_{\ensuremath{\mathrm{CCD}}} =\left\langle {\Phi _0 \left( {1+\hat{\Lambda }_2 } \right)\left| {\hat{H}} \right|\exp \left( {\hat{T}_2 } \right)\Phi _0 } \right\rangle _ C \end{equation}$

(5.37)

Minimization with respect to the 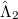$\hat{\Lambda }_2$ operator gives the equations for the 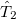$\hat{T}_2$ operator presented previously, and, if those equations are satisfied then it is clear that we do not require knowledge of the 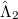$\hat{\Lambda }_2$ operator itself to evaluate the energy.

Comparing the two energy functionals, Eqs. (5.36) and (5.37), we see that the QCCD functional includes up through quadratic terms of the Maclaurin expansion of 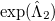$\exp (\hat{\Lambda }_2)$ while the conventional CCD functional includes only linear terms. Thus the bra wave function and the ket wave function in the energy expression are treated more equivalently in QCCD than in CCD. This makes QCCD closer to a true variational treatment [343] where the bra and ket wave functions are treated precisely equivalently, but without the exponential cost of the variational method.

In practice QCCD is a dramatic improvement relative to any of the conventional pair correlation methods for processes involving more than two active electrons (i.e., the breaking of at least a double bond, or, two spatially close single bonds). For example calculations, we refer to the original paper [344], and the follow-up paper describing the full implementation [345]. We note that these improvements carry a computational price. While QCCD scales formally with the 6th power of molecule size like CCSD, QCISD, and OD, the coefficient is substantially larger. For this reason, QCCD calculations are by default performed as OD calculations until they are partly converged. Q-Chem also contains some configuration interaction models (CISD and CISDT). The CI methods are inferior to CC due to size-consistency issues, however, these models may be useful for benchmarking and development purposes.

5.8.5 Resolution of the Identity with CC (RI-CC)

The RI approximation (see Section 5.6) can be used in coupled-cluster calculations, which substantially reduces the cost of integral transformation and disk storage requirements. The RI approximations may be used for integrals only such that integrals are generated in conventional MO form and canonical CC/EOM calculations are performed, or in a more complete version when modified CC/EOM equations are used such that the integrals are used in their RI representation. The latter version allows for more substantial savings in storage and in computational speed-up.

The RI for integrals is invoked when AUX_BASIS is specified. All two-electron integrals are used in RI decomposed form in CC when AUX_BASIS is specified.

By default, the integrals will be stored in the RI form and special CC/EOM code will be invoked. Keyword CC_DIRECT_RI allows one to use RI generated integrals in conventional form (by transforming RI integrals back to the standard format) invoking conventional CC procedures.

Note: RI for integrals is available for all CCMAN/CCMAN2 methods. CCMAN requires that the unrestricted reference be used, CCMAN2 does not have this limitation. In addition, while RI is available for jobs that need analytical gradients, only energies and properties are computed using RI. Energy derivatives are calculated using regular electron repulsion integral derivatives. Full RI implementation (with integrals used in decomposed form) is only available for CCMAN2. For maximum computational efficiency, combine with FNO (see Sections 5.11 and 6.7.7) when appropriate.

5.8.6 Cholesky decomposition with CC (CD-CC)

Two-electron integrals can be decomposed using Cholesky decomposition [346] giving rise to the same representation as in RI and substantially reducing the cost of integral transformation, disk storage requirements, and improving parallel performance:

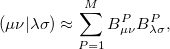$\begin{equation} (\mu \nu \vert \lambda \sigma ) \approx \sum _{P=1}^ M B_{\mu \nu }^ P B_{\lambda \sigma }^ P, \end{equation}$

(5.38)

The rank of Cholesky decomposition, 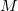$M$ , is typically 3-10 times larger than the number of basis functions 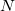$N$ (Ref. Aquilante:2009); it depends on the decomposition threshold 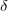$\delta$ and is considerably smaller than the full rank of the matrix, 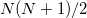$N(N+1)/2$ (Refs. Aquilante:2009,Beebe:1977,Wilson:1990). Cholesky decomposition removes linear dependencies in product densities [347] 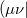$(\mu \nu \vert$ allowing one to obtain compact approximation to the original matrix with accuracy, in principle, up to machine precision.

Decomposition threshold 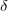$\delta$ is the only parameter that controls accuracy and the rank of the decomposition. Cholesky decomposition is invoked by specifying CHOLESKY_TOL that defines the accuracy with which decomposition should be performed. For most calculations tolerance of 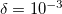$\delta = 10^{-3}$ gives a good balance between accuracy and compactness of the rank. Tolerance of 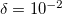$\delta = 10^{-2}$ can be used for exploratory calculations and 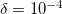$\delta = 10^{-4}$ for high-accuracy calculations. Similar to RI, Cholesky-decomposed integrals can be transformed back, into the canonical MO form, using CC_DIRECT_RI keyword.

Note: Cholesky decomposition is available for all CCMAN2 methods. Analytic gradients are not yet available; only energies and properties are computed using CD. For maximum computational efficiency, combine with FNO (see Sections 5.11 and 6.7.7) when appropriate.

5.8.7 Job Control Options

There are a large number of options for the coupled-cluster singles and doubles methods. They are documented in Appendix C, and, as the reader will find upon following this link, it is an extensive list indeed. Fortunately, many of them are not necessary for routine jobs. Most of the options for non-routine jobs concern altering the default iterative procedure, which is most often necessary for optimized orbital calculations (OD, QCCD), as well as the active space and EOM methods discussed later in Section 5.10. The more common options relating to convergence control are discussed there, in Section 5.10.5. Below we list the options that one should be aware of for routine calculations.

For memory options and parallel execution, see Section 5.14.

CC_CONVERGENCE

Overall convergence criterion for the coupled-cluster codes. This is designed to ensure at least $n$ significant digits in the calculated energy, and automatically sets the other convergence-related variables (CC_E_CONV, CC_T_CONV, CC_THETA_CONV, CC_THETA_GRAD_CONV) [ $10^{-n}$ ].

TYPE:

INTEGER

DEFAULT:

6

Energies.

7

Gradients.

OPTIONS:

$n$

Corresponding to $10^{-n}$ convergence criterion. Amplitude convergence is set

automatically to match energy convergence.

RECOMMENDATION:

Use the default

Note: For single point calculations, CC_E_CONV=6 and CC_T_CONV=4. Tighter amplitude convergence (CC_T_CONV=5) is used for gradients and EOM calculations.

CC_DOV_THRESH

Specifies minimum allowed values for the coupled-cluster energy denominators. Smaller values are replaced by this constant during early iterations only, so the final results are unaffected, but initial convergence is improved when the HOMO-LUMO gap is small or when non-conventional references are used.

TYPE:

INTEGER

DEFAULT:

0

OPTIONS:

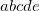
$abcde$

Integer code is mapped to $abc\times 10^{-de}$ , e.g., $2502$ corresponds to 0.25

RECOMMENDATION:

Increase to 0.25, 0.5 or 0.75 for non convergent coupled-cluster calculations.

CC_SCALE_AMP

If not 0, scales down the step for updating coupled-cluster amplitudes in cases of problematic convergence.

TYPE:

INTEGER

DEFAULT:

0

no scaling

OPTIONS:

$abcd$

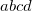
Integer code is mapped to $abcd\times 10^{-2}$ , e.g., $90$ corresponds to 0.9

RECOMMENDATION:

Use 0.9 or 0.8 for non convergent coupled-cluster calculations.

CC_MAX_ITER

Maximum number of iterations to optimize the coupled-cluster energy.

TYPE:

INTEGER

DEFAULT:

200

OPTIONS:

$n$

up to $n$ iterations to achieve convergence.

RECOMMENDATION:

None

CC_PRINT

Controls the output from post-MP2 coupled-cluster module of Q-Chem

TYPE:

INTEGER

DEFAULT:

1

OPTIONS:

$0-7$

higher values can lead to deforestation…

RECOMMENDATION:

Increase if you need more output and don’t like trees

CHOLESKY_TOL

Tolerance of Cholesky decomposition of two-electron integrals

TYPE:

INTEGER

DEFAULT:

3

OPTIONS:

$n$

Corresponds to a tolerance of $10^{-n}$

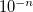
RECOMMENDATION:

2 - qualitative calculations, 3 - appropriate for most cases, 4 - quantitative (error in total energy typically less than 1 $\mu$ hartree)

CC_DIRECT_RI

Controls use of RI and Cholesky integrals in conventional (undecomposed) form

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

use all integrals in decomposed format

TRUE

transform all RI or Cholesky integral back to conventional format

RECOMMENDATION:

By default all integrals are used in decomposed format allowing significant reduction of memory use. If all integrals are transformed back (TRUE option) no memory reduction is achieved and decomposition error is introduced, however, the integral transformation is performed significantly faster and conventional CC/EOM algorithms are used.

5.8.8 Examples

Example 5.87 A series of jobs evaluating the correlation energy (with core orbitals frozen) of the ground state of the NH $_{2}$ radical with three methods of coupled-cluster singles and doubles type: CCSD itself, OD, and QCCD.

$molecule
   0  2
   N
   H1  N  1.02805
   H2  N  1.02805  H1  103.34
$end

$rem
   METHOD          ccsd
   BASIS           6-31g*
   N_FROZEN_CORE   fc
$end

@@@

$molecule
   read
$end

$rem
   METHOD          od
   BASIS           6-31g*
   N_FROZEN_CORE   fc
$end

@@@

$molecule
   read
$end

$rem
   METHOD          qccd
   BASIS           6-31g*
   N_FROZEN_CORE   fc
$end

Example 5.88 A job evaluating CCSD energy of water using RI-CCSD

$molecule
  0 1
  O
  H1 O OH
  H2 O OH H1 HOH

  OH  = 0.947
  HOH = 105.5
$end

$rem
   METHOD          ccsd
   BASIS           aug-cc-pvdz
   AUX_BASIS       rimp2-aug-cc-pvdz
$end

Example 5.89 A job evaluating CCSD energy of water using CD-CCSD (tolerance = 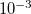$10^{-3}$ )

$molecule
  0 1
  O
  H1 O OH
  H2 O OH H1 HOH

  OH  = 0.947
  HOH = 105.5
$end

$rem
   METHOD          ccsd
   BASIS           aug-cc-pvdz
   CHOLESKY_TOL    3
$end

Example 5.90 A job evaluating CCSD energy of water using CD-CCSD (tolerance = 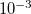$10^{-3}$ ) with FNO

$molecule
   0 1
   O
   H1 O OH
   H2 O OH H1 HOH

   OH  = 0.947
   HOH = 105.5
$end

$rem
   METHOD          ccsd
   BASIS           aug-cc-pvdz
   CHOLESKY_TOL    3
   CC_FNO_THRESH   9950
$end

CCMP2	Regular MP2 handled by CCMAN/CCMAN2
MP3	CCMAN and CCMAN2
MP4SDQ	CCMAN
MP4	CCMAN
CCD	CCMAN and CCMAN2
CCD(2)	CCMAN
CCSD	CCMAN and CCMAN2
CCSD(T)	CCMAN and CCMAN2
CCSD(2)	CCMAN
CCSD(fT)	CCMAN and CCMAN2
CCSD(dT)	CCMAN
QCISD	CCMAN and CCMAN2
QCISD(T)	CCMAN and CCMAN2
OD	CCMAN
OD(T)	CCMAN
OD(2)	CCMAN
VOD	CCMAN
VOD(2)	CCMAN
QCCD	CCMAN
QCCD(T)	CCMAN
QCCD(2)	CCMAN
VQCCD	CCMAN
VQCCD(T)	CCMAN
VQCCD(2)	CCMAN

$n$	Corresponding to $10^{-n}$ convergence criterion. Amplitude convergence is set
	automatically to match energy convergence.

FALSE	use all integrals in decomposed format
TRUE	transform all RI or Cholesky integral back to conventional format