10.18 Electronic Couplings for Electron Transfer and Energy Transfer

10.18.1 Eigenstate-Based Methods

For electron transfer (ET) and excitation energy transfer (EET) processes, the electronic coupling is one of the important parameters that determine their reaction rates. For ET, Q-Chem provides the coupling values calculated with the generalized Mulliken-Hush (GMH) [558], fragment-charge difference (FCD) [559], Boys localization [560], and Edmiston-Ruedenbeg localization [561] schemes. For EET, options include fragment-excitation difference (FED) [562], fragment-spin difference (FSD) [563], occupied-virtual separated Boys localization [564] or Edmiston-Ruedenberg localization [561]. In all these schemes, a vertical excitation such as CIS, RPA or TDDFT is required, and the GMH, FCD, FED, FSD, Boys or ER coupling values are calculated based on the excited state results.

10.18.1.1 Two-state approximation

Under the two-state approximation, the diabatic reactant and product states are assumed to be a linear combination of the eigenstates. For ET, the choice of such linear combination is determined by a zero transition dipoles (GMH) or maximum charge differences (FCD). In the latter, a 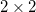$2\times 2$ donor–acceptor charge difference matrix, 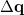$\Delta {\mathbf q}$ , is defined, with elements

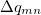	$\displaystyle \label{eq:chargediff} \Delta q_{mn}$	$\displaystyle =$	$\displaystyle q^{\textrm{D}}_{mn} - q^{\textrm{A}}_{mn} \nonumber$
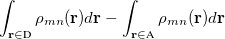	$\displaystyle$	$\displaystyle =$	$\displaystyle \int _{{\mathbf r}\in \textrm{D}} \rho _{mn}({\mathbf r})d{\mathbf r} - \int _{{\mathbf r}\in \textrm{A}} \rho _{mn}({\mathbf r})d{\mathbf r}$		(10.68)

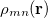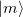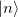where $\rho _{mn}({\mathbf r})$ is the matrix element of the density operator between states $|m\rangle$ and $|n\rangle$ .

For EET, a maximum excitation difference is assumed in the FED, in which a excitation difference matrix is similarly defined with elements

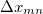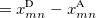	$\displaystyle \label{eq:exdiff} \Delta x_{mn}$	$\displaystyle = x^{\textrm{D}}_{mn} - x^{\textrm{A}}_{mn} \nonumber$
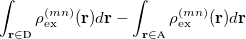	$\displaystyle$	$\displaystyle =$	$\displaystyle \int _{{\mathbf r}\in \textrm{D}} \rho _{\rm ex}^{(mn)}({\mathbf r})d{\mathbf r} - \int _{{\mathbf r}\in \textrm{A}} \rho _{\rm ex}^{(mn)}({\mathbf r})d{\mathbf r}$		(10.69)

where 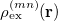$\rho _{\rm ex}^{(mn)}({\mathbf r})$ is the sum of attachment and detachment densities for transition 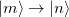$|m\rangle \rightarrow |n\rangle$ , as they correspond to the electron and hole densities in an excitation. In the FSD, a maximum spin difference is used and the corresponding spin difference matrix is defined with its elements as,

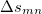	$\displaystyle \label{eq:spindiff} \Delta s_{mn}$	$\displaystyle =$	$\displaystyle s^{\textrm{D}}_{mn} - s^{\textrm{A}}_{mn} \nonumber$
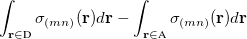	$\displaystyle$	$\displaystyle =$	$\displaystyle \int _{{\mathbf r}\in \textrm{D}} \sigma _{(mn)}({\mathbf r})d{\mathbf r} - \int _{{\mathbf r}\in \textrm{A}} \sigma _{(mn)}({\mathbf r})d{\mathbf r}$		(10.70)

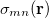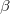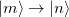where $\sigma _{mn}(\mathbf{r})$ is the spin density, difference between $\alpha$ -spin and $\beta$ -spin densities, for transition from $|m\rangle \rightarrow |n\rangle$ .

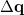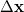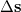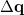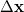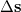Since Q-Chem uses a Mulliken population analysis for the integrations in Eqs. (10.68), (10.69), and (10.70), the matrices $\Delta {\mathbf q}$ , $\Delta {\mathbf x}$ and $\Delta {\mathbf s}$ are not symmetric. To obtain a pair of orthogonal states as the diabatic reactant and product states, $\Delta {\mathbf q}$ , $\Delta {\mathbf x}$ and $\Delta {\mathbf s}$ are symmetrized in Q-Chem. Specifically,

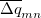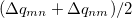$\displaystyle \overline{\Delta q}_{mn}$	$\displaystyle =$	$\displaystyle (\Delta q_{mn}+\Delta q_{nm})/2$	(10.71)
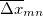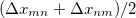$\displaystyle \overline{\Delta x}_{mn}$	$\displaystyle =$	$\displaystyle (\Delta x_{mn}+\Delta x_{nm})/2$	(10.72)
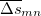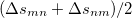$\displaystyle \overline{\Delta s}_{mn}$	$\displaystyle =$	$\displaystyle (\Delta s_{mn}+\Delta s_{nm})/2$	(10.73)

The final coupling values are obtained as listed below:

For GMH,

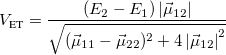
$\begin{equation} V_{\textrm{ET}} = \frac{(E_2 - E_1)\left|\vec\mu _{12}\right|}{\sqrt {(\vec\mu _{11} - \vec\mu _{22})^2 + 4\left|\vec\mu _{12}\right|^{2}}} \end{equation}$ (10.74)
For FCD,

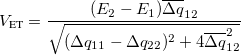
$\begin{equation} V_{\textrm{ET}} = \frac{(E_2 - E_1)\overline{\Delta q}_{12}}{\sqrt {(\Delta q_{11} - \Delta q_{22})^2 + 4\overline{\Delta q}^{2}_{12}}} \end{equation}$ (10.75)
For FED,

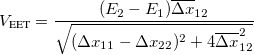
$\begin{equation} V_{\textrm{EET}} = \frac{(E_2 - E_1)\overline{\Delta x}_{12}}{\sqrt {(\Delta x_{11} - \Delta x_{22})^2 + 4\overline{\Delta x}^{2}_{12}}} \end{equation}$ (10.76)
For FSD,

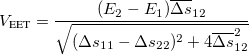
$\begin{equation} V_{\textrm{EET}} = \frac{(E_2 - E_1)\overline{\Delta s}_{12}}{\sqrt {(\Delta s_{11} - \Delta s_{22})^2 + 4\overline{\Delta s}^{2}_{12}}} \end{equation}$ (10.77)

Q-Chem provides the option to control FED, FSD, FCD and GMH calculations after a single-excitation calculation, such as CIS, RPA, TDDFT/TDA and TDDFT. To obtain ET coupling values using GMH (FCD) scheme, one should set $rem variables STS_GMH (STS_FCD) to be TRUE. Similarly, a FED (FSD) calculation is turned on by setting the $rem variable STS_FED (STS_FSD) to be TRUE. In FCD, FED and FSD calculations, the donor and acceptor fragments are defined via the $rem variables STS_DONOR and STS_ACCEPTOR. It is necessary to arrange the atomic order in the $molecule section such that the atoms in the donor (acceptor) fragment is in one consecutive block. The ordering numbers of beginning and ending atoms for the donor and acceptor blocks are included in $rem variables STS_DONOR and STS_ACCEPTOR.

The couplings will be calculated between all choices of excited states with the same spin. In FSD, FCD and GMH calculations, the coupling value between the excited and reference (ground) states will be included, but in FED, the ground state is not included in the analysis. It is important to select excited states properly, according to the distribution of charge or excitation, among other characteristics, such that the coupling obtained can properly describe the electronic coupling of the corresponding process in the two-state approximation.

STS_GMH

Control the calculation of GMH for ET couplings.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not perform a GMH calculation.

TRUE

Include a GMH calculation.

RECOMMENDATION:

When set to true computes Mulliken-Hush electronic couplings. It yields the generalized Mulliken-Hush couplings as well as the transition dipole moments for each pair of excited states and for each excited state with the ground state.

STS_FCD

Control the calculation of FCD for ET couplings.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not perform an FCD calculation.

TRUE

Include an FCD calculation.

RECOMMENDATION:

None

STS_FED

Control the calculation of FED for EET couplings.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not perform a FED calculation.

TRUE

Include a FED calculation.

RECOMMENDATION:

None

STS_FSD

Control the calculation of FSD for EET couplings.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not perform a FSD calculation.

TRUE

Include a FSD calculation.

RECOMMENDATION:

For RCIS triplets, FSD and FED are equivalent. FSD will be automatically switched off and perform a FED calculation.

STS_DONOR

Define the donor fragment.

TYPE:

STRING

DEFAULT:

0

No donor fragment is defined.

OPTIONS:

$i$ - $j$

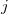
Donor fragment is in the $i$ th atom to the $j$ th atom.

RECOMMENDATION:

Note no space between the hyphen and the numbers $i$ and $j$ .

STS_ACCEPTOR

Define the acceptor molecular fragment.

TYPE:

STRING

DEFAULT:

0

No acceptor fragment is defined.

OPTIONS:

$i$ - $j$

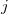
Acceptor fragment is in the $i$ th atom to the $j$ th atom.

RECOMMENDATION:

Note no space between the hyphen and the numbers $i$ and $j$ .

STS_MOM

Control calculation of the transition moments between excited states in the CIS and TDDFT calculations (including SF variants).

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not calculate state-to-state transition moments.

TRUE

Do calculate state-to-state transition moments.

RECOMMENDATION:

When set to true requests the state-to-state dipole transition moments for all pairs of excited states and for each excited state with the ground state.

Example 10.232 A GMH & FCD calculation to analyze electron-transfer couplings in an ethylene and a methaniminium cation.

$molecule
   1  1
   C     0.679952    0.000000    0.000000
   N    -0.600337    0.000000    0.000000
   H     1.210416    0.940723    0.000000
   H     1.210416   -0.940723    0.000000
   H    -1.131897   -0.866630    0.000000
   H    -1.131897    0.866630    0.000000
   C    -5.600337    0.000000    0.000000
   C    -6.937337    0.000000    0.000000
   H    -5.034682    0.927055    0.000000
   H    -5.034682   -0.927055    0.000000
   H    -7.502992   -0.927055    0.000000
   H    -7.502992    0.927055    0.000000
$end

$rem
   METHOD        CIS
   BASIS         6-31+G
   CIS_N_ROOTS   20
   CIS_SINGLETS  true
   CIS_TRIPLETS  false
   STS_GMH       true !turns on the GMH calculation
   STS_FCD       true !turns on the FCD calculation 
   STS_DONOR     1-6  !define the donor fragment as atoms 1-6 for FCD calc.
   STS_ACCEPTOR  7-12 !define the acceptor fragment as atoms 7-12 for FCD calc.
   MEM_STATIC    200  !increase static memory for a CIS job with larger basis set
$end

Example 10.233 An FED calculation to analyze excitation-energy transfer couplings in a pair of stacked ethylenes.

$molecule
   0  1
   C     0.670518    0.000000    0.000000
   H     1.241372    0.927754    0.000000
   H     1.241372   -0.927754    0.000000
   C    -0.670518    0.000000    0.000000
   H    -1.241372   -0.927754    0.000000
   H    -1.241372    0.927754    0.000000
   C     0.774635    0.000000    4.500000
   H     1.323105    0.936763    4.500000
   H     1.323105   -0.936763    4.500000
   C    -0.774635    0.000000    4.500000
   H    -1.323105   -0.936763    4.500000
   H    -1.323105    0.936763    4.500000
$end

$rem
   METHOD            CIS
   BASIS             3-21G
   CIS_N_ROOTS       20
   CIS_SINGLETS      true
   CIS_TRIPLETS      false
   STS_FED           true
   STS_DONOR         1-6
   STS_ACCEPTOR      7-12
$end

10.18.1.2 Multi-state treatments

When dealing with multiple charge or electronic excitation centers, diabatic states can be constructed with Boys [560] or Edmiston-Ruedenberg [561] localization. In this case, we construct diabatic states 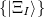$\left\{ \left| \Xi _ I \right> \right\}$ as linear combinations of adiabatic states 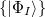$\left\{ \left| \Phi _ I \right> \right\}$ with a general rotation matrix 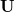$\bf U$ that is 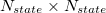$N_{state} \times N_{state}$ in size:

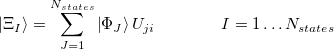$\begin{equation} \label{diabatsum} \left| \Xi _ I \right> = \sum _{J=1}^{N_{states}} \left| \Phi _ J \right> U_{ji} \qquad \qquad I = 1 \ldots N_{states} \end{equation}$

(10.78)

The adiabatic states can be produced with any method, in principle, but the Boys/ER-localized diabatization methods have been implemented thus far only for CIS or TDDFT methods in Q-Chem. In analogy to orbital localization, Boys-localized diabatization corresponds to maximizing the charge separation between diabatic state centers:

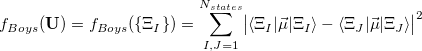$\begin{equation} \label{boysdiabaticsum} f_{Boys}({\bf U}) = f_{Boys}(\{ \Xi _ I\} ) = \sum _{I,J = 1}^{N_{states}} \bigl | \langle \Xi _ I | \vec{\mu } | \Xi _ I \rangle - \langle \Xi _ J | \vec{\mu } | \Xi _ J \rangle \bigl |^2 \end{equation}$

(10.79)

Here, 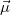$\vec{\mu }$ represents the dipole operator. ER-localized diabatization prescribes maximizing self-interaction energy:

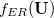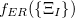	$\displaystyle \label{er2} f_{ER}({\bf U})$	$\displaystyle =$	$\displaystyle f_{ER}( \left\{ \Xi _ I \right\} )$		(10.80)
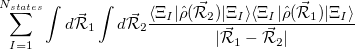	$\displaystyle \nonumber$	$\displaystyle =$	$\displaystyle \sum _{I = 1}^{N_{states}} \int d \mathcal{\vec{R}}_1 \int d \mathcal{\vec{R}}_2 \frac{ \langle \Xi _ I \| \hat{\rho }(\mathcal{\vec{R}}_2) \| \Xi _ I \rangle \langle \Xi _ I \| \hat{\rho }(\mathcal{\vec{R}}_1) \| \Xi _ I \rangle }{\|\mathcal{\vec{R}}_1 - \mathcal{\vec{R}}_2\|}$

where the density operator at position 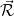$\mathcal{\vec{R}}$ is

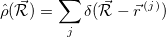$\begin{equation} \hat{\rho }(\mathcal{\vec{R}}) = \sum _ j \delta (\mathcal{\vec{R}} - \vec{r}^{\, (j)}) \end{equation}$

(10.81)

Here, 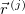$\vec{r}^{\, (j)}$ represents the position of the 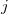$j$ th electron.

These models reflect different assumptions about the interaction of our quantum system with some fictitious external electric field/potential: 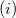$(i)$ if we assume a fictitious field that is linear in space, we arrive at Boys localization; 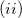$(ii)$ if we assume a fictitious potential energy that responds linearly to the charge density of our system, we arrive at ER localization. Note that in the two-state limit, Boys localized diabatization reduces nearly exactly to GMH [560].

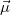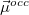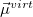As written down in Eq. (10.79), Boys localized diabatization applies only to charge transfer, not to energy transfer. Within the context of CIS or TDDFT calculations, one can easily extend Boys localized diabatization [564] by separately localizing the occupied and virtual components of $\vec{\mu }$ , $\vec{\mu }^{occ}$ and $\vec{\mu }^{virt}$ :

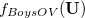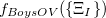	$\displaystyle f_{BoysOV}({\bf U})$	$\displaystyle =$	$\displaystyle f_{BoysOV}(\{ \Xi _ I\} )$		(10.82)
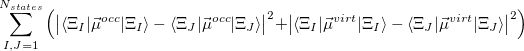	$\displaystyle \nonumber$	$\displaystyle =$	$\displaystyle \sum _{I,J = 1}^{N_{states}} \left( \bigl \| \langle \Xi _ I \| \vec{\mu }^{occ} \| \Xi _ I \rangle - \langle \Xi _ J \| \vec{\mu }^{occ} \| \Xi _ J \rangle \bigl \|^2 + \bigl \| \langle \Xi _ I \| \vec{\mu }^{virt} \| \Xi _ I \rangle - \langle \Xi _ J \| \vec{\mu }^{virt} \| \Xi _ J \rangle \bigr \|^2 \right)$

where

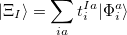$\begin{equation} |\Xi _ I\rangle = \sum _{ia} t_ i^{Ia} | \Phi _ i^ a \rangle \end{equation}$

(10.83)

and the occupied/virtual components are defined by

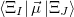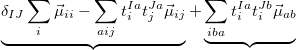	$\displaystyle \left<\Xi _ I\right\| \vec{\mu } \left\|\Xi _ J\right>$	$\displaystyle =$	$\displaystyle \underbrace{\delta _{IJ} \sum _{i} \vec{\mu }_{ii} - \sum _{aij} t^{Ia}_ i t^{Ja}_ j \vec{\mu }_{ij}} +\underbrace{\sum _{iba} t^{Ia}_ i t^{Jb}_ i \vec{\mu }_{ab}}$		(10.84)
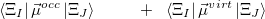	$\displaystyle \nonumber$	$\displaystyle$	$\displaystyle \; \; \; \; \; \; \; \left<\Xi _ I\right\| \vec{\mu }^{occ} \left\|\Xi _ J\right> \; \; \; \; \; \; \; \; \; + \; \; \left<\Xi _ I\right\| \vec{\mu }^{virt} \left\|\Xi _ J\right>$

Note that when we maximize the Boys OV function, we are simply performing Boys-localized diabatization separately on the electron attachment and detachment densities.

Finally, for energy transfer, it can be helpful to understand the origin of the diabatic couplings. To that end, we now provide the ability to decompose the diabatic coupling between diabatic states into into Coulomb (J), Exchange (K) and one-electron (O) components [565]:

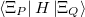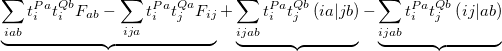	$\displaystyle \nonumber \left< \Xi _ P \right\| H \left\| \Xi _ Q \right>$	$\displaystyle =$	$\displaystyle \underbrace{\sum _{iab} t^{Pa}_ i t^{Qb}_ i F_{ab} - \sum _{ija} t^{Pa}_ i t^{Qa}_ j F_{ij}} + \underbrace{\sum _{ijab} t^{Pa}_ i t^{Qb}_ j \left(ia\|jb\right)} - \underbrace{\sum _{ijab} t^{Pa}_ i t^{Qb}_ j \left(ij\|ab\right)}$
	$\displaystyle$	$\displaystyle$	$\displaystyle \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; O \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; J \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; K$		(10.85)

BOYS_CIS_NUMSTATE

Define how many states to mix with Boys localized diabatization.

TYPE:

INTEGER

DEFAULT:

0

Do not perform Boys localized diabatization.

OPTIONS:

1 to N where N is the number of CIS states requested (CIS_N_ROOTS)

RECOMMENDATION:

It is usually not wise to mix adiabatic states that are separated by more than a few eV or a typical reorganization energy in solvent.

ER_CIS_NUMSTATE

Define how many states to mix with ER localized diabatization.

TYPE:

INTEGER

DEFAULT:

0

Do not perform ER localized diabatization.

OPTIONS:

1 to N where N is the number of CIS states requested (CIS_N_ROOTS)

RECOMMENDATION:

It is usually not wise to mix adiabatic states that are separated by more than a few eV or a typical reorganization energy in solvent.

LOC_CIS_OV_SEPARATE

Decide whether or not to localized the “occupied” and “virtual” components of the localized diabatization function, i.e., whether to localize the electron attachments and detachments separately.

TYPE:

LOGICAL

DEFAULT:

FALSE

Do not separately localize electron attachments and detachments.

OPTIONS:

TRUE

RECOMMENDATION:

If one wants to use Boys localized diabatization for energy transfer (as opposed to electron transfer) , this is a necessary option. ER is more rigorous technique, and does not require this OV feature, but will be somewhat slower.

CIS_DIABATH_DECOMPOSE

Decide whether or not to decompose the diabatic coupling into Coulomb, exchange, and one-electron terms.

TYPE:

LOGICAL

DEFAULT:

FALSE

Do not decompose the diabatic coupling.

OPTIONS:

TRUE

RECOMMENDATION:

These decompositions are most meaningful for electronic excitation transfer processes. Currently, available only for CIS, not for TD-DFT diabatic states.

Example 10.234 A calculation using ER localized diabatization to construct the diabatic Hamiltonian and couplings between a square of singly-excited Helium atoms.

$molecule
0 1
he 0 -1.0 1.0 
he 0 -1.0 -1.0
he 0 1.0 -1.0
he 0 1.0 1.0
$end


$rem
jobtype         sp
method          cis
cis_n_roots     4
cis_singles   false
cis_triplets   true 
basis           6-31g**
scf_convergence 8
symmetry        false
rpa             false
sym_ignore true
sym_ignore true
loc_cis_ov_separate false  ! NOT localizing attachments/detachments separately. 
er_cis_numstate 4          ! using ER to mix 4 adiabatic states.
cis_diabatH_decompose true ! decompose diabatic couplings into 
                           ! Coulomb, exchange, and one-electron components.
$end

$localized_diabatization
On the next line, list which excited adiabatic states we want to mix.
1 2 3 4
$end

10.18.2 Diabatic-State-Based Methods

10.18.2.1 Electronic coupling in charge transfer

A charge transfer involves a change in the electron numbers in a pair of molecular fragments. As an example, we will use the following reaction when necessary, and a generalization to other cases is straightforward:

$\begin{equation} \label{eq:electron-transfer} \mathrm{D}^{-}\mathrm{A} \longrightarrow \mathrm{D}\mathrm{A}^{-} \end{equation}$

(10.86)

where an extra electron is localized to the donor (D) initially, and it becomes localized to the acceptor (A) in the final state. The two-state secular equation for the initial and final electronic states can be written as

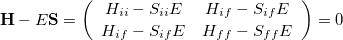$\begin{equation} {\bf H} - E{\bf S} = \left( \begin{array}{cc} H_{ii} - S_{ii}E & H_{if} - S_{if}E \\ H_{if} - S_{if}E & H_{ff} - S_{ff}E \end{array} \right) = 0 \label{eq:2by2HS} \end{equation}$

(10.87)

This is very close to an eigenvalue problem except for the non-orthogonality between the initial and final states. A standard eigenvalue form for Eq. (10.87) can be obtained by using the Löwdin transformation:

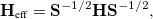$\begin{equation} \mathbf{H}_{\textrm{eff}} =\mathbf{S}^{-1/2}\mathbf{H}\mathbf{S}^{-1/2}, \end{equation}$

(10.88)

where the off-diagonal element of the effective Hamiltonian matrix represents the electronic coupling for the reaction, and it is defined by

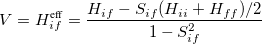$\begin{equation} \label{eq:coupling-normal} V = H^{\textrm{eff}}_{if} = \frac{H_{if} - S_{if}(H_{ii} + H_{ff})/2}{1 - S^{2}_{if}} \end{equation}$

(10.89)

In a general case where the initial and final states are not normalized, the electronic coupling is written as

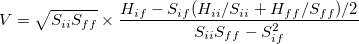$\begin{equation} \label{eq:coupling} V = \sqrt {S_{ii}S_{ff}} \times \frac{H_{if} - S_{if}(H_{ii}/S_{ii} + H_{ff}/S_{ff})/2}{S_{ii}S_{ff} - S^{2}_{if}} \end{equation}$

(10.90)

Thus, in principle, 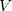$V$ can be obtained when the matrix elements for the Hamiltonian 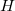$H$ and the overlap matrix 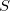$S$ are calculated.

The direct coupling (DC) scheme calculates the electronic coupling values via Eq. (10.90), and it is widely used to calculate the electron transfer coupling [566, 567, 568, 569]. In the DC scheme, the coupling matrix element is calculated directly using charge-localized determinants (the “diabatic states” in electron transfer literatures). In electron transfer systems, it has been shown that such charge-localized states can be approximated by symmetry-broken unrestricted Hartree-Fock (UHF) solutions [566, 567, 570]. The adiabatic eigenstates are assumed to be the symmetric and antisymmetric linear combinations of the two symmetry-broken UHF solutions in a DC calculation. Therefore, DC couplings can be viewed as a result of two-configuration solutions that may recover the non-dynamical correlation.

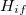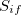The core of the DC method is based on the corresponding orbital transformation [571] and a calculation for Slater’s determinants in $H_{if}$ and $S_{if}$ [568, 569].

10.18.2.2 Corresponding orbital transformation

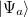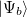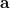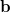Let $|\Psi _{a}\ensuremath{\rangle }$ and $|\Psi _{b}\ensuremath{\rangle }$ be two single Slater-determinant wavefunctions for the initial and final states, and $\ensuremath{\mathbf{a}}$ and $\ensuremath{\mathbf{b}}$ be the spin-orbital sets, respectively:

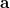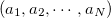	$\displaystyle \ensuremath{\mathbf{a}}$	$\displaystyle =$	$\displaystyle \left(a_1,a_2,\cdots ,a_ N\right)$		(10.91)
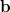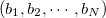	$\displaystyle \ensuremath{\mathbf{b}}$	$\displaystyle =$	$\displaystyle \left(b_1, b_2,\cdots ,b_ N\right)$		(10.92)

Since the two sets of spin-orbitals are not orthogonal, the overlap matrix 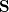$\ensuremath{\mathbf{S}}$ can be defined as:

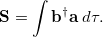$\begin{equation} \ensuremath{\mathbf{S}} = \int \ensuremath{\mathbf{b}}^{\dagger }\ensuremath{\mathbf{a}} \ d\tau . \end{equation}$

(10.93)

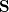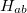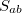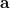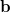We note that $\ensuremath{\mathbf{S}}$ is not Hermitian in general since the molecular orbitals of the initial and final states are separately determined. To calculate the matrix elements $H_{ab}$ and $S_{ab}$ , two sets of new orthogonal spin-orbitals can be used by the corresponding orbital transformation [571]. In this approach, each set of spin-orbitals $\ensuremath{\mathbf{a}}$ and $\ensuremath{\mathbf{b}}$ are linearly transformed,

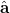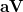	$\displaystyle \hat{\ensuremath{\mathbf{a}}}$	$\displaystyle =$	$\displaystyle \ensuremath{\mathbf{a}}\ensuremath{\mathbf{V}}$		(10.94)
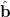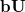	$\displaystyle \hat{\ensuremath{\mathbf{b}}}$	$\displaystyle =$	$\displaystyle \ensuremath{\mathbf{b}}\ensuremath{\mathbf{U}}$		(10.95)

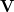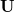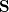where $\ensuremath{\mathbf{V}}$ and $\ensuremath{\mathbf{U}}$ are the left-singular and right-singular matrices, respectively, in the singular value decomposition (SVD) of $\ensuremath{\mathbf{S}}$ :

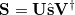$\begin{equation} \ensuremath{\mathbf{S}} = \ensuremath{\mathbf{U}}\hat{\ensuremath{\mathbf{s}}}\ensuremath{\mathbf{V}}^{\dagger } \end{equation}$

(10.96)

The overlap matrix in the new basis is now diagonal

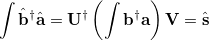$\begin{equation} \int \hat{\ensuremath{\mathbf{b}}}^{\dagger }\hat{\ensuremath{\mathbf{a}}} = \ensuremath{\mathbf{U}}^{\dagger } \left( \int \ensuremath{\mathbf{b}}^{\dagger }\ensuremath{\mathbf{a}} \right) \ensuremath{\mathbf{V}} = \hat{\ensuremath{\mathbf{s}}} \end{equation}$

(10.97)

10.18.2.3 Generalized density matrix

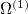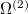The Hamiltonian for electrons in molecules are a sum of one-electron and two-electron operators. In the following, we derive the expressions for the one-electron operator $\Omega ^{(1)}$ and two-electron operator $\Omega ^{(2)}$ ,

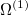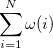	$\displaystyle \Omega ^{(1)}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \omega (i)$		(10.98)
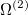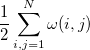	$\displaystyle \Omega ^{(2)}$	$\displaystyle =$	$\displaystyle \frac{1}{2} \sum ^{N}_{i,j=1} \omega (i,j)$		(10.99)

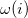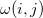where $\omega (i)$ and $\omega (i,j)$ , for the molecular Hamiltonian, are

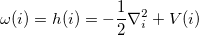$\begin{equation} \omega (i) = h(i) = -\frac{1}{2}\nabla _ i^2 + V(i) \end{equation}$

(10.100)

and

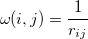$\begin{equation} \omega (i,j) = \frac{1}{r_{ij}} \end{equation}$

(10.101)

The evaluation of matrix elements can now proceed:

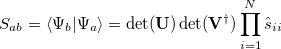$\begin{equation} \label{eq:1par} S_{ab} = \ensuremath{\langle }\Psi _{b} | \Psi _{a} \ensuremath{\rangle }= \det (\ensuremath{\mathbf{U}})\det (\ensuremath{\mathbf{V}}^{\dagger }) \prod _{i=1}^{N} \hat{s}_{ii} \end{equation}$

(10.102)

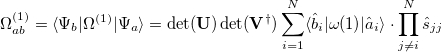$\begin{equation} \Omega ^{(1)}_{ab} = \ensuremath{\langle }\Psi _{b}|\Omega ^{(1)}|\Psi _{a}\ensuremath{\rangle }= \det (\ensuremath{\mathbf{U}})\det (\ensuremath{\mathbf{V}}^{\dagger }) \sum ^{N}_{i=1} \ensuremath{\langle }\hat{b}_{i}|\omega (1)|\hat{a}_{i}\ensuremath{\rangle }\cdot \prod ^{N}_{j\ne i} \hat{s}_{jj} \end{equation}$

(10.103)

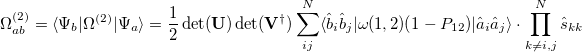$\begin{equation} \label{eq:2par} \Omega ^{(2)}_{ab} = \ensuremath{\langle }\Psi _{b}|\Omega ^{(2)}|\Psi _{a}\ensuremath{\rangle }= \frac{1}{2} \det (\ensuremath{\mathbf{U}})\det (\ensuremath{\mathbf{V}}^{\dagger }) \sum ^{N}_{ij} \ensuremath{\langle }\hat{b}_{i}\hat{b}_{j}|\omega (1,2)(1 -P_{12})|\hat{a}_{i}\hat{a}_{j}\ensuremath{\rangle }\cdot \prod ^{N}_{k\ne {i,j}}\hat{s}_{kk} \end{equation}$

(10.104)

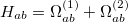$\begin{equation} H_{ab} = \Omega ^{(1)}_{ab} + \Omega ^{(2)}_{ab} \end{equation}$

(10.105)

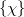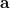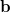In an atomic orbital basis set, $\{ \chi \}$ , we can expand the molecular spin orbitals $\ensuremath{\mathbf{a}}$ and $\ensuremath{\mathbf{b}}$ ,

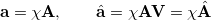	$\displaystyle \ensuremath{\mathbf{a}} = \chi \ensuremath{\mathbf{A}}, \qquad \hat{\ensuremath{\mathbf{a}}} = \chi \ensuremath{\mathbf{A}}\ensuremath{\mathbf{V}} = \chi \hat{\ensuremath{\mathbf{A}}}$		(10.106)
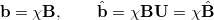	$\displaystyle \ensuremath{\mathbf{b}} = \chi \ensuremath{\mathbf{B}}, \qquad \hat{\ensuremath{\mathbf{b}}} = \chi \ensuremath{\mathbf{B}}\ensuremath{\mathbf{U}} = \chi \hat{\ensuremath{\mathbf{B}}}$		(10.107)

The one-electron terms, Eq. (10.102), can be expressed as

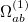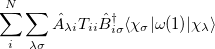	$\displaystyle \Omega ^{(1)}_{ab}$	$\displaystyle =$	$\displaystyle \sum ^{N}_{i}\sum _{\lambda \sigma } \hat{A}_{\lambda i} T_{ii} \hat{B}^{\dagger }_{i \sigma } \ensuremath{\langle }\chi _{\sigma }\|\omega (1)\|\chi _{\lambda }\ensuremath{\rangle }\nonumber$
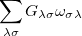	$\displaystyle \label{eq:1par-g}$	$\displaystyle =$	$\displaystyle \sum _{\lambda \sigma } G_{\lambda \sigma }\omega _{\sigma \lambda }$		(10.108)

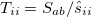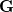where $\displaystyle T_{ii} = S_{ab}/\hat{s}_{ii}$ and define a generalized density matrix, $\ensuremath{\mathbf{G}}$ :

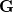$\displaystyle \ensuremath{\mathbf{G}}$

$\displaystyle =$

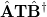$\displaystyle \hat{\ensuremath{\mathbf{A}}}\ensuremath{\mathbf{T}}\hat{\ensuremath{\mathbf{B}}}^{\dagger } \label{eq:g-density}$

(10.109)

Similarly, the two-electron terms [Eq. (10.104)] are

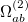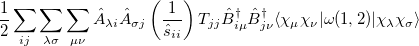	$\displaystyle \Omega ^{(2)}_{ab}$	$\displaystyle =$	$\displaystyle \frac{1}{2}\sum _{ij} \sum _{\lambda \sigma }\sum _{\mu \nu } \hat{A}_{\lambda i}\hat{A}_{\sigma j} \left(\frac{1}{\hat{s}_{ii}}\right)T_{jj} \hat{B}^{\dagger }_{i\mu }\hat{B}^{\dagger }_{j\nu } \ensuremath{\langle }\chi _{\mu }\chi _{\nu }\|\omega (1,2)\|\chi _{\lambda }\chi _{\sigma }\ensuremath{\rangle }\nonumber$
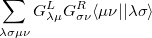	$\displaystyle \label{eq:2par-g}$	$\displaystyle =$	$\displaystyle \sum _{\lambda \sigma \mu \nu } G^{L}_{\lambda \mu }G^{R}_{\sigma \nu }\ensuremath{\langle }\mu \nu \|\|\lambda \sigma \ensuremath{\rangle }$		(10.110)

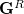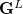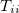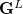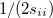where $\ensuremath{\mathbf{G}}^{R}$ and $\ensuremath{\mathbf{G}}^{L}$ are generalized density matrices as defined in Eq. (10.109) except $T_{ii}$ in $\ensuremath{\mathbf{G}}^{L}$ is replaced by $1/(2s_{ii})$ .

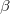The $\alpha$ - and $\beta$ -spin orbitals are treated explicitly. In terms of the spatial orbitals, the one- and two-electron contributions can be reduced to

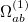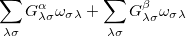$\displaystyle \Omega ^{(1)}_{ab}$	$\displaystyle =$	$\displaystyle \sum _{\lambda \sigma } G^{\alpha }_{\lambda \sigma }\omega _{\sigma \lambda } + \sum _{\lambda \sigma } G^{\beta }_{\lambda \sigma }\omega _{\sigma \lambda } \label{eq:1par-g-ab}$	(10.111)
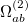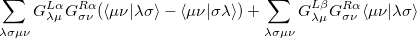$\displaystyle \Omega ^{(2)}_{ab}$	$\displaystyle =$	$\displaystyle \sum _{\lambda \sigma \mu \nu }G^{L\alpha }_{\lambda \mu }G^{R\alpha }_{\sigma \nu } (\ensuremath{\langle }\mu \nu \|\lambda \sigma \ensuremath{\rangle }- \ensuremath{\langle }\mu \nu \|\sigma \lambda \ensuremath{\rangle }) + \sum _{\lambda \sigma \mu \nu }G^{L\beta }_{\lambda \mu }G^{R\alpha }_{\sigma \nu } \ensuremath{\langle }\mu \nu \|\lambda \sigma \ensuremath{\rangle }\nonumber$
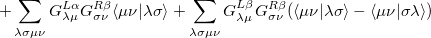$\displaystyle$	$\displaystyle$	$\displaystyle + \sum _{\lambda \sigma \mu \nu }G^{L\alpha }_{\lambda \mu }G^{R\beta }_{\sigma \nu } \ensuremath{\langle }\mu \nu \|\lambda \sigma \ensuremath{\rangle }+ \sum _{\lambda \sigma \mu \nu }G^{L\beta }_{\lambda \mu }G^{R\beta }_{\sigma \nu } (\ensuremath{\langle }\mu \nu \|\lambda \sigma \ensuremath{\rangle }- \ensuremath{\langle }\mu \nu \|\sigma \lambda \ensuremath{\rangle }) \label{eq:2par-g-ab}$	(10.112)

The resulting one- and two-electron contributions, Eqs. (10.111) and (10.112) can be easily computed in terms of generalized density matrices using standard one- and two-electron integral routines in Q-Chem.

10.18.2.4 Direct coupling method for electronic coupling

It is important to obtain proper charge-localized initial and final states for the DC scheme, and this step determines the quality of the coupling values. Q-Chem provides two approaches to construct charge-localized states:

The “1+1” approach
Since the system consists of donor and acceptor molecules or fragments, with a charge being localized either donor or acceptor, it is intuitive to combine wavefunctions of individual donor and acceptor fragments to form a charge-localized wavefunction. We call this approach “1+1” since the zeroth order wavefunctions are composed of the HF wavefunctions of the two fragments.
For example, for the case shown in Example (10.86), we can use Q-Chem to calculate two HF wavefunctions: those of anionic donor and of neutral acceptor and they jointly form the initial state. For the final state, wavefunctions of neutral donor and anionic acceptor are used. Then the coupling value is calculated via Eq. (10.90).
Example 10.235 To calculate the electron-transfer coupling for a pair of stacked-ethylene with “1+1” charge-localized states
```
$molecule
  -1  2
--
  -1  2,  0  1
   C    0.662489    0.000000    0.000000
   H    1.227637    0.917083    0.000000
   H    1.227637   -0.917083    0.000000
   C   -0.662489    0.000000    0.000000
   H   -1.227637   -0.917083    0.000000
   H   -1.227637    0.917083    0.000000
--
   0  1, -1  2
   C    0.720595    0.000000    4.5
   H    1.288664    0.921368    4.5
   H    1.288664   -0.921368    4.5
   C   -0.720595    0.000000    4.5
   H   -1.288664   -0.921368    4.5
   H   -1.288664    0.921368    4.5
$end

$rem
   JOBTYPE               SP
   METHOD                HF
   BASIS                 6-31G(d)
   SCF_PRINT_FRGM        FALSE
   SYM_IGNORE            TRUE
   SCF_GUESS             FRAGMO
   STS_DC                TRUE
$end
```
In the $molecule subsection, the first line is for the charge and multiplicity of the whole system. The following blocks are two inputs for the two molecular fragments (donor and acceptor). In each block the first line consists of the charge and spin multiplicity in the initial state of the corresponding fragment, a comma, then the charge and multiplicity in the final state. Next lines are nuclear species and their positions of the fragment. For example, in the above example, the first block indicates that the electron donor is a doublet ethylene anion initially, and it becomes a singlet neutral species in the final state. The second block is for another ethylene going from a singlet neutral molecule to a doublet anion.
Note that the last three $rem variables in this example, SYM_IGNORE, SCF_GUESS and STS_DC must be set to be the values as in the example in order to perform DC calculation with “1+1” charge-localized states. An additional $rem variable, SCF_PRINT_FRGM is included. When it is TRUE a detailed output for the fragment HF self-consistent field calculation is given.
The “relaxed” approach
In “1+1” approach, the intermolecular interaction is neglected in the initial and final states, and so the final electronic coupling can be underestimated. As a second approach, Q-Chem can use “1+1” wavefunction as an initial guess to look for the charge-localized wavefunction by further HF self-consistent field calculation. This approach would ‘relax’ the wavefunction constructed by “1+1” method and include the intermolecular interaction effects in the initial and final wavefunctions. However, this method may sometimes fail, leading to either convergence problems or a resulting HF wavefunction that cannot represent the desired charge-localized states. This is more likely to be a problem when calculations are performed with with diffusive basis functions, or when the donor and acceptor molecules are very close to each other.
Example 10.236 To calculate the electron-transfer coupling for a pair of stacked-ethylene with “relaxed” charge-localized states
```
$molecule
  -1  2
--
  -1  2,  0  1
   C    0.662489    0.000000    0.000000
   H    1.227637    0.917083    0.000000
   H    1.227637   -0.917083    0.000000
   C   -0.662489    0.000000    0.000000
   H   -1.227637   -0.917083    0.000000
   H   -1.227637    0.917083    0.000000
--
   0  1, -1  2
   C    0.720595    0.000000    4.5
   H    1.288664    0.921368    4.5
   H    1.288664   -0.921368    4.5
   C   -0.720595    0.000000    4.5
   H   -1.288664   -0.921368    4.5
   H   -1.288664    0.921368    4.5
$end

$rem
   JOBTYPE               SP
   METHOD                HF
   BASIS                 6-31G(d)
   SCF_PRINT_FRGM        FALSE
   SYM_IGNORE            TRUE
   SCF_GUESS             FRAGMO
   STS_DC                RELAX
$end
```
To perform ‘relaxed’ DC calculation, set STS_DC to be RELAX.

FALSE	Do not perform a GMH calculation.
TRUE	Include a GMH calculation.

FALSE	Do not perform an FCD calculation.
TRUE	Include an FCD calculation.

FALSE	Do not perform a FED calculation.
TRUE	Include a FED calculation.

FALSE	Do not perform a FSD calculation.
TRUE	Include a FSD calculation.

FALSE	Do not calculate state-to-state transition moments.
TRUE	Do calculate state-to-state transition moments.