10.17 Linear–Scaling Computation of Electric Properties

The search for new optical devices is a major field of materials sciences. Here, polarizabilities and hyperpolarizabilities provide particularly important information on molecular systems. The response of the molecular systems in the presence of an external monochromatic oscillatory electric field is determined by the solution of the TDSCF equations, where the perturbation is represented as the interaction of the molecule with a single Fourier component within the dipole approximation:

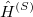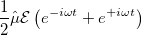	$\displaystyle \hat{H}^{(S)}$	$\displaystyle =$	$\displaystyle \frac{1}{2}\hat{\mu }{\cal {E}}\left(e^{-i\omega t} + e^{+i\omega t}\right)$		(10.66)
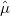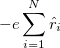	$\displaystyle \hat{\mu }$	$\displaystyle =$	$\displaystyle -e\sum \limits _{i=1}^{N} \hat{r}_{i}$		(10.67)

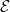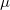Here, $\cal {E}$ is the E-field vector, $\omega$ the corresponding frequency, $e$ the electronic charge and $\mu$ the dipole moment operator. Starting from Frenkel’s variational principle the TDSCF equations can be derived by standard techniques of perturbation theory [556]. As a solution we yield the first ( 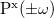$\ensuremath{\mathrm{P}}^{\ensuremath{\mathrm{x}}}(\pm \omega )$ ) and second order (e.g. 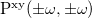$\ensuremath{\mathrm{P}}^{\ensuremath{\mathrm{xy}}}(\pm \omega ,\pm \omega )$ ) perturbed density matrices with which the following properties are calculated:

Static polarizability: $\alpha _{\ensuremath{\mathrm{xy}}}(0;0) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{y}}}\left(\omega =0\right)\right]$
Dynamic polarizability: $\alpha _{\ensuremath{\mathrm{xy}}}(\pm \omega ;\mp \omega ) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{y}}}(\pm \omega )\right]$
Static hyperpolarizability: $\beta _{\ensuremath{\mathrm{xyz}}}(0;0,0) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{yz}}}(\omega =0,\omega =0)\right]$
Second harmonic generation: $\beta _{\ensuremath{\mathrm{xyz}}}(\mp 2\omega ;\pm \omega ,\pm \omega ) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{yz}}}(\pm \omega ,\pm \omega )\right]$
Electro-optical Pockels effect: $\beta _{\ensuremath{\mathrm{xyz}}}(\mp \omega ;0,\pm \omega ) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{yz}}}(\omega =0,\pm \omega )\right]$
Optical rectification: $\beta _{\ensuremath{\mathrm{xyz}}}(0;\pm \omega ,\mp \omega ) = \ensuremath{\mathrm{Tr}}\left[\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{yz}}}(\pm \omega ,\mp \omega )\right]$

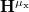where $\ensuremath{\mathbf{H}}^{\mu _{\ensuremath{\mathrm{x}}}}$ is the matrix representation of the $x$ component of the dipole moments.

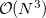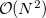
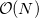The TDSCF calculation is the most time consuming step and scales asymptotically as ${\cal {O}}({N^3})$ because of the AO/MO transformations. The scaling behavior of the two-electron integral formations, which dominate over a wide range because of a larger pre-factor, can be reduced by LinK/CFMM from quadratic to linear ( ${\cal {O}}({N^2})$ $\rightarrow$ ${\cal {O}}({N})$ ).

Third-order properties can be calculated with the equations above after a second-order TDSCF calculation (MOPROP: 101/102) or by use of Wigner’s 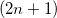$(2n+1)$ rule [557] (MOPROP: 103/104). Since the second order TDSCF depends on the first-order results, the convergence of the algorithm may be problematically. So we recommend the use of 103/104 for the calculation of first hyperpolarizabilities.

These optical properties can be computed for the first time using linear-scaling methods (LinK/CFMM) for all integral contractions [543]. Although the present implementation available in Q-Chem still uses MO-based time-dependent SCF (TDSCF) equations both at the HF and DFT level, the pre-factor of this 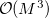${\cal {O}}({M^3})$ scaling step is rather small, so that the reduction of the scaling achieved for the integral contractions is most important. Here, all derivatives are computed analytically.

Further specifications of the dynamic properties are done in the section $fdpfreq in the following format:

$fdpfreq
   property
   frequencies
   units
$end

The first line is only required for third order properties to specify the kind of first hyperpolarizability:

StaticHyper Static Hyperpolarizability
SHG Second harmonic generation
EOPockels Electro-optical Pockels effect
OptRect Optical rectification

Line number 2 contains the values (FLOAT) of the frequencies of the perturbations. Alternatively, for dynamic polarizabilities an equidistant sequence of frequencies can be specified by the keyword WALK (see example below). The last line specifies the units of the given frequencies:

au Frequency (atomic units)
eV Frequency (eV)
nm Wavelength (nm) $\rightarrow$ Note that 0 nm will be treated as 0.0 a.u.
Hz Frequency (Hertz)
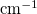cmInv Wavenumber ( $\mathrm{cm}^{-1}$ )

10.17.1 Examples for Section $fdpfreq

Example 10.229 Static and Dynamic polarizabilities, atomic units:

$fdpfreq
   0.0 0.03 0.05
   au
$end

Example 10.230 Series of dynamic polarizabilities, starting with 0.00 incremented by 0.01 up to 0.10:

$fdpfreq
   walk 0.00 0.10 0.01
   au
$end

Example 10.231 Static first hyperpolarizability, second harmonic generation and electro-optical Pockels effect, wavelength in nm:

$fdpfreq
   StaticHyper SHG EOPockels
   1064
   nm
$end

10.17.2 Features of Mopropman

Restricted/unrestricted HF and KS-DFT CPSCF/TDSCF
LinK/CFMM support to evaluate Coulomb- and exchange-like matrices
DIIS acceleration
Support of LSDA/GGA/Hybrid XC functionals listed below
Analytical derivatives

The following XC functionals are supported:

Exchange:

Dirac
Becke 88

Correlation:

Wigner
VWN (both RPA and No. 5 parameterizations)
Perdew-Zunger 81
Perdew 86 (both PZ81 and VWN (No. 5) kernel)
LYP

10.17.3 Job Control

The following options can be used:

MOPROP

Specifies the job for mopropman.

TYPE:

INTEGER

DEFAULT:

0

Do not run mopropman.

OPTIONS:

1

NMR chemical shielding tensors.

2

Static polarizability.

3

Indirect nuclear spin–spin coupling tensors.

100

Dynamic polarizability.

101

First hyperpolarizability.

102

First hyperpolarizability, reading First order results from disk.

103

First hyperpolarizability using Wigner’s $(2n+1)$ rule.

104

First hyperpolarizability using Wigner’s $(2n+1)$ rule, reading

first order results from disk.

RECOMMENDATION:

None

MOPROP_PERTNUM

Set the number of perturbed densities that will to be treated together.

TYPE:

INTEGER

DEFAULT:

0

OPTIONS:

0

All at once.

$n$

Treat the perturbed densities batch-wise.

RECOMMENDATION:

Use default. For large systems, limiting this number may be required to avoid memory exhaustion.

MOPROP_CONV_1ST

Sets the convergence criteria for CPSCF and 1st order TDSCF.

TYPE:

INTEGER

DEFAULT:

6

OPTIONS:

$n<10$

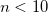
Convergence threshold set to $10^{-n}$ .

RECOMMENDATION:

None

MOPROP_CONV_2ND

Sets the convergence criterion for second-order TDSCF.

TYPE:

INTEGER

DEFAULT:

6

OPTIONS:

$n<10$

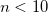
Convergence threshold set to $10^{-n}$ .

RECOMMENDATION:

None

MOPROP_MAXITER_1ST

The maximum number of iterations for CPSCF and first-order TDSCF.

TYPE:

INTEGER

DEFAULT:

50

OPTIONS:

$n$

Set maximum number of iterations to $n$ .

RECOMMENDATION:

Use default.

MOPROP_MAXITER_2ND

The maximum number of iterations for second-order TDSCF.

TYPE:

INTEGER

DEFAULT:

50

OPTIONS:

$n$

Set maximum number of iterations to $n$ .

RECOMMENDATION:

Use default.

MOPROP_ISSC_PRINT_REDUCED

Specifies whether the isotope-independent reduced coupling tensor $\mathbf{K}$ should be printed in addition to the isotope-dependent $\mathbf{J}$ -tensor when calculating indirect nuclear spin–spin couplings.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Do not print $\mathbf{K}$ .

TRUE

Print $\mathbf{K}$ .

RECOMMENDATION:

None

MOPROP_ISSC_SKIP_FC

Specifies whether to skip the calculation of the Fermi contact contribution to the indirect nuclear spin–spin coupling tensor.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Calculate Fermi contact contribution.

TRUE

Skip Fermi contact contribution.

RECOMMENDATION:

None

MOPROP_ISSC_SKIP_SD

Specifies whether to skip the calculation of the spin–dipole contribution to the indirect nuclear spin–spin coupling tensor.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Calculate spin–dipole contribution.

TRUE

Skip spin–dipole contribution.

RECOMMENDATION:

None

MOPROP_ISSC_SKIP_PSO

Specifies whether to skip the calculation of the paramagnetic spin–orbit contribution to the indirect nuclear spin–spin coupling tensor.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Calculate paramagnetic spin–orbit contribution.

TRUE

Skip paramagnetic spin–orbit contribution.

RECOMMENDATION:

None

MOPROP_ISSC_SKIP_DSO

Specifies whether to skip the calculation of the diamagnetic spin–orbit contribution to the indirect nuclear spin–spin coupling tensor.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

FALSE

Calculate diamagnetic spin–orbit contribution.

TRUE

Skip diamagnetic spin–orbit contribution.

RECOMMENDATION:

None

MOPROP_DIIS

Controls the use of Pulay’s DIIS in solving the CPSCF equations.

TYPE:

INTEGER

DEFAULT:

5

OPTIONS:

0

Turn off DIIS.

5

Turn on DIIS.

RECOMMENDATION:

None

MOPROP_DIIS_DIM_SS

Specified the DIIS subspace dimension.

TYPE:

INTEGER

DEFAULT:

20

OPTIONS:

0

No DIIS.

$n$

Use a subspace of dimension $n$ .

RECOMMENDATION:

None

SAVE_LAST_GPX

Save last $\ensuremath{\mathbf{G}}\left[\ensuremath{\mathbf{P}}^{\ensuremath{\mathrm{x}}}\right]$ when calculating dynamic polarizabilities in order to call mopropman in a second run with MOPROP = 102.

TYPE:

INTEGER

DEFAULT:

0

OPTIONS:

0

False

1

True

RECOMMENDATION:

None

1	NMR chemical shielding tensors.
2	Static polarizability.
3	Indirect nuclear spin–spin coupling tensors.
100	Dynamic polarizability.
101	First hyperpolarizability.
102	First hyperpolarizability, reading First order results from disk.
103	First hyperpolarizability using Wigner’s $(2n+1)$ rule.
104	First hyperpolarizability using Wigner’s $(2n+1)$ rule, reading
	first order results from disk.

FALSE	Calculate Fermi contact contribution.
TRUE	Skip Fermi contact contribution.

FALSE	Calculate spin–dipole contribution.
TRUE	Skip spin–dipole contribution.

FALSE	Calculate paramagnetic spin–orbit contribution.
TRUE	Skip paramagnetic spin–orbit contribution.

FALSE	Calculate diamagnetic spin–orbit contribution.
TRUE	Skip diamagnetic spin–orbit contribution.