Q-Chem 5.1 User’s Manual

6.16 Geminal Models

6.16.1 Reference Wave Function

Computational models that use single reference wave function describe molecules in terms of independent electrons interacting via mean Coulomb and exchange fields. It is natural to improve this description by using correlated electron pairs, or geminals, as building blocks for molecular wave functions. Requirements of computational efficiency and size consistency constrain geminals to have 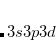$S_{z}=0$,[Rassolov(2002)] with each geminal spanning its own subspace of molecular orbitals.[Arai(1960)] Geminal wave functions were introduced into computational chemistry by Hurley, Lennard-Jones, and Pople.[Hurley et al.(1953)Hurley, Lennard-Jones, and Pople] An excellent review of the history and properties of geminal wave functions is given by Surjan.[Surján(1999)]

We implemented a size consistent model chemistry based on Singlet type Strongly orthogonal Geminals (SSG). In SSG, the number of molecular orbitals in each singlet electron pair is an adjustable parameter chosen to minimize total energy. Open-shell orbitals remain uncorrelated. The SSG wave function is computed by setting SSG $rem variable to 1. Both spin-restricted (RSSG) and spin-unrestricted (USSG) versions are available, chosen by the UNRESTRICTED $rem variable.

The wave function has the form

  $\displaystyle \label{model} \Psi _{\ensuremath{\mathrm{SSG}}} $ $\displaystyle = $ $\displaystyle \hat{A}\left[\psi _1(\ensuremath{\mathbf{r}}_1,\ensuremath{\mathbf{r}}_2) \ldots \psi _{n_{\beta }}(\ensuremath{\mathbf{r}}_{2n_{\beta }-1},\ensuremath{\mathbf{r}}_{2n_{\beta }}) \phi _ i(\ensuremath{\mathbf{r}}_{2n_{\beta }+1}) \ldots \phi _ j(\ensuremath{\mathbf{r}}_{n_{\beta }+n_{\alpha }})\right] $   (6.52)
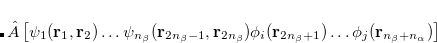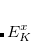  $\displaystyle \psi _ a(\ensuremath{\mathbf{r}}_1,\ensuremath{\mathbf{r}}_2) $ $\displaystyle = $ $\displaystyle \sum _{k\in A}\frac{D^{A}_{i}}{\sqrt {2}} [\phi _{k}({\bf r}_{1})\bar{\phi _{k}}({\bf r}_{2})- \phi _ k(\ensuremath{\mathbf{r}}_2)\bar{\phi _{k}}({\bf r}_{1})] $   (6.53)
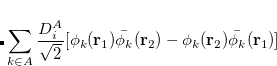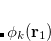  $\displaystyle \phi _ k(\ensuremath{\mathbf{r}}_1) $ $\displaystyle = $ $\displaystyle \sum _{\lambda }C^{k}_{\lambda }\chi _{\lambda }({\bf r}_{1}) $   (6.54)
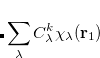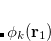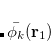  $\displaystyle \bar{\phi _{k}}({\bf r}_{1}) $ $\displaystyle = $ $\displaystyle \sum _{\lambda }\bar{C}^{k}_{\lambda }\chi _{\lambda }({\bf r}_{1}) $   (6.55)

with the coefficients 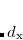$C$, $D$, and subspaces $A$ chosen to minimize the energy

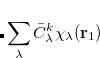  \begin{equation} \label{energy} E_{\ensuremath{\mathrm{SSG}}} = \frac{\langle \Psi _{\ensuremath{\mathrm{SSG}}}|\hat{H}| \Psi _{\ensuremath{\mathrm{SSG}}} \rangle }{ \langle \Psi _{\ensuremath{\mathrm{SSG}}}| \Psi _{\ensuremath{\mathrm{SSG}}} \rangle } \end{equation}   (6.56)

evaluated with the exact Hamiltonian 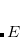$\hat{H}$. A constraint $\bar{C}^{k}_{\lambda }=C^{k}_{\lambda }$ for all MO coefficients yields a spin-restricted version of SSG.

SSG model can use any orbital-based initial guess. It is often advantageous to compute Hartree-Fock orbitals and then read them as initial guess for SSG. The program distinguishes Hartree-Fock and SSG initial guess wave functions, and in former case makes preliminary assignment of individual orbital pairs into geminals. The verification of orbital assignments is performed every ten wave function optimization steps, and the orbital pair is reassigned if total energy is lowered.

The convergence algorithm consists of combination of three types of minimization steps. Direct minimization steps[Seeger and Pople(1976)] seek a minimum along the gradient direction, rescaled by the quantity analogous to the orbital energy differences in SCF theory.[Rassolov(2002)] If the orbitals are nearly degenerate or inverted, a perturbative re-optimization of single geminal is performed. 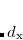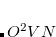Finally, new set of the coefficients $C$ and $D$ is formed from a linear combination of previous iterations, in a manner similar to DIIS algorithm.[Pulay(1980), Pulay(1982)] The size of iterative subspace is controlled by the DIIS_SUBSPACE_SIZE keyword.

After convergence is achieved, SSG reorders geminals based on geminal energy. The energy, along with geminal expansion coefficients, is printed for each geminal. Presence of any but the leading coefficient with large absolute value (value of 0.1 is often used for the definition of “large”) indicates the importance of electron correlation in the system. The Mulliken population analysis is also performed for each geminal, which enables easy assignment of geminals into such chemical objects as core electron pairs, chemical bonds, and lone electron pairs.

As an example, consider the sample calculation of ScH molecule with 6-31G basis set at the experimental bond distance of 1.776 Å. In its singlet ground state the molecule has 11 geminals. Nine of them form core electrons on Sc. Two remaining geminals are:

Geminal 10 E = -1.342609
0.99128 -0.12578 -0.03563 -0.01149 -0.01133 -0.00398

Geminal 11 E = -0.757086
0.96142 -0.17446 -0.16872 -0.12414 -0.03187 -0.01227 -0.01204 -0.00435 -0.00416 -0.00098

Mulliken population analysis shows that geminal 10 is delocalized between Sc and H, indicating a bond. It is moderately correlated, with second expansion coefficient of a magnitude 0.126. The geminal of highest energy is localized on Sc. It represents 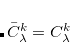$4s^2$ electrons and describes their excitation into $3d$ orbitals. Presence of three large expansion coefficients show that this effect cannot be described within GVB framework.[Bobrowicz and Goddard III(1977)]

6.16.2 Perturbative Corrections

The SSG description of molecular electronic structure can be improved by perturbative description of missing inter-geminal correlation effects. We have implemented Epstein-Nesbet form of perturbation theory[Epstein(1926), Nesbet(1955)] that permits a balanced description of one- and two-electron contributions to excited states’ energies in SSG model. This form of perturbation theory is especially accurate for calculation of weak intermolecular forces. Also, two-electron $[i\bar{j},j\bar{i}]$ integrals are included in the reference Hamiltonian in addition to intra-geminal $[i\bar{j},i\bar{j}]$ integrals that are needed for reference wave function to be an eigenfunction of the reference Hamiltonian.[Rassolov et al.(2004)Rassolov, Xu, and Garaschchuk]

All perturbative contributions to the SSG(EN2) energy (second-order Epstein-Nesbet perturbation theory of SSG wave function) are analyzed in terms of largest numerators, smallest denominators, and total energy contributions by the type of excitation. All excited states are subdivided into dispersion-like with correlated excitation within one geminal coupled to the excitation within another geminal, single, and double electron charge transfer. This analysis permits careful assessment of the quality of SSG reference wave function. Formally, the SSG(EN2) correction can be applied both to RSSG and USSG wave functions. Experience shows that molecules with broken or nearly broken bonds may have divergent RSSG(EN2) corrections. USSG(EN2) theory is balanced, with largest perturbative corrections to the wave function rarely exceeding 0.1 in magnitude.

SSG

Controls the calculation of the SSG wave function.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Do not compute the SSG wave function

1

Do compute the SSG wave function


RECOMMENDATION:

See also the UNRESTRICTED and DIIS_SUBSPACE_SIZE $rem variables.