6.4 Exact MP2 Methods
6.4.1 Algorithm
Second-order Møller-Plesset theory[Møller and Plesset(1934)] (MP2) is probably the simplest useful wave function-based electron correlation method. Revived in the mid-1970s, it remains highly popular today, because it offers systematic improvement in optimized geometries and other molecular properties relative to Hartree-Fock (HF) theory.[Hehre et al.(1986)Hehre, Radom, v. R. Schleyer, and Pople] Indeed, in a recent comparative study of small closed-shell molecules,[Helgaker et al.(1997)Helgaker, Gauss, Jorgensen, and Olsen] MP2 outperformed much more expensive singles and doubles coupled-cluster theory for such properties! Relative to state-of-the-art Kohn-Sham density functional theory (DFT) methods, which are the most economical methods to account for electron correlation effects, MP2 has the advantage of properly incorporating long-range dispersion forces. The principal weaknesses of MP2 theory are for open shell systems, and other cases where the HF determinant is a poor starting point.
Q-Chem contains an efficient conventional semi-direct method to evaluate the MP2 energy and gradient.[Head-Gordon(1999)] These methods require  memory (
memory (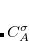 ,
,  ,
,  are the numbers of occupied, virtual and total orbitals, respectively), and disk space which is bounded from above by
are the numbers of occupied, virtual and total orbitals, respectively), and disk space which is bounded from above by 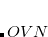 . The latter can be reduced to
. The latter can be reduced to 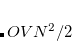 by treating the occupied orbitals in batches of size
by treating the occupied orbitals in batches of size 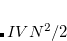 , and re-evaluating the two-electron integrals
, and re-evaluating the two-electron integrals  times. This approach is tractable on modern workstations for energy and gradient calculations of at least 500 basis functions or so, or molecules of between 15 and 30 first row atoms, depending on the basis set size. The computational cost increases between the 3rd and 5th power of the size of the molecule, depending on which part of the calculation is time-dominant.
times. This approach is tractable on modern workstations for energy and gradient calculations of at least 500 basis functions or so, or molecules of between 15 and 30 first row atoms, depending on the basis set size. The computational cost increases between the 3rd and 5th power of the size of the molecule, depending on which part of the calculation is time-dominant.
The algorithm and implementation in Q-Chem is improved over earlier methods,[Head-Gordon et al.(1988)Head-Gordon, Pople, and Frisch, Frisch et al.(1990)Frisch, Head-Gordon, and Pople] particularly in the following areas:
Uses pure functions, as opposed to Cartesians, for all fifth-order steps. This leads to large computational savings for basis sets containing pure functions.
Customized loop unrolling for improved efficiency.
The sort-less semi-direct method avoids a read and write operation resulting in a large I/O savings.
Reduction in disk and memory usage.
No extra integral evaluation for gradient calculations.
Full exploitation of frozen core approximation.
The implementation offers the user the following alternatives:
Direct algorithm (energies only).
Disk-based sort-less semi-direct algorithm (energies and gradients).
Local occupied orbital method (energies only).
The semi-direct algorithm is the only choice for gradient calculations. It is also normally the most efficient choice for energy calculations. There are two classes of exceptions:
If the amount of disk space available is not significantly larger than the amount of memory available, then the direct algorithm is preferred.
If the calculation involves a very large basis set, then the local orbital method may be faster, because it performs the transformation in a different order. It does not have the large memory requirement (no
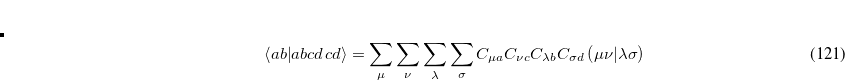 array needed), and always evaluates the integrals four times. The AO2MO_DISK option is also ignored in this algorithm, which requires up to
array needed), and always evaluates the integrals four times. The AO2MO_DISK option is also ignored in this algorithm, which requires up to 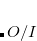 megabytes of disk space.
megabytes of disk space.
There are three important options that should be wisely chosen by the user in order to exploit the full efficiency of Q-Chem’s direct and semi-direct MP2 methods (as discussed above, the LOCAL_OCCUPIED method has different requirements).
MEM_STATIC: The value specified for this $rem variable must be sufficient to permit efficient integral evaluation (10-80Mb) and to hold a large temporary array whose size is
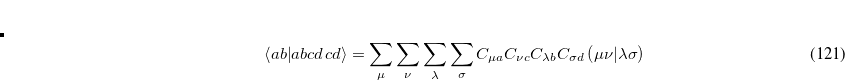 , the product of the number of occupied, virtual and total numbers of orbitals.
, the product of the number of occupied, virtual and total numbers of orbitals. AO2MO_DISK: The value specified for this $rem variable should be as large as possible (i.e., perhaps 80% of the free space on your $QCSCRATCH partition where temporary job files are held). The value of this variable will determine how many times the two-electron integrals in the atomic orbital basis must be re-evaluated, which is a major computational step in MP2 calculations.
N_FROZEN_CORE: The computational requirements for MP2 are proportional to the number of occupied orbitals for some steps, and the square of that number for other steps. Therefore the CPU time can be significantly reduced if your job employs the frozen core approximation. Additionally the memory and disk requirements are reduced when the frozen core approximation is employed.
6.4.2 Algorithm Control and Customization
The direct and semi-direct integral transformation algorithms used by Q-Chem (e.g., MP2, CIS(D)) are limited by available disk space, 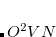 , and memory,
, and memory, 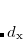 , the number of basis functions,
, the number of basis functions,  , the number of virtual orbitals,
, the number of virtual orbitals, 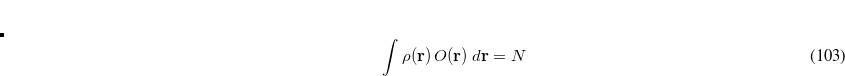 and the number of occupied orbitals,
and the number of occupied orbitals, 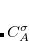 , as discussed above. The generic description of the key $rem variables are:
, as discussed above. The generic description of the key $rem variables are:
MEM_STATIC
Sets the memory for Fortran AO integral calculation and transformation modules.
TYPE:
INTEGER
DEFAULT:
64
corresponding to 64 Mb.
OPTIONS:

User-defined number of megabytes.
RECOMMENDATION:
For direct and semi-direct MP2 calculations, this must exceed OVN + requirements for AO integral evaluation (32–160 Mb), as discussed above.
MEM_TOTAL
Sets the total memory available to Q-Chem, in megabytes.
TYPE:
INTEGER
DEFAULT:
2000
Corresponding to 2000 Mb.
OPTIONS:

User-defined number of megabytes.
RECOMMENDATION:
Use the default, or set equal to the physical memory of your machine. Note that if the memory allocation total more than 1 Gb for a CCMAN job, the memory is allocated as follows
12%
MEM_STATIC
50%
CC_MEMORY
35%
Other memory requirements:
AO2MO_DISK
Sets the amount of disk space (in megabytes) available for MP2 calculations.
TYPE:
INTEGER
DEFAULT:
2000
Corresponding to 2000 Mb.
OPTIONS:

User-defined number of megabytes.
RECOMMENDATION:
Should be set as large as possible, discussed in Section 6.4.1.
CD_ALGORITHM
Determines the algorithm for MP2 integral transformations.
TYPE:
STRING
DEFAULT:
Program determined.
OPTIONS:
DIRECT
Uses fully direct algorithm (energies only).
SEMI_DIRECT
Uses disk-based semi-direct algorithm.
LOCAL_OCCUPIED
Alternative energy algorithm (see 6.4.1).
RECOMMENDATION:
Semi-direct is usually most efficient, and will normally be chosen by default.
6.4.3 Example
Example 6.69 Example of an MP2/6-31G* calculation employing the frozen core approximation. Note that the EXCHANGE $rem variable will default to HF
$molecule
0 1
O
H1 O oh
H2 O oh H1 hoh
oh = 1.01
hoh = 105
$end
$rem
METHOD mp2
BASIS 6-31g*
N_FROZEN_CORE fc
$end