12.7 Frozen-Density Embedding Theory based methods

Frozen-Density Embedding Theory[Wesolowski and Warshel(1993), Wesolowski(2008)] (FDET) provides a formal framework in which the whole system is described by means of two independent quantities: the embedded wave function (interacting or not) and the density associated with the environment. The total energy equation in frozen density embedding theory for a wave function in state 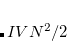$I$ embedded in a environment density $\rho _{B}^{}$ reads (for definitions see Table 12.8):

	$\displaystyle \label{eq:fdet_ conv} E_{AB}^\ensuremath{\mathrm{}}{tot}[\Psi _{A}^{I},\rho _{B}^{}]$	$\displaystyle = \langle \Psi _{A}^{I} \| \hat{H}_{A}^{} \| \Psi _{A}^{I} \rangle + V_{B}^\ensuremath{\mathrm{}}{nuc}[\rho _{A}^{I}] + J_\ensuremath{\mathrm{}}{int}^{}[\rho _{A}^{I},\rho _{B}^{}] + E_{xc}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}]$		(12.91)
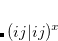	$\displaystyle$	$\displaystyle \quad + T_{s}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}] + E_{v_{B}}^\ensuremath{\mathrm{}}{HK}[\rho _{B}^{}] + V_{A}^\ensuremath{\mathrm{}}{nuc}[\rho _{B}^{}]$		(12.92)

The embedding operator $\hat{v}_\ensuremath{\mathrm{}}{emb}$ , which is added to the Hamiltonian of subsystem A $\left(\hat{H}_{A}^{}\right)$ , is given in the form of a potential:

$\begin{equation} \label{eq:fdet_ vemb} v_\ensuremath{\mathrm{}}{emb}^{}[\rho _{A}^{I}, \rho _{B}^{}, v_{B}^{}](\mathbf{r}) = v_{B}^{}(\mathbf{r}) + \int \frac{\rho _{B}^{}(\mathbf{r}')}{| \mathbf{r}-\mathbf{r}'|}\mathrm{d}\mathbf{r} + \frac{\delta E_{xc,T}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}]}{\delta \rho _{A}^{I}(\mathbf{r})} \end{equation}$

(12.93)

The last term (non-electrostatic component) in equation causes the embedding potential to be $\rho _{A}^{}$ -dependent, which in return induces an inconsistency between the potential and the energy. In the canonical form of FDET (conventional FDET) this inconsistency is addressed by performing macrocycles in which the embedding potential is repeatedly constructed using the current (embedded) density $\rho _{A}^\ensuremath{\mathrm{}}{curr}(\mathbf{r})$ after each cycle until self-consistency is reached.

In linearized FDET the non-additive energy functionals (for abbreviation denoted as $E_{xc,T}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}]$ ) are each approximated by a functional which is linear in $\rho _{A}^{}(\mathbf{r})$ . The approximation is constructed as a Taylor expansion of the non-additive energy functional at a reference density $\rho _{A}^\ensuremath{\mathrm{}}{ref}(\mathbf{r})$ with the series being truncated after the linear term.

$\begin{equation} \label{eq:fdet_ lin} E_{xc,T}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}] \approx E_{xc,T}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^\ensuremath{\mathrm{}}{ref}, \rho _{B}^{}] + \int \left( \rho _{A}^{I}(\mathbf{r}) - \rho _{A}^\ensuremath{\mathrm{}}{ref}(\mathbf{r}) \right) \frac{\delta E_{xc,T}^{nad}[\rho _{A}^\ensuremath{\mathrm{}}{ref}, \rho _{B}^{}]}{\delta \rho _{A}^\ensuremath{\mathrm{}}{ref}(\mathbf{r})} \mathrm{d}\mathbf{r} \end{equation}$

(12.94)

In contrast to conventional FDET, the embedding potential then becomes $\rho _{A}^{}$ -independent and macrocycles are no longer necessary. Another consequence of the linearization is that orthogonality between states is maintained since the same potential is used for all states.

12.7.1 FDE-ADC

FDE-ADC[Prager et al.(2016)Prager, Zech, Aquilante, Dreuw, and Wesolowski] is a density embedding method based on the combination of the Algebraic Diagrammatic Construction scheme for the polarization propagator (ADC, Section 7.8) and Frozen-Density Embedding Theory (FDET). In this particular variant the subsystem A is represented by a wave function whereas subsystem B is described by a density. The FDE-ADC method uses the linearized FDET approximation.[Zech et al.(2015)Zech, Aquilante, and Wesolowski]

12.7.1.1 FDE-ADC Job Control

The FDE-ADC job control is accomplished in two sections, $rem and $fde. Enabling FDE-ADC, specification of the ADC method and other ADC job control parameters (thresholds, max. iterations etc.) should be set in the $rem section. FDE-ADC also supports the excited state analysis (STATE_ANALYSIS) carried out by the libwfa module.

The fragments are specified via the fragment descriptors (see Section 13) in the $molecule section, whereas the first fragment corresponds to the embedded species (A) while the second fragment represents the environment (B).

Note: The current implementation allows only for closed shell fragments.

FDE

Turns density embedding on.

TYPE:

BOOLEAN

DEFAULT:

False

OPTIONS:

True

Perform an FDE-ADC calculation.

False

Don’t perform FDE-ADC calculation.

RECOMMENDATION:

Set the $rem variable FDE to TRUE to start a FDE-ADC calculation.

METHOD

Determines which FDE-ADC method should be used if FDE = True.

TYPE:

STRING

DEFAULT:

None

OPTIONS:

adc(2)

Perform an FDE-ADC(2)-s calculation.

adc(2)-x

Perform an FDE-ADC(2)-x calculation.

adc(3)

Perform an FDE-ADC(3) calculation (potential constructed with MP(2) density).

cvs-adc(2)

Perform an FDE-ADC(2)-s calculation of core excitations.

cvs-adc(2)-x

Perform an FDE-ADC(2)-x calculation of core excitations.

cvs-adc(3)

Perform an FDE-ADC(3) calculation of core excitations.

RECOMMENDATION:

None

The FDE-ADC job control with respect to embedding parameters is accomplished via options in the $fde input section. The format of the $fde section requires key and value pairs separated by a space character:

$fde
   <Keyword>  <parameter>
$end

Note: The following job control variables belong only in the $fde section. Do not place them in the $rem section.

The super-molecular expansion (SE) uses the full basis set of the super-system for calculations on each fragment. Because of the computational cost this option should only be used for small to medium sized super-systems. Note that for visualization of orbitals or densities SE only supports the generation of volumetric data via MAKE_CUBE_FILES (MolDen files are not supported, i.e. MOLDEN_FORMAT should be avoided).

The reassembling of density matrix[Prager et al.(2016)Prager, Zech, Aquilante, Dreuw, and Wesolowski] (RADM) option allows for calculations on larger systems by only including the basis functions of the embedded species for the ADC calculation. RADM introduces an approximation for the construction of the embedding potential by using an artificially (but cheaply) constructed density matrix for subsystem A. With RADM, all regular options for visualization are supported (MAKE_CUBE_FILES and MOLDEN_FORMAT). The RADM option is the recommended choice for an FDE-ADC calculation.

Analogous to a regular DFT calculation in Q-Chem(by using METHOD) the exchange-correlation functional combination can either be selected with one keyword XC_Func,or by defining X_Func and C_Func (similar to EXCHANGE and CORRELATION).

T_Func

Kinetic energy functional used for the construction of the embedding potential.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

TF

Use Thomas-Fermi kinetic energy functional.

RECOMMENDATION:

None

XC_Func

Exchange-Correlation functional used for the construction of the embedding potential.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA exchange-correlation functionals available in Q-Chem.

RECOMMENDATION:

Only use LDA or GGA-type functionals.

X_Func

Exchange functional used for the construction of the embedding potential.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA exchange functionals available in Q-Chem.

RECOMMENDATION:

Only use LDA or GGA-type functionals. XC_Func and X_Func are mutually exclusive.

C_Func

Exchange-Correlation functional used for the construction of the embedding potential.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA correlation functionals available in Q-Chem.

RECOMMENDATION:

Only use LDA or GGA-type functionals. XC_Func and C_Func are mutually exclusive.

Expansion

Specifies which basis set expansion should be used.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

SE/super/supermolecular

Supermolecular basis is used for both System A and B.

RADM

Use RADM approximation (see above).

RECOMMENDATION:

SE should be used for testing purposes only since it is very expensive for large systems. Use the RADM approximation for larger systems.

rhoB_method

Method to calculate the environment density (B).

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

HF

Use Hartree-Fock method.

DFT

Use Density Functional Theory.

RECOMMENDATION:

If DFT is specified, the respective exchange-correlation functional has to defined using the keyword XC_FUNC_B or X_FUNC_B and C_FUNC_B.

XC_Func_B

Exchange-Correlation functional used for the environment DFT calculation.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA/global-hybrid-GGA exchange-correlation functionals available in Q-Chem.

RECOMMENDATION:

None

X_Func_B

Exchange functional used for the environment DFT calculation.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA exchange functionals available in Q-Chem.

RECOMMENDATION:

XC_Func_B and X_Func_B are mutually exclusive.

C_Func_B

Correlation functional used for the environment DFT calculation.

INPUT SECTION: $fde
TYPE:

STRING

DEFAULT:

None

OPTIONS:

All LDA/GGA correlation functionals available in Q-Chem.

RECOMMENDATION:

XC_Func_B and C_Func_B are mutually exclusive.

PrintLevel

Print level for FDE-ADC output.

INPUT SECTION: $fde
TYPE:

INTEGER

DEFAULT:

0

OPTIONS:

0

minimum print level

1

extended print level

2

maximum print level

3

max. print level and additional text files (densities, etc.)

RECOMMENDATION:

None

12.7.1.2 Examples

Example 12.310 Input for a FDE-ADC(2)/cc-pVDZ calculation in supermolecular expansion on CO embedded in one water molecule.

$rem
   SYM_IGNORE           = true
   METHOD               = adc(2)
   EE_STATES            = 2
   BASIS                = cc-pvdz
   FDE                  = true
   MEM_STATIC           = 1024
   MEM_TOTAL            = 16000
   ADC_DAVIDSON_MAXITER = 100
   ADC_DAVIDSON_CONV    = 5
$end

$molecule
   0 1
--
   0 1
   C    -3.618090    1.376803   -0.020795
   O    -4.735683    1.525556    0.115023
--
   0 1
   O    -7.956372    1.485406    0.116792
   H    -6.992316    1.421133    0.177470
   H    -8.105846    2.442220    0.111599
$end

$fde
   T_Func       TF
   XC_Func      PBE
   expansion    super
   rhoB_method  HF
$end

12.7.1.3 FDE-ADC output

In general the FDE-ADC output indicates all important stages of the FDE-ADC calculation, which are:

Generation of $\rho _{A}^\ensuremath{\mathrm{}}{ref}$ ,
Generation of $\rho _{B}^{}$ ,
Construction of the embedding potential,
Start of FDE-ADC calculation and
Final FDE-ADC summary.

In the following table definitions of the terms printed to the output are collected. These quantities are printed for every state, i.e. for every $\rho _{A}^{I}(\mathbf{r})$ . In addition, the non-electrostatic interactions with respect to the reference density $\rho _{A}^\ensuremath{\mathrm{}}{ref}(\mathbf{r})$ are printed at the top of the FDE-ADC summary.

Subsystem Energies
`Embedded system (A)`	$\langle \Psi _{A}^{I} \| \hat{H}_{A} + v_\ensuremath{\mathrm{}}{emb}^\ensuremath{\mathrm{}}{lin} \| \Psi _{A}^{I}\rangle$
`Environment (B)`	$E_{B}^{} = E_{v_{B}}^\ensuremath{\mathrm{}}{HK}[\rho _{B}^{}]\; \text {or}\; E_\ensuremath{\mathrm{}}{HF}$
Electrostatic Interactions
`rho_A <-> rho_B`	$J_\ensuremath{\mathrm{}}{int}^{}[\rho _{A}^{},\rho _{B}^{}] = \int \int \frac{\rho _{A}^{}(\mathbf{r})\rho _{B}^{}(\mathbf{r}')}{\|\mathbf{r}-\mathbf{r}'\|} \mathrm{d}\mathbf{r}\mathrm{d}\mathbf{r}’$
`rho_A <-> Nuc_B`	$V_{B}^\ensuremath{\mathrm{}}{nuc}[\rho _{A}^{}] = \int \rho _{A}^{}(\mathbf{r})v_{B}^{}(\mathbf{r})\mathrm{d}\mathbf{r}$
`rho_B <-> Nuc_A`	$V_{A}^\ensuremath{\mathrm{}}{nuc}[\rho _{B}^{}] = \int \rho _{B}^{}(\mathbf{r})v_{A}^{}(\mathbf{r})\mathrm{d}\mathbf{r}$
`Nuc_A <-> Nuc_B`	$V_{N_{A}N_{B}} = \sum _{i}\sum _{j} \frac{Z_{i}^{}Z_{j}^{}}{\|R_{i}^{}-R_{j}^{}\|}$
Non-Electrostatic Interactions
`non-additive E_xc`	$E_{xc}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}]$
`non-additive T_s`	$T_{s}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^{I},\rho _{B}^{}]$
`integrated v_xc nad`	$\int \rho _{A}^{I}(\mathbf{r})v_{xc}^\ensuremath{\mathrm{}}{nad}(\mathbf{r})\mathrm{d}\mathbf{r}$
`integrated v_T nad`	$\int \rho _{A}^{I}(\mathbf{r})v_{T}^\ensuremath{\mathrm{}}{nad}(\mathbf{r})\mathrm{d}\mathbf{r}$
Final FDE-ADC energies
`Delta_Lin`	$\int ( \rho _{A}^{I}(\mathbf{r}) - \rho _{A}^\ensuremath{\mathrm{}}{ref}(\mathbf{r}))v_{xc,T}^\ensuremath{\mathrm{}}{nad}(\mathbf{r})\mathrm{d}\mathbf{r}$
`Final Energy (A)`	$E_{A}^\ensuremath{\mathrm{}}{emb}[\Psi _{A}^{I},\rho _{B}^{}] = \langle \Psi _{A}^{I} \| \hat{H}_{A} \| \Psi _{A}^{I}\rangle + J_\ensuremath{\mathrm{}}{int}^{}[\rho _{A}^{I},\rho _{B}^{}] + V_{B}^\ensuremath{\mathrm{}}{nuc}[\rho _{A}^{I}]$
	$+ E_{xc,T}^\ensuremath{\mathrm{}}{nad}[\rho _{A}^\ensuremath{\mathrm{}}{ref},\rho _{B}] + \Delta ^\ensuremath{\mathrm{}}{lin}[\rho _{A}^{I},\rho _{A}^\ensuremath{\mathrm{}}{ref},\rho _{B}^{}] + V_{A}^\ensuremath{\mathrm{}}{nuc}[\rho _{B}^{}] + V_{N_{A}N_{B}}$
`Final Energy (A+B)`	$E_{A}^\ensuremath{\mathrm{}}{emb}[\Psi _{A}^{I},\rho _{B}^{}] + E_{B}$

Table 12.8: Definition of output terms.

True	Perform an FDE-ADC calculation.
False	Don’t perform FDE-ADC calculation.

adc(2)	Perform an FDE-ADC(2)-s calculation.
adc(2)-x	Perform an FDE-ADC(2)-x calculation.
adc(3)	Perform an FDE-ADC(3) calculation (potential constructed with MP(2) density).
cvs-adc(2)	Perform an FDE-ADC(2)-s calculation of core excitations.
cvs-adc(2)-x	Perform an FDE-ADC(2)-x calculation of core excitations.
cvs-adc(3)	Perform an FDE-ADC(3) calculation of core excitations.

SE/super/supermolecular	Supermolecular basis is used for both System A and B.
RADM	Use RADM approximation (see above).

0	minimum print level
1	extended print level
2	maximum print level
3	max. print level and additional text files (densities, etc.)