Q-Chem 5.1 User’s Manual

11.10 Harmonic Vibrational Analysis

Vibrational analysis is an extremely important tool for the quantum chemist, supplying a molecular fingerprint which is invaluable for aiding identification of molecular species in many experimental studies. Q-Chem includes a vibrational analysis package that can calculate vibrational frequencies and their Raman[Johnson and Florián(1995)] and infrared activities. Vibrational frequencies are calculated by either using an analytic Hessian (if available; see Table 10.1) or, numerical finite difference of the gradient. The default setting in Q-Chem is to use the highest analytical derivative order available for the requested theoretical method.

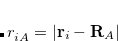When calculating analytic frequencies at the HF and DFT levels of theory, the coupled-perturbed SCF equations must be solved. This is the most time-consuming step in the calculation, and also consumes the most memory. The amount of memory required is $\mbox{${\cal {O}}({N^2M})$}$ where $N$ is the number of basis functions, and $M$ the number of atoms. This is an order more memory than is required for the SCF calculation, and is often the limiting consideration when treating larger systems analytically. Q-Chem incorporates a new approach to this problem that avoids this memory bottleneck by solving the CPSCF equations in segments.[Korambath et al.(2002)Korambath, Kong, Furlani, and Head-Gordon] Instead of solving for all the perturbations at once, they are divided into several segments, and the CPSCF is applied for one segment at a time, resulting in a memory scaling of $\mbox{${\cal {O}}({N^2M/N_{\ensuremath{\mathrm{seg}}}})$}$, where $N_{\ensuremath{\mathrm{seg}}}$ is the number of segments. This option is invoked automatically by the program.

Following a vibrational analysis, Q-Chem computes useful statistical thermodynamic properties at standard temperature and pressure, including: zero-point vibration energy (ZPVE) and, translational, rotational and vibrational, entropies and enthalpies.

The performance of various ab initio theories in determining vibrational frequencies has been well documented; see Refs. Murray:1992,Scott:1996,Johnson:1993d.

11.10.1 Job Control

In order to carry out a frequency analysis users must at a minimum provide a molecule within the $molecule keyword and define an appropriate level of theory within the $rem keyword using the $rem variables EXCHANGE, CORRELATION (if required) (Chapter 4) and BASIS (Chapter 8). Since the default type of job (JOBTYPE) is a single point energy (SP) calculation, the JOBTYPE $rem variable must be set to FREQ.

It is very important to note that a vibrational frequency analysis must be performed at a stationary point on the potential surface that has been optimized at the same level of theory. Therefore a vibrational frequency analysis most naturally follows a geometry optimization in the same input deck, where the molecular geometry is obtained (see examples).

Users should also be aware that the quality of the quadrature grid used in DFT calculations is more important when calculating second derivatives. The default grid for some atoms has changed in Q-Chem 3.0 (see Section 5.5) and for this reason vibrational frequencies may vary slightly form previous versions. It is recommended that a grid larger than the default grid is used when performing frequency calculations.

The standard output from a frequency analysis includes the following.

Several other $rem variables are available that control the vibrational frequency analysis. In detail, they are:

DORAMAN

Controls calculation of Raman intensities. Requires JOBTYPE to be set to FREQ


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Do not calculate Raman intensities.

TRUE

Do calculate Raman intensities.


RECOMMENDATION:

None


VIBMAN_PRINT

Controls level of extra print out for vibrational analysis.


TYPE:

INTEGER


DEFAULT:

1


OPTIONS:

1

Standard full information print out.

 

If VCI is TRUE, overtones and combination bands are also printed.

3

Level 1 plus vibrational frequencies in atomic units.

4

Level 3 plus mass-weighted Hessian matrix, projected mass-weighted Hessian

 

matrix.

6

Level 4 plus vectors for translations and rotations projection matrix.

RECOMMENDATION:

Use the default.


CPSCF_NSEG

Controls the number of segments used to calculate the CPSCF equations.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Do not solve the CPSCF equations in segments.

$n$

User-defined. Use $n$ segments when solving the CPSCF equations.


RECOMMENDATION:

Use the default.


Example 11.254  An EDF1/6-31+G* optimization, followed by a vibrational analysis. Doing the vibrational analysis at a stationary point is necessary for the results to be valid. 

$molecule
   0  1
   O
   C  1  co
   F  2  fc  1  fco
   H  2  hc  1  hco  3  180.0

   co  =   1.2
   fc  =   1.4
   hc  =   1.0
   fco = 120.0
   hco = 120.0
$end

$rem
   JOBTYPE    opt
   METHOD     edf1
   BASIS      6-31+G*
$end

@@@

$molecule
   read
$end

$rem
   JOBTYPE    freq
   METHOD     edf1
   BASIS      6-31+G*
$end

11.10.2 Isotopic Substitutions

By default Q-Chem calculates vibrational frequencies using the atomic masses of the most abundant isotopes (taken from the Handbook of Chemistry and Physics, $63^{\ensuremath{\mathrm{rd}}}$ Edition). Masses of other isotopes can be specified using the $isotopes section and by setting the ISOTOPES $rem variable to TRUE. The format of the $isotopes section is as follows: 

$isotopes
   number_of_isotope_loops  tp_flag
   number_of_atoms  [temp pressure] (loop 1)
   atom_number1   mass1
   atom_number2   mass2
   ...
   number_of_atoms  [temp pressure] (loop 2)
   atom_number1   mass1
   atom_number2   mass2
   ...
$end

Note: Only the atoms whose masses are to be changed from the default values need to be specified. After each loop all masses are reset to the default values. Atoms are numbered according to the order in the $molecule section.

An initial loop using the default masses is always performed first. Subsequent loops use the user-specified atomic masses. Only those atoms whose masses are to be changed need to be included in the list, all other atoms will adopt the default masses. The output gives a full frequency analysis for each loop. Note that the calculation of vibrational frequencies in the additional loops only involves a rescaling of the computed Hessian, and therefore takes little additional computational time.

The first line of the $isotopes section specifies the number of substitution loops and also whether the temperature and pressure should be modified. The tp_flag setting should be set to 0 if the default temperature and pressure are to be used (298.18 K and 1 atm respectively), or else to 1 if they are to be altered. Note that the temperatures should be specified in Kelvin and pressures in atmospheres.

ISOTOPES

Specifies if non-default masses are to be used in the frequency calculation.


TYPE:

LOGICAL


DEFAULT:

FALSE


OPTIONS:

FALSE

Use default masses only.

TRUE

Read isotope masses from $isotopes section.


RECOMMENDATION:

None


Example 11.255  An EDF1/6-31+G* optimization, followed by a vibrational analysis. Doing the vibrational analysis at a stationary point is necessary for the results to be valid.

$molecule
   0  1
   C   1.08900   0.00000   0.00000
   C  -1.08900   0.00000   0.00000
   H   2.08900   0.00000   0.00000
   H  -2.08900   0.00000   0.00000
$end

$rem
   BASIS    3-21G
   JOBTYPE  opt
   METHOD   hf
$end

@@@

$molecule
   read
$end

$rem
   BASIS       3-21G
   JOBTYPE     freq
   METHOD      hf
   SCF_GUESS   read
   ISOTOPES    1
$end

$isotopes
   2   0           ! two loops, both at std temp and pressure
   4
     1   13.00336  ! All atoms are given non-default masses
     2   13.00336
     3   2.01410
     4   2.01410
   2 
     3   2.01410   ! H's replaced with D's
     4   2.01410
$end

11.10.3 Partial Hessian Vibrational Analysis

The computation of harmonic frequencies for systems with a very large number of atoms can become computationally expensive. However, in many cases only a few specific vibrational modes or vibrational modes localized in a region of the system are of interest. A typical example is the calculation of the vibrational modes of a molecule adsorbed on a surface. In such a case, only the vibrational modes of the adsorbate are useful, and the vibrational modes associated with the surface atoms are of less interest. If the vibrational modes of interest are only weakly coupled to the vibrational modes associated with the rest of the system, it can be appropriate to adopt a partial Hessian approach. In this approach,[Besley and Metcalf(2007), Besley and Bryan(2008)] only the part of the Hessian matrix comprising the second derivatives of a subset of the atoms defined by the user is computed. These atoms are defined in the $alist block. This results in a significant decrease in the cost of the calculation. Physically, this approximation corresponds to assigning an infinite mass to all the atoms excluded from the Hessian and will only yield sensible results if these atoms are not involved in the vibrational modes of interest. VPT2 and TOSH anharmonic frequencies can be computed following a partial Hessian calculation.[Hanson-Heine et al.(2012)Hanson-Heine, George, and Besley] It is also possible to include a subset of the harmonic vibrational modes with an anharmonic frequency calculation by invoking the ANHAR_SEL rem. This can be useful to reduce the computational cost of an anharmonic frequency calculation or to explore the coupling between specific vibrational modes.

Alternatively, vibrationally averaged interactions with the rest of the system can be folded into a partial Hessian calculation using vibrational subsystem analysis.[Zheng and Brooks(2005), Woodcock et al.(2008)Woodcock, Zheng, Ghysels, Shao, Kong, and Brooks] Based on an adiabatic approximation, this procedure reduces the cost of diagonalizing the full Hessian, while providing a local probe of fragments vibrations, and providing better than partial Hessian accuracy for the low frequency modes of large molecules.[Ghysels et al.(2010)Ghysels, Van Speybroeck, Pauwels, Catak, Brooks, Van Neck, and Waroquier] Mass-effects from the rest of the system can be vibrationally averaged or excluded within this scheme.

PHESS

Controls whether partial Hessian calculations are performed.


TYPE:

INTEGER


DEFAULT:

0

Full Hessian calculation


OPTIONS:

1

Partial Hessian calculation.

2

Vibrational subsystem analysis (massless).

3

Vibrational subsystem analysis (weighted).


RECOMMENDATION:

None


N_SOL

Specifies number of atoms included in the Hessian.


TYPE:

INTEGER


DEFAULT:

No default


OPTIONS:

User defined


RECOMMENDATION:

None


PH_FAST

Lowers integral cutoff in partial Hessian calculation is performed.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use default cutoffs


OPTIONS:

TRUE

Lower integral cutoffs


RECOMMENDATION:

None


ANHAR_SEL

Select a subset of normal modes for subsequent anharmonic frequency analysis.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use all normal modes


OPTIONS:

TRUE

Select subset of normal modes


RECOMMENDATION:

None


Example 11.256  This example shows an anharmonic frequency calculation for ethene where only the C-H stretching modes are included in the anharmonic analysis.

$comment
  ethene
  restricted anharmonic frequency analysis
$end

$molecule
0 1
  C   0.6665   0.0000   0.0000
  C  -0.6665   0.0000   0.0000
  H   1.2480   0.9304   0.0000
  H  -1.2480  -0.9304   0.0000
  H  -1.2480   0.9304   0.0000
  H   1.2480  -0.9304   0.0000
$end

$rem
   JOBTYPE           freq
   METHOD            hf
   BASIS             sto-3g
   ANHAR_SEL         TRUE
   N_SOL             4
$end

$alist
9
10
11
12
$end


Example 11.257  This example shows a partial Hessian frequency calculation of the vibrational frequencies of acetylene on a model of the C(100) surface

$comment
   acetylene - C(100)
   partial Hessian calculation
$end

$molecule
0 1
   C  0.000  0.659 -2.173
   C  0.000 -0.659 -2.173
   H  0.000  1.406 -2.956
   H  0.000 -1.406 -2.956
   C  0.000  0.786 -0.647
   C  0.000 -0.786 -0.647
   C  1.253  1.192  0.164
   C -1.253  1.192  0.164
   C  1.253 -1.192  0.164
   C  1.297  0.000  1.155
   C -1.253 -1.192  0.164
   C  0.000  0.000  2.023
   C -1.297  0.000  1.155
   H -2.179  0.000  1.795
   H -1.148 -2.156  0.654
   H  0.000 -0.876  2.669
   H  2.179  0.000  1.795
   H -1.148  2.156  0.654
   H -2.153 -1.211 -0.446
   H  2.153 -1.211 -0.446
   H  1.148 -2.156  0.654
   H  1.148  2.156  0.654
   H  2.153  1.211 -0.446
   H -2.153  1.211 -0.446
   H  0.000  0.876  2.669
$end

$rem
   JOBTYPE           freq
   METHOD            hf
   BASIS             sto-3g
   PHESS             TRUE
   N_SOL             4
$end

$alist
1
2
3
4
$end

11.10.4 Localized Mode Vibrational Analysis

The computation of harmonic frequencies leads to molecular vibrations described by coordinates which are often highly de-localized. For larger molecules many vibrational modes can potentially contribute to a single observed spectral band, and information about the interaction between localized chemical units can become less readily available. In certain cases, localizing vibrational modes using procedures similar to the localized orbital schemes discussed previously in this manual can therefore provide a more chemically intuitive way of analysing spectral data,[Jacob and Reiher(2009), Jacob et al.(2009a)Jacob, Luber, and Reiher, Jacob et al.(2009b)Jacob, Luber, and Reiher] interpreting two-dimensional vibrational spectra,[Hanson-Heine et al.(2016)Hanson-Heine, Husseini, Hirst, and Besley] or improving calculations that go beyond the harmonic approximation.[Cheng and Steele(2014), Panek and Jacob(2014), Hanson-Heine(2015)] It is also possible to include only a subset of the normal modes in the localization calculation by invoking the LOCALFREQ_SELECT rem variable. This can be useful to improve convergence in larger molecules or to explore the coupling between specific vibrational modes. These modes are defined in the $alist block. Alternatively it is possible to localize high and low frequency modes separately in a single calculation using LOCALFREQ_GROUPS and related inputs.

LOCAL_FREQ

Controls whether a vibrational mode localization calculation is performed.


TYPE:

INTEGER


DEFAULT:

0

Normal mode calculation.


OPTIONS:

1

Localized mode calculation with a Pipek-Mezey like criterion.

2

Localized mode calculation with a Boys like criterion.


RECOMMENDATION:

None


LOCALFREQ_THRESH

Mode localization is considered converged when the change in the localization criterion is less than $10^\ensuremath{\mathrm{}}{-LOCALFREQ\_ THRESH}$.


TYPE:

INTEGER


DEFAULT:

6


OPTIONS:

$n$

User-specified integer.


RECOMMENDATION:

None


LOCALFREQ_MAX_ITER

Controls the maximum number of mode localization sweeps permitted.


TYPE:

INTEGER


DEFAULT:

200


OPTIONS:

$n$

User-specified integer.


RECOMMENDATION:

None


LOCALFREQ_SELECT

Select a subset of normal modes for subsequent anharmonic frequency analysis.


TYPE:

LOGICAL


DEFAULT:

FALSE

Use all normal modes.


OPTIONS:

TRUE

Select a subset of normal modes.


RECOMMENDATION:

None


LOCALFREQ_GROUPS

Select the number of groups of frequencies to be localized separately within a localized mode calculation. The size of the groups are then controlled using the LOCALFREQ_GROUP1, LOCALFREQ_GROUP2, and LOCALFREQ_GROUP3 keywords.


TYPE:

INTEGER


DEFAULT:

0

Localize all normal modes together.


OPTIONS:

1

Define one subset of modes to localize independently.

2

Define two subsets of modes to localize independently.

3

Define three subsets of modes to localize independently.


RECOMMENDATION:

None


LOCALFREQ_GROUP1

Select the number of modes to include in the first subset of modes to localize independently when the keyword LOCALFREQ_GROUPS > 0.


TYPE:

INTEGER


DEFAULT:

NONE


OPTIONS:

$n$

User-specified integer.


RECOMMENDATION:

Modes will be included starting with the lowest frequency mode and then in ascending energy order up to the defined value.


LOCALFREQ_GROUP2 and LOCALFREQ_GROUP3 are defined similarly.