10.15 Indirect Nuclear Spin–Spin Coupling Constants

Indirect nuclear spin–spin coupling constants (also known as scalar couplings or 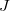$J$ -couplings) can be evaluated in Q-Chem at the Hartree–Fock and density functional levels of theory[694, 695] (restricted wave functions only). Pure and hybrid functionals are supported. To perform a 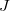$J$ -coupling calculation, set JOBTYPE to ISSC. Refer to Section 10.16.3 for more options.

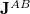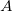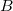The coupling tensor $\mathbf{J}^{AB}$ between atoms $A$ and $B$ is evaluated as the second derivative of the electronic energy with respect to the nuclear magnetic moments $\mathbf{m}$ ,

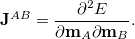$\begin{equation} \label{issc} \mathbf{J}^{AB} = \frac{\partial ^2 E}{\partial \mathbf{m}_ A \partial \mathbf{m}_ B}. \end{equation}$

(10.65)

The indirect coupling tensor has five distinct contributions. The diamagnetic spin–orbit (DSO) contribution is calculated as an expectation value with the ground state wave function. The other contributions are the paramagnetic spin–orbit (PSO), spin–dipole (SD), Fermi contact (FC), and mixed SD-FC contributions. These terms require the electronic response of the systems to the perturbation due to the magnetic nuclei. Ten distinct CPSCF equations must be solved for each perturbing nucleus, which makes the calculation of 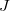$J$ -coupling constants time-consuming.

Some authors have recommended [696] calculating only the Fermi contact contribution, and skipping the other contributions for ${}^1$ H– ${}^1$ H coupling constants. For that purpose, Q-Chem allows you to skip the calculation of any of the four (FC, SD, PSO, DSO) contributions (the mixed SD-FC contributions is automatically calculated at no additional cost whenever both the SD and FC contributions are calculated). See section 10.16.3 for details. Note that omitting any of the contributions cannot be rationalized from a theoretical point of view. Results from such calculations should be interpreted extremely conservatively.

Specialized basis sets are highly recommended in any 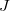$J$ -coupling calculation. The pcJ- $n$ basis set family [697] has been added to the basis set library.

Note that the Hartree–Fock level of theory is not suitable to obtain 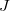$J$ -coupling constants of any degree of reliability. Instead, use GGA or hybrid density functionals.

Example 10.254 An example of 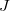$J$ -coupling calculation: Water molecule with B3LYP/cc-pVDZ

$molecule
   0 1
   O
   H1 O OH
   H2 O OH H1 HOH
   
   OH  = 0.947
   HOH = 105.5
$end

$rem
   JOBTYPE          ISSC
   EXCHANGE         B3LYP
   BASIS            cc-pVDZ
   LIN_K            FALSE
   SYMMETRY         TRUE
   MOPROP_CONV_1ST  6
$end