10.14 Linear-Scaling NMR Chemical Shifts: GIAO-HF and GIAO-DFT

The importance of nuclear magnetic resonance (NMR) spectroscopy for modern chemistry and biochemistry cannot be overestimated. Despite tremendous progress in experimental techniques, the understanding and reliable assignment of observed experimental spectra remains often a highly difficult task, so that quantum chemical methods can be extremely useful both in the solution and the solid state (e.g., Refs. Ochsenfeld:2000b,Ochsenfeld:2001,Brown:2001,Ochsenfeld:2002, Ochsenfeld:2004, and references therein).

The cost for the computation of NMR chemical shifts within even the simplest quantum chemical methods such as Hartree-Fock (HF) or density functional (DFT) approximations increases conventionally with the third power of the molecular size 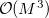$M$ , ${\cal {O}}({M^3})$ , where 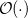${\cal {O}}({\cdot })$ stands for the scaling order. Therefore, the computation of NMR chemical shieldings has so far been limited to molecular systems in the order of 100 atoms without molecular symmetry.

For larger systems it is crucial to reduce the increase of the computational effort to linear, which has been recently achieved by Kussmann and Ochsenfeld [684, 690]. In this way, the computation of NMR chemical shifts becomes possible at both HF or DFT level for molecular systems with 1000 atoms and more, while the accuracy and reliability of traditional methods is fully preserved. In our formulation we use gauge-including atomic orbitals (GIAOs) [680, 691, 681], which have proven to be particularly successful [692]. For example, for many molecular systems the HF (GIAO-HF) approach provides typically an accuracy of 0.2–0.4 ppm for the computation of $^1$ H NMR chemical shifts (e.g. Refs. Ochsenfeld:2000b, Ochsenfeld:2001, Brown:2001, Ochsenfeld:2002,Ochsenfeld:2004).

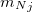NMR chemical shifts are calculated as second derivatives of the energy with respect to the external magnetic field $\ensuremath{\mathbf{B}}$ and the nuclear magnetic spin ${m_ N}_ j$ of a nucleus $N$ :

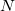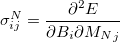$\begin{equation} \label{shift} \sigma _{ij}^ N = \frac{\partial ^2 E}{\partial B_ i \partial {M_ N}_ j} \end{equation}$

(10.64)

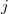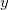where $i$ , $j$ are $x$ , $y$ , $z$ coordinates.

For the computation of the NMR shielding tensor it is necessary to solve for the response of the one-particle density matrix with respect to the magnetic field, so that the solution of the coupled perturbed SCF (CPSCF) equations either within the HF or the DFT approach is required.

These equations can be solved within a density matrix-based formalism for the first time with only linear-scaling effort for molecular systems with a non-vanishing HOMO-LUMO gap [684]. The solution is even simpler in DFT approaches without explicit exchange, since present density functionals are not dependent on the magnetic field.

The present implementation of NMR shieldings in Q-Chem employs the LinK (linear exchange K) method [264, 265] for the formation of exchange contributions [684]. Since the derivative of the density matrix with respect to the magnetic field is skew-symmetric, its Coulomb-type contractions vanish. For the remaining Coulomb-type matrices the CFMM method [693] is adapted [684]. In addition, a multitude of different approaches for the solution of the CPSCF equations can be selected within Q-Chem.

The so far largest molecular system for which NMR shieldings have been computed, contained 1003 atoms and 8593 basis functions (GIAO-HF/6-31G*) without molecular symmetry [684].