12.16 The ALMO-CIS and ALMO-CIS+CT methods
12.16.1 Theory
The ALMO-CIS [894] and ALMO-CIS+CT [895] methods are local variants of configuration interaction singles (CIS), and are formulated through the use of absolutely localized molecular orbitals (ALMOs). They share the same spirit with the TDDFT(MI) method (see Section 12.15), but were originally designed to target large numbers of excited states in atomic/molecular clusters, such as the entire  band in helium clusters that contain hundreds of atoms.
band in helium clusters that contain hundreds of atoms.
In ALMO-CIS and ALMO-CIS+CT, we solve a truncated non-orthogonal CIS eigen-equation:
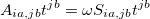 |
(12.45) |
The use of ALMOs allows associating each MO index ( ,
,  ,
, 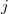 or
or 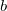 ) to a fragment. In ALMO-CIS, approximation is made such that only the amplitudes corresponding to intrafragment transitions are non-zero, i.e.,
) to a fragment. In ALMO-CIS, approximation is made such that only the amplitudes corresponding to intrafragment transitions are non-zero, i.e., 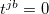 if the occupied orbital
if the occupied orbital 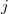 and the virtual orbital
and the virtual orbital 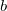 reside on two different fragments. The Hamiltonian and overlap matrix are also truncated, with
reside on two different fragments. The Hamiltonian and overlap matrix are also truncated, with  膔(
膔(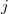 ) and
) and  膔(
膔(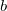 ) belonging to the same fragment. This approximation excludes interfragment charge transfer (CT) excitations entirely and sometimes may lead to insufficient accuracy. In ALMO-CIS+CT, the CT effect is reintroduced by setting a distance cutoff
) belonging to the same fragment. This approximation excludes interfragment charge transfer (CT) excitations entirely and sometimes may lead to insufficient accuracy. In ALMO-CIS+CT, the CT effect is reintroduced by setting a distance cutoff  , so that transitions between neighboring fragments within a distance smaller than
, so that transitions between neighboring fragments within a distance smaller than  are allowed (
are allowed ( 膔(
膔(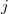 ) and
) and  膔(
膔(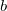 ) belonging to such a pair of fragments are also included in the eigen-equation). In both ALMO-CIS and ALMO-CIS+CT, dimension of the eigenvalue problem scales linearly with respect to system size, instead of having a quadratic scaling as in standard CIS. Because of the reduction of matrix size, it is computationally feasible to explicitly build the Hamiltonian and diagonalize it to get a full band of eigenstates for relatively large systems, and the overall scaling of ALMO-CIS/ALMO-CIS+CT is cubic, in contrast with the sixth order scaling of standard CIS for a full-spectrum calculation.
) belonging to such a pair of fragments are also included in the eigen-equation). In both ALMO-CIS and ALMO-CIS+CT, dimension of the eigenvalue problem scales linearly with respect to system size, instead of having a quadratic scaling as in standard CIS. Because of the reduction of matrix size, it is computationally feasible to explicitly build the Hamiltonian and diagonalize it to get a full band of eigenstates for relatively large systems, and the overall scaling of ALMO-CIS/ALMO-CIS+CT is cubic, in contrast with the sixth order scaling of standard CIS for a full-spectrum calculation.
Besides the full-spectrum calculations described above, use of the Davidson algorithm is also available for ALMO-CIS and ALMO-CIS+CT, which targets a few lowest excited states. This implementation, unlike the original full-spectrum version, also supports the local variants of TDDFT/TDA calculations that share the same working equation (eq. 12.45).
12.16.2 Job Control for ALMO-CIS/ALMO-CIS+CT
In addition to the standard CIS job controls variables described in Section 6.2.7, there are several additional $rem variables to specify for an ALMO-CIS/ALMO-CIS+CT calculation.
LOCAL_CIS
Invoke ALMO-CIS/ALMO-CIS+CT.
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Regular CIS
1
ALMO-CIS/ALMO-CIS+CT without RI(slow)
2
ALMO-CIS/ALMO-CIS+CT with RI
RECOMMENDATION:
2 if ALMO-CIS is desired.
NN_THRESH
The distance cutoff for neighboring fragments (between which CT is enabled).
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Do not include interfragment transitions (ALMO-CIS).

Include interfragment excitations between pairs of fragments the distances between whom
are smaller than
Bohr (ALMO-CIS+CT).
RECOMMENDATION:
None
EIGSLV_METH
Control the method for solving the ALMO-CIS eigen-equation
TYPE:
INTEGER
DEFAULT:
0
OPTIONS:
0
Explicitly build the Hamiltonian then diagonalize (full-spectrum).
1
Use the Davidson method (currently only available for restricted cases).
RECOMMENDATION:
None
Example 12.326 ALMO-CIS+CT calculation (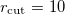 a
a ) for all the
) for all the 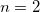 states of a helium dimer.
states of a helium dimer.
$molecule
0 1
--
0 1
He 2.8 0. 0.
--
0 1
He 0. 0. 0.
$end
$rem
basis gen
aux_basis rimp2-cc-pvdz
purecart 1111
method hf
sym_ignore true
symmetry false
frgm_method stoll
cis_n_roots 8
cis_triplets false
local_cis 2 ! use RI for ALMO-CIS
nn_thresh 10
$end
$rem_frgm
cis_n_roots 0
$end
$basis
****
HE 0
S 3 1.000000
3.84216340D+01 2.37660000D-02
5.77803000D+00 1.54679000D-01
1.24177400D+00 4.69630000D-01
S 1 1.000000
2.97964000D-01 1.00000000D+00
SP 1 1.000000
4.80000000D-02 1.00000000D+00 1.00000000D+00
****
$end