12.10 The Many-Body Expansion Method
12.10.1 Theory and Implementation Details
The many-body expansion (MBE) for a system of 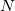 monomers is given by
monomers is given by
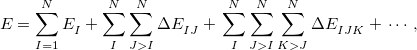 |
(12.23) |
in which 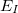 represents the energy of monomer
represents the energy of monomer 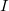 ,
, 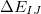 =
= 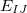

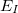

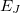 is a two-body correction for dimer
is a two-body correction for dimer 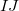 , and
, and 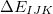 =
= 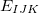

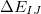

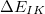

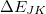

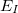

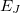

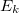 is a three-body correction for trimer
is a three-body correction for trimer 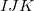 , etc. In a large system and/or a large basis set, truncation of this expression at the two- or three-body level may dramatically reduce the amount of computer time that is required to compute the energy. Convergence of the MBE can be accelerated by embedding the monomer (
, etc. In a large system and/or a large basis set, truncation of this expression at the two- or three-body level may dramatically reduce the amount of computer time that is required to compute the energy. Convergence of the MBE can be accelerated by embedding the monomer (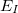 ), dimer (
), dimer (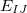 ), trimer (
), trimer (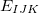 ),
),  calculations in some representation of the electrostatic potential of the rest of the system. A simple means to do this is via atom-centered point charges that could be obtained when the
calculations in some representation of the electrostatic potential of the rest of the system. A simple means to do this is via atom-centered point charges that could be obtained when the 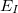 terms are calculated; this is the so-called electrostatically-embedded many-body expansion (EE-MBE) [696]. Alternatively, since the monomer electron densities are available from the
terms are calculated; this is the so-called electrostatically-embedded many-body expansion (EE-MBE) [696]. Alternatively, since the monomer electron densities are available from the 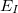 terms as well, one could use these densities to compute the actual monomer–monomer Coulomb interactions, and this forms the basis of the fragment molecular orbital (FMO) method [697, 698]. Note that Q-Chem’s present implementation of Eq. eq:mb is very preliminary. In particular, the “bodies” (fragments) cannot be covalently bonded to one another, and therefore this is a method appropriate for non-covalent clusters of molecules. Moreover, individual subsystem calculations have not yet been parallelized across processors, hence the present implementation is not using the real power of the MBE. While significant speed-ups may be observed at the two-body level, three-body (and higher) calculations are presently useful only as proof-of-concept exercises, as the total wall time will often be larger than the corresponding supersystem calculation. Analytic gradients are not yet available. These deficiencies will be rectified in a future release of the program.
terms as well, one could use these densities to compute the actual monomer–monomer Coulomb interactions, and this forms the basis of the fragment molecular orbital (FMO) method [697, 698]. Note that Q-Chem’s present implementation of Eq. eq:mb is very preliminary. In particular, the “bodies” (fragments) cannot be covalently bonded to one another, and therefore this is a method appropriate for non-covalent clusters of molecules. Moreover, individual subsystem calculations have not yet been parallelized across processors, hence the present implementation is not using the real power of the MBE. While significant speed-ups may be observed at the two-body level, three-body (and higher) calculations are presently useful only as proof-of-concept exercises, as the total wall time will often be larger than the corresponding supersystem calculation. Analytic gradients are not yet available. These deficiencies will be rectified in a future release of the program.
It is well known that the interaction energies of non-covalent clusters are usually overestimated (often substantially) owing to basis-set superposition error (BSSE), which disappears only very slowly as the basis sets approach completeness. The widely used Boys–Bernardi counterpoise (CP) procedure corrects for this by computing all energies (including cluster and monomers) using the cluster basis set. (Note, however, that basis-set extrapolation is still necessary for high-quality binding energies; in 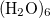 , for example, a CP-corrected MP2/aug-cc-pVQZ calculation is still
, for example, a CP-corrected MP2/aug-cc-pVQZ calculation is still 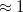 kcal/mol from the MP2 basis-set limit [717]. Fortunately, the MBE allows for use of large basis sets in order to perform basis-set extrapolations in sizable clusters [717, 718].) Two low-cost CP corrections that are consistent with an
kcal/mol from the MP2 basis-set limit [717]. Fortunately, the MBE allows for use of large basis sets in order to perform basis-set extrapolations in sizable clusters [717, 718].) Two low-cost CP corrections that are consistent with an  -body expansion have been proposed: the many-body CP correction, MBCP(
-body expansion have been proposed: the many-body CP correction, MBCP( ) [717, 718], and the
) [717, 718], and the  -body Valiron-Mayer function counterpoise correction, VMFC(
-body Valiron-Mayer function counterpoise correction, VMFC( ) [719]. The two approaches are equivalent for
) [719]. The two approaches are equivalent for 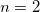 but the MBCP(
but the MBCP( ) method requires far fewer subsystem calculations starting at
) method requires far fewer subsystem calculations starting at 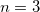 and is thus significantly cheaper, while affording very similar results as compared to VMFC(
and is thus significantly cheaper, while affording very similar results as compared to VMFC( ) [717, 718].
) [717, 718].
Q-Chem’s implementation of the EE-MBE( ) approach (electrostatically-embedded
) approach (electrostatically-embedded  -body expansion) is designed to use self-consistent charges generated by XPol calculations. As such, a MBE calculation is requested by setting both MANY_BODY_INT and XPOL = TRUE. The variable MBE_ORDER sets the truncation order,
-body expansion) is designed to use self-consistent charges generated by XPol calculations. As such, a MBE calculation is requested by setting both MANY_BODY_INT and XPOL = TRUE. The variable MBE_ORDER sets the truncation order,  . If one wishes to use MBE(
. If one wishes to use MBE( ) without charge embedding, then XPOL must still be set to TRUE but XPOL_MPOL_ORDER should be set to GAS. For EE-MBE(
) without charge embedding, then XPOL must still be set to TRUE but XPOL_MPOL_ORDER should be set to GAS. For EE-MBE( ), the user has the choice of Mulliken, Löwdin, or CHELPG (specified using XPOL_CHARGE_TYPE), and these charges can either be evaluated self-consistently or fixed at the outset. (In the latter case, they are gas-phase charges computed at the geometry that each monomer has in the cluster environment. As an alternative to point charges, density embedding is also available, in which Coulomb interactions are computed between proper monomer electron densities. The MBE with density embedding is equivalent to the original version of the fragment molecular orbital (FMO) [697]. (Many subsequent modifications to the FMO algorithm have been introduced [698, 720] but are not yet available in Q-Chem. These include, in particular, the option to use point charges or approximate electron repulsion integrals to compute the Coulomb interactions between distant monomers [721, 722], which actually makes FMO more like EE-MBE at long range.) This density-embedded version of FMO is available in Q-Chem by setting XPOL_MPOL_ORDER = DENSITY.
), the user has the choice of Mulliken, Löwdin, or CHELPG (specified using XPOL_CHARGE_TYPE), and these charges can either be evaluated self-consistently or fixed at the outset. (In the latter case, they are gas-phase charges computed at the geometry that each monomer has in the cluster environment. As an alternative to point charges, density embedding is also available, in which Coulomb interactions are computed between proper monomer electron densities. The MBE with density embedding is equivalent to the original version of the fragment molecular orbital (FMO) [697]. (Many subsequent modifications to the FMO algorithm have been introduced [698, 720] but are not yet available in Q-Chem. These include, in particular, the option to use point charges or approximate electron repulsion integrals to compute the Coulomb interactions between distant monomers [721, 722], which actually makes FMO more like EE-MBE at long range.) This density-embedded version of FMO is available in Q-Chem by setting XPOL_MPOL_ORDER = DENSITY.
Researchers who use Q-Chem’s MBE code are asked to cite Ref. Richard:2014 and—if the MBCP( ) method is used—to cite Ref. Richard:2013a as well.
) method is used—to cite Ref. Richard:2013a as well.
12.10.2 Job Control and Examples for Many-Body Calculations
The following $rem variables control MBE jobs.
MANY_BODY_INT
Perform a MBE calculation.
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Perform a MBE calculation.
FALSE
Do not perform a MBE calculation.
RECOMMENDATION:
NONE
MBE_ORDER
Controls the truncation order
for MBE.
TYPE:
INTEGER
DEFAULT:
2
OPTIONS:
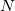
Order of MBE
RECOMMENDATION:
EE-MBE and FMO can be performed up to fifth and third order, respectively.
XPOL_FIX_MULLIKEN
Control to use self-consistent charge for EE-MBE.
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Perform an EE-MBE without self-consistent charge.
FALSE
Perform an EE-MBE with self-consistent charge.
RECOMMENDATION:
The charges are derived from isolated monomers without self-consistent process. It is available to use with Mulliken charges, Löwdin charges and CHELPG charges
XPOL_FIX_TIP3P
Use charges corresponding to TIP3P water for EE-MBE.
TYPE:
BOOLEAN
DEFAULT:
FALSE
OPTIONS:
TRUE
Perform an EE-MBE with charges corresponding to TIP3P water.
FALSE
Do not perform an EE-MBE with charges corresponding to TIP3P water.
RECOMMENDATION:
Only available for water molecules
MANY_BODY_BSSE
Controls the type of many-body BSSE corrections.
TYPE:
STRING
DEFAULT:
MBCP
OPTIONS:
MBCP
Use many-body counterpoise correction.
VMFC
Use Valiron-Mayer function counterpoise correction.
RECOMMENDATION:
NONE.
MBE_BSSE_ORDER
Controls the order of many-body BSSE corrections.
TYPE:
INTEGER
DEFAULT:
2
OPTIONS:

Order of many-body BSSE corrections
RECOMMENDATION:
MBCP and VMFC can be performed up to third and fourth order, respectively.
Example 12.279 Example showing a 3-body EE-MBE calculation using self-consistent CHELPG charges.
$rem
sym_ignore true
method rimp2
basis cc-pvdz
aux_basis rimp2-cc-pvdz
n_frozen_core fc
xpol true
xpol_mpol_order charges
xpol_charge_type qchelpg
many_body_int true
mbe_order 3
purecart 1111
scf_convergence 7
thresh 14
$end
$molecule
0 1
--
0 1
O -1.126149 -1.748387 -0.423240
H -0.234788 -1.493897 -0.661862
H -1.062789 -2.681331 -0.218819
--
0 1
O -0.254210 1.611495 -1.293845
H -1.001520 1.163510 -1.690129
H -0.153399 2.411746 -1.809248
--
0 1
O 1.694541 -0.226287 1.705739
H 0.785920 0.073487 1.677909
H 2.047134 0.150917 2.511706
--
0 1
O -0.864533 0.522472 1.218817
H -0.694120 1.093542 0.469789
H -1.131418 -0.310426 0.829702
$end
Example 12.280 Example showing a 3-body MBCP calculation.
$rem
sym_ignore true
method b3lyp
basis sto-3g
xpol true
xpol_mpol_order gas
many_body_bsse mbcp
mbe_bsse_order 3
purecart 1111
scf_convergence 7
thresh 14
$end
$molecule
0 1
--
0 1
O -1.126149 -1.748387 -0.423240
H -0.234788 -1.493897 -0.661862
H -1.062789 -2.681331 -0.218819
--
0 1
O -0.254210 1.611495 -1.293845
H -1.001520 1.163510 -1.690129
H -0.153399 2.411746 -1.809248
--
0 1
O 1.694541 -0.226287 1.705739
H 0.785920 0.073487 1.677909
H 2.047134 0.150917 2.511706
--
0 1
O -0.864533 0.522472 1.218817
H -0.694120 1.093542 0.469789
H -1.131418 -0.310426 0.829702
$end