B.6 Fundamental ERI

The fundamental ERI and the basis of all ERI algorithms is usually represented[Gill(1994)]

	$\displaystyle [\ensuremath{\mathbf{0}}]^{(0)}$	$\displaystyle \! \! \! =\! \! \!$	$\displaystyle [ss\vert ss]^{(0)}$		(B.3)
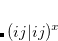	$\displaystyle$	$\displaystyle \! \! \! =\! \! \!$	$\displaystyle D_ A D_ B D_ C D_ D \int {e^{-\alpha \left\| {{\rm {\bf r}}_{\rm {\bf 1}} -{\rm {\bf A}}} \right\|^2}e^{-\beta \left\| {{\rm {\bf r}}_{\rm {\bf 1}} -{\rm {\bf B}}} \right\|^2}\left[ {\frac{1}{r_{12} }} \right]e^{-\gamma \left\| {{\rm {\bf r}}_{\rm {\bf 2}} -{\rm {\bf C}}} \right\|^2}e^{-\delta \left\| {{\rm {\bf r}}_2 -{\rm {\bf D}}} \right\|^2}d{\rm {\bf r}}_{\rm {\bf 1}} d{\rm {\bf r}}_{\rm {\bf 2}} }$		(B.4)

which can be reduced to a one-dimensional integral of the form

$\begin{equation} \label{eq:b4} [{\rm {\bf 0}}]^{(0)}=U(2\, {\vartheta }^2)^{1/2} \left({\frac{2}{\pi }}\right)^{1/2} \, \int \limits _0^1 {e^{-Tu^2}du} \end{equation}$

(B.5)

and can be efficiently computed using a modified Chebyshev interpolation scheme.[Gill et al.(1991)Gill, Johnson, and Pople] Equation eq:b4 can also be adapted for the general case $[\ensuremath{\mathbf{0}}]^{(m)}$ integrals required for most calculations. Following the fundamental ERI, building up to the full bra-ket ERI (or intermediary matrix elements, see later) are the problems of angular momentum and contraction.

Note: Square brackets denote primitive integrals and parentheses denote fully-contracted integrals.