9.6 Forces and Vibrational Frequencies with ECPs

It is important to be able to optimize geometries using pseudopotentials and for this purpose Q-Chem contains analytical first derivatives of the nuclear potential energy term for ECPs.

The ECP package is also integrated with the vibrational analysis package and it is therefore possible to compute the vibrational frequencies (and hence the infrared and Raman spectra) of systems in which some of the atoms may bear ECPs.

Q-Chem cannot calculate analytic second derivatives of the nuclear potential-energy term when ECPs are used, and must therefore resort to finite difference methods. However, for HF and DFT calculations, it can compute analytic second derivatives for all other terms in the Hamiltonian. The program takes full advantage of this by only computing the potential-energy derivatives numerically, and adding these to the analytically calculated second derivatives of the remaining energy terms.

There is a significant speed advantage associated with this approach as, at each finite-difference step, only the potential-energy term needs to be calculated. This term requires only three-center integrals, which are far fewer in number and much cheaper to evaluate than the four-center, two-electron integrals associated with the electron-electron interaction terms. Readers are referred to Table 10.1 for a full list of the analytic derivative capabilities of Q-Chem.

Example 9.209 Structure and vibrational frequencies of TeO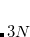 $_{2}$ using Hartree-Fock theory and the Stuttgart relativistic large-core ECPs. Note that the vibrational frequency job reads both the optimized structure and the molecular orbitals from the geometry optimization job that precedes it. Note also that only the second derivatives of the potential energy term will be calculated by finite difference, all other terms will be calculated analytically.

$molecule
   0  1
   Te
   O1  Te  r
   O2  Te  r  O1  a

   r = 1.8
   a = 108
$end

$rem
   JOBTYPE    opt
   METHOD     hf
   ECP        srlc
$end

@@@

$molecule
   read
$end

$rem
   JOBTYPE     freq
   METHOD      hf
   ECP         srlc
   SCF_GUESS   read
$end