B.8 Contraction Problem

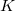The contraction problem may be described by considering a general contracted ERI of $s$ -type functions derived from the STO-3G basis set. Each basis function has degree of contraction $K$ = 3. Thus, the ERI may be written

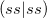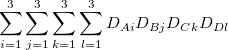$\displaystyle (ss\vert ss)$	$\displaystyle =$	$\displaystyle \sum \limits _{i=1}^3 {\sum \limits _{j=1}^3 {\sum \limits _{k=1}^3 {\sum \limits _{l=1}^3 {D_{Ai} D_{Bj} D_{Ck} D_{Dl}} } } } \nonumber$
$\displaystyle$	$\displaystyle$	$\displaystyle \times \int {e^{-\alpha _ i \left\| {{\rm {\bf r}}_{\rm {\bf 1}} -{\rm {\bf A}}} \right\|^2}e^{-\beta _ j \left\| {{\rm {\bf r}}_{\rm {\bf 1}} -{\rm {\bf B}}} \right\|^2}\left[ {\frac{1}{r_{12} }} \right]e^{-\gamma _ k \left\| {{\rm {\bf r}}_{\rm {\bf 2}} -{\rm {\bf C}}} \right\|^2}e^{-\delta _ l \left\| {{\rm {\bf r}}_2 -{\rm {\bf D}}} \right\|^2}d{\rm {\bf r}}_{\rm {\bf 1}} d{\rm {\bf r}}_{\rm {\bf 2}} } \nonumber$
$\displaystyle$	$\displaystyle =$	$\displaystyle \sum \limits _{i=1}^3 {\sum \limits _{j=1}^3 {\sum \limits _{k=1}^3 {\sum \limits _{l=1}^3 {[s_ i s_ j \vert s_ k s_ l ]} } } }$	(B.5)

and requires 81 primitive integrals for the single ERI. The problem escalates dramatically for more highly contracted sets (STO-6G, 6-311G) and has been the motivation for the development of techniques for shell-pair modeling [758], in which a second shell-pair is constructed with fewer primitives that the first, but introduces no extra error relative to the integral threshold sought.

The Pople-Hehre axis-switch method [750] is excellent for high contraction low angular momentum integral classes.