B.5 Shell-Quartets and Integral Classes
Given a sorted list of shell-pair data, it is possible to construct all potentially important shell-quartets by pairing of the shell-pairs with one another. Because the shell-pairs have been sorted, it is possible to deal with batches of integrals of the same type or class (e.g., 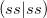 ,
, 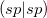 ,
, 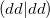 , etc.) where an integral class is characterized by both angular momentum (
, etc.) where an integral class is characterized by both angular momentum (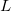 ) and degree of contraction (
) and degree of contraction (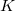 ). Such an approach is advantageous for vector processors and for semi-direct integral algorithms where the most expensive (high
). Such an approach is advantageous for vector processors and for semi-direct integral algorithms where the most expensive (high 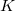 or
or 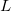 integral classes can be computed once, stored in memory (or disk) and only less expensive classes rebuilt on each iteration.
integral classes can be computed once, stored in memory (or disk) and only less expensive classes rebuilt on each iteration.
While the shell-pairs may have been carefully screened, it is possible for a pair of significant shell-pairs to form a shell-quartet which need not be computed directly. Three cases are:
The quartet is equivalent, by point group symmetry, to another quartet already treated.
The quartet can be ignored on the basis of cheaply computed ERI bounds [744] on the largest quartet bra-ket.
On the basis of an incremental Fock matrix build, the largest density matrix element which will multiply any of the bra-kets associated with the quartet may be negligibly small.
Note: Significance and negligibility is always based on the level of integral threshold set by the $rem variable THRESH.