12.5 Energy Decomposition and Charge-Transfer Analysis
12.5.1 Energy Decomposition Analysis
The strength of intermolecular binding is inextricably connected to the fundamental nature of interactions between the molecules. Intermolecular complexes can be stabilized through weak dispersive forces, electrostatic effects (e.g., charge–charge, charge–dipole, and charge–induced dipole interactions) and donor-acceptor type orbital interactions such as forward and back-donation of electron density between the molecules. Depending on the extent of these interactions, the intermolecular binding could vary in strength from just several kJ/mol (van der Waals complexes) to several hundred kJ/mol (metal–ligand bonds in metal complexes). Understanding the contributions of various interaction modes enables one to tune the strength of the intermolecular binding to the ideal range by designing materials that promote desirable effects. One of the most powerful techniques that modern first principles electronic structure methods provide to study and analyze the nature of intermolecular interactions is the decomposition of the total molecular binding energy into the physically meaningful components such as dispersion, electrostatic, polarization, charge transfer, and geometry relaxation terms.
Energy decomposition analysis based on absolutely-localized molecular orbitals (ALMO EDA) is implemented in Q-Chem [685], including the open shell generalization [684]. In ALMO EDA, the total intermolecular binding energy is decomposed into the “frozen density” component (FRZ), the polarization (POL) term, and the charge-transfer (CT) term. The “frozen density” term is defined as the energy change that corresponds to bringing infinitely separated fragments together without any relaxation of their MOs. The FRZ term is calculated as a difference between the FRAGMO guess energy and the sum of the converged SCF energies on isolated fragments. The polarization (POL) energy term is defined as the energy lowering due to the intrafragment relaxation of the frozen occupied MOs on the fragments. The POL term is calculated as a difference between the converged SCF MI energy and the FRAGMO guess energy. Finally, the charge-transfer (CT) energy term is due to further interfragment relaxation of the MOs. It is calculated as a difference between the fully converged SCF energy and the converged SCF MI energy.
The total charge-transfer term includes the energy lowering due to electron transfer from the occupied orbitals on one molecule (more precisely, occupied in the converged SCF MI state) to the virtual orbitals of another molecule as well as the further energy change caused by induction that accompanies such an occupied/virtual mixing. The energy lowering of the occupied-virtual electron transfer can be described with a single non-iterative Roothaan-step correction starting from the converged SCF MI solution. Most importantly, the mathematical form of the SCF MI(RS) energy expression allows one to decompose the occupied-virtual mixing term into bonding and back-bonding components for each pair of molecules in the complex. The remaining charge-transfer energy term (i.e., the difference between SCF MI(RS) energy and the full SCF energy) includes all induction effects that accompany occupied-virtual charge transfer and is generally small. This last term is called higher order (HO) relaxation. Unlike the RS contribution, the higher order term cannot be divided naturally into forward and back-donation terms. The BSSE associated with each charge-transfer term (forward donation, back-bonding, and higher order effects) can be corrected individually.
To perform energy decomposition analysis, specify fragments in the $molecule section and set JOBTYPE to EDA. For a complete EDA job, Q-Chem
performs the SCF on isolated fragments (use the $rem_frgm section if convergence issues arise but make sure that keywords in this section do not affect the final energies of the fragments),
generates the FRAGMO guess to obtain the FRZ term,
converges the SCF MI equations to evaluate the POL term,
performs evaluation of the perturbative (RS or ARS) variational correction to calculate the forward donation and back-bonding components of the CT term for each pair of molecules in the system,
converges the full SCF procedure to evaluate the higher order relaxation component of the CT term.
The FRGM_LPCORR keyword controls evaluation of the CT term in an EDA job. To evaluate all of the CT components mentioned above set this keyword to RS_EXACT_SCF or ARS_EXACT_SCF. If the HO term in not important then the final step (i.e., the SCF calculation) can be skipped by setting FRGM_LPCORR to RS or ARS. If only the total CT term is required then set FRGM_LPCORR to EXACT_SCF.
ALMO charge transfer analysis (ALMO CTA) is performed together with ALMO EDA [686]. The ALMO charge transfer scale,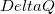 
, provides a measure of the distortion of the electronic clouds upon formation of an intermolecular bond and is such that all CT terms (i.e., forward-donation, back-donation, and higher order relaxation) have well defined energetic effects (i.e., ALMO CTA is consistent with ALMO EDA).
To remove the BSSE from the CT term (both on the energy and charge scales), set EDA_BSSE to TRUE. Q-Chem generates an input file for each fragment with MIXED basis set to perform the BSSE correction. As with all jobs with MIXED basis set and d or higher angular momentum basis functions on atoms, the PURECART keyword needs to be initiated. If EDA_BSSE=TRUE GENERAL basis sets cannot be used in the current implementation.
Please note that the energy of the geometric distortion of the fragments is not included into the total binding energy calculated in an EDA job. The geometry optimization of isolated fragments must be performed to account for this term.
Example 12.269 Energy decomposition analysis of the binding energy between the water molecules in a tetramer. ALMO CTA results are also printed out.
$molecule
0 1
--
0 1
O -0.106357 0.087598 0.127176
H 0.851108 0.072355 0.136719
H -0.337031 1.005310 0.106947
--
0 1
O 2.701100 -0.077292 -0.273980
H 3.278147 -0.563291 0.297560
H 2.693451 -0.568936 -1.095771
--
0 1
O 2.271787 -1.668771 -2.587410
H 1.328156 -1.800266 -2.490761
H 2.384794 -1.339543 -3.467573
--
0 1
O -0.518887 -1.685783 -2.053795
H -0.969013 -2.442055 -1.705471
H -0.524180 -1.044938 -1.342263
$end
$rem
JOBTYPE EDA
METHOD EDF1
BASIS 6-31(+,+)g(d,p)
PURECART 1112
FRGM_METHOD GIA
FRGM_LPCORR RS_EXACT_SCF
EDA_BSSE TRUE
$end
Example 12.270 An open shell EDA example of Na
interacting with the methyl radical.
$molecule
1 2
--
0 2
C -1.447596 -0.000023 0.000019
H -1.562749 0.330361 -1.023835
H -1.561982 0.721445 0.798205
H -1.561187 -1.052067 0.225866
--
1 1
Na 1.215591 0.000036 -0.000032
$end
$rem
JOBTYPE EDA
METHOD B3LYP
BASIS 6-31G*
UNRESTRICTED TRUE
SCF_GUESS FRAGMO
FRGM_METHOD STOLL
FRGM_LPCORR RS_EXACT_SCF
EDA_BSSE TRUE
DIIS_SEPARATE_ERRVEC 1
$end
12.5.2 Analysis of Charge-Transfer Based on Complementary Occupied/Virtual Pairs
In addition to quantifying the amount and energetics of intermolecular charge transfer, it is often useful to have a simple description of orbital interactions in intermolecular complexes. The polarized ALMOs obtained from the SCF MI procedure and used as a reference basis set in the decomposition analysis do not directly show which occupied-virtual orbital pairs are of most importance in forming intermolecular bonds. By performing rotations of the polarized ALMOs within a molecule, it is possible to find a "chemist’s basis set” that represents bonding between molecules in terms of just a few localized orbitals called complementary occupied-virtual pairs (COVPs). This orbital interaction model validates existing conceptual descriptions of intermolecular bonding. For example, in the modified ALMO basis, hydrogen bonding in water dimer is represented as an electron pair localized on an oxygen atom donating electrons to the O–H 
-antibonding orbital on the other molecule [687], and the description of synergic bonding in metal complexes agrees well with simple Dewar-Chatt-Duncanson model [703, 686, 704].
Set EDA_COVP to TRUE to perform the COVP analysis of the CT term in an EDA job. COVP analysis is currently implemented only for systems of two fragments. Set EDA_PRINT_COVP to TRUE to print out localized orbitals that form occupied-virtual pairs. In this case, MOs obtained in the end of the run (SCF MI orbitals, SCF MI(RA) orbitals, converged SCF orbitals) are replaced by the orbitals of COVPs. Each orbital is printed with the corresponding CT energy term in kJ/mol (instead of the energy eigenvalues in hartrees). These energy labels make it easy to find correspondence between an occupied orbital on one molecule and the virtual orbital on the other molecule. The examples below show how to print COVP orbitals. One way is to set $rem variable PRINT_ORBITALS, the other is to set IANLTY to 200 and use the $plots section in the Q-Chem input. In the first case the orbitals can be visualized using MOLDEN (set MOLDEN_FORMAT to TRUE), in the second case use VMD or a similar third party program capable of making 3D plots.
Example 12.271 COVP analysis of the CT term. The COVP orbitals are printed in the Q-Chem and MOLDEN formats.
$molecule
0 1
--
0 1
O -1.521720 0.129941 0.000000
H -1.924536 -0.737533 0.000000
H -0.571766 -0.039961 0.000000
--
0 1
O 1.362840 -0.099704 0.000000
H 1.727645 0.357101 -0.759281
H 1.727645 0.357101 0.759281
$end
$rem
JOBTYPE EDA
BASIS 6-31G
PURECART 1112
METHOD B3LYP
FRGM_METHOD GIA
FRGM_LPCORR RS_EXACT_SCF
EDA_COVP TRUE
EDA_PRINT_COVP TRUE
PRINT_ORBITALS 16
MOLDEN_FORMAT TRUE
$end
Example 12.272 COVP analysis of the CT term. Note that it is not necessary to run a full EDA job. It is suffice to set FRGM_LPCORR to RS or ARS and EDA_COVP to TRUE to perform the COVP analysis. The orbitals of the most significant occupied-virtual pair are printed into an ASCII file called plot.mo which can be converted into a cube file and visualized in VMD.
$molecule
0 1
--
0 1
O -1.521720 0.129941 0.000000
H -1.924536 -0.737533 0.000000
H -0.571766 -0.039961 0.000000
--
0 1
O 1.362840 -0.099704 0.000000
H 1.727645 0.357101 -0.759281
H 1.727645 0.357101 0.759281
$end
$rem
JOBTYPE SP
BASIS 6-31G
PURECART 1112
METHOD B3LYP
FRGM_METHOD GIA
FRGM_LPCORR RS
IANLTY 200
EDA_COVP TRUE
EDA_PRINT_COVP TRUE
$end
$plots
MOs
80 -4.0 4.0
60 -3.0 3.0
60 -3.0 3.0
2 0 0 0
6 11
$end