5.10 Frozen Natural Orbitals in CCD, CCSD, OD, QCCD, and QCISD Calculations

Large computational savings are possible if the virtual space is truncated using the frozen natural orbital (FNO) approach. For example, using a fraction 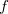$f$ of the full virtual space results in a 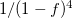$1/(1-f)^4$ -fold speed up for each CCSD iteration (CCSD scales with the forth power of the virtual space size). FNO-based truncation for ground-states CC methods was introduced by Bartlett and co-workers [275, 276, 277]. Extension of the FNO approach to ionized states within EOM-CC formalism was recently introduced and benchmarked [278] (see Section 6.7.7).

The FNOs are computed as the eigenstates of the virtual-virtual block of the MP2 density matrix [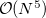 ${\cal {O}}({N^5})$ scaling], and the eigenvalues are the occupation numbers associated with the respective FNOs. By using a user-specified threshold, the FNOs with the smallest occupations are frozen in CC calculations. This could be done in CCSD, CCSD(T), CCSD(2), CCSD(dT), CCSD(fT) as well as CCD, OD,QCCD, VQCCD, and all possible triples corrections for these wavefunctions.

The truncation can be performed using two different schemes. The first approach is to simply specify the total number of virtual orbitals to retain, e.g., as the percentage of total virtual orbitals, as was done in Refs. Taube:2005,Taube:2008. The second approach is to specify the percentage of total natural occupation (in the virtual space) that needs to be recovered in the truncated space. These two criteria are referred to as the POVO (percentage of virtual orbitals) and OCCT (occupation threshold) cutoffs, respectively [278].

Since the OCCT criterion is based on the correlation in a specific molecule, it yields more consistent results than POVO. For ionization energy calculations employing 99–99.5% natural occupation threshold should yields errors (relative to the full virtual space values) below 1 kcal/mol [278]. The errors decrease linearly as a function of the total natural occupation recovered, which can be exploited by extrapolating truncated calculations to the full virtual space values. This extrapolation scheme is called the extrapolated FNO (XFNO) procedure [278]. The linear behavior is exhibited by the total energies of the ground and the ionized states as a function of OCCT. Therefore, the XFNO scheme can be employed even when the two states are not calculated on the same level, e.g., in adiabatic energy differences and EOM-IP-CC(2,3) calculations (more on this in Ref. Landau:2010).

The FNO truncation often causes slower convergence of the CCSD and EOM procedures. Nevertheless, despite larger number of iterations, the FNO-based truncation of orbital space reduces computational cost considerably, with a negligible decline in accuracy [278].

5.10.1 Job Control Options

CC_FNO_THRESH

Initialize the FNO truncation and sets the threshold to be used for both cutoffs (OCCT and POVO)

TYPE:

INTEGER

DEFAULT:

None

OPTIONS:

range

0000-10000

$abcd$

Corresponding to $ab.cd$ %

RECOMMENDATION:

None

CC_FNO_USEPOP

Selection of the truncation scheme

TYPE:

INTEGER

DEFAULT:

1

OCCT

OPTIONS:

0

POVO

RECOMMENDATION:

None

5.10.2 Example

Example 5.100 CCSD(T) calculation using FNO with POVO=65%

$molecule
  0 1
  O
  H 1 1.0
  H 1 1.0 2 100.
$end

$rem
  method = CCSD(T)
  basis = 6-311+G(2df,2pd)
  CC_fno_thresh 6500       65% of the virtual space
  CC_fno_usepop 0 
$end