Q-Chem 5.0 User’s Manual

10.7 Spin and Charge Densities at the Nuclei

Gaussian basis sets violate nuclear cusp conditions [626, 627, 628]. This may lead to large errors in wave function at nuclei, particularly for spin density calculations [629]. This problem can be alleviated by using an averaging operator that compute wave function density based on constraints that wave function must satisfy near Coulomb singularity [630, 631]. The derivation of operators is based on hyper virial theorem [632] and presented in Ref. Rassolov:1996b. Application to molecular spin densities for spin-polarized [631] and DFT [633] wave functions show considerable improvement over traditional delta function operator.

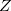One of the simplest forms of such operators is based on the Gaussian weight function $\exp [-(Z/r_{0})^{2}(\ensuremath{\mathbf{r}}-\ensuremath{\mathbf{R}})^{2}]$ that samples the vicinity of a nucleus of charge $Z$ located at 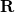$\bf R$. The parameter 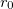$r_0$ has to be small enough to neglect two-electron contributions of the order 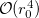$\mbox{${\cal {O}}({r_{0}^4})$}$ but large enough for meaningful averaging. The range of values between 0.15–0.3 a.u. has been shown to be adequate, with final answer being relatively insensitive to the exact choice of 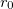$r_0$ [630, 631]. The value of 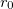$r_0$ is chosen by RC_R0 keyword in the units of 0.001 a.u. The averaging operators are implemented for single determinant Hartree-Fock and DFT, and correlated SSG wave functions. Spin and charge densities are printed for all nuclei in a molecule, including ghost atoms.

RC_R0

Determines the parameter in the Gaussian weight function used to smooth the density at the nuclei.


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Corresponds the traditional delta function spin and charge densities

$n$

corresponding to $n\times 10^{-3}$ a.u.


RECOMMENDATION:

We recommend value of 250 for a typical spit valence basis. For basis sets with increased flexibility in the nuclear vicinity the smaller values of $r_0$ also yield adequate spin density.