8.2 ECP Reconstruction

The ECP matrix elements are arguably the most difficult one-electron integrals in existence. Indeed, using current methods, the time taken to compute the ECP integrals can exceed the time taken to compute the far more numerous electron repulsion integrals. Q-Chem 5.0 implements a state-of-the-art ECP method [532] based on efficient recursion relations and upper bounds. This method relies on a restricted radial potential 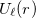$U_\ell (r)$ , where the radial power is only ever zero, i.e. 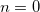$n=0$ . 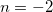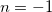Whilst true for some ECPs, such as the Stuttgart-Bonn sets, many other ECPs have radial potentials containing $n= -2$ and $n=-1$ terms. To overcome this challenge, we reconstruct these ECP radial potentials using only 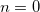$n=0$ terms. 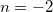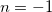Each $n=-2$ and $n=-1$ term is expanded as a sum of three 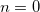$n=0$ terms, each with independent contraction coefficient 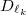$D_{\ell _ k}$ and Gaussian exponent 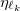$\eta _{\ell _ k}$ . The Gaussian exponents are given by a predetermined recipe and the contraction coefficients are computed in a least squares fitting procedure. The errors introduced by the ECP reconstruction are insignificant and of the same order as those introduced by numerical integration present in other ECP methods. This reconstruction is carried out automatically by Q-Chem at run time.