Q-Chem 5.0 User’s Manual

10.4 Orbital Localization

The concept of localized orbitals has already been visited in this manual in the context of perfect-pairing and methods. As the SCF energy is independent of the partitioning of the electron density into orbitals, there is considerable flexibility as to how this may be done. The canonical picture, where the orbitals are eigenfunctions of the Fock operator is useful in determining reactivity, for, through Koopmans’ theorem, the orbital energy eigenvalues give information about the corresponding ionization energies and electron affinities. As a consequence, the HOMO and LUMO are very informative as to the reactive sites of a molecule. 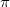In addition, in small molecules, the canonical orbitals lead us to the chemical description of $\sigma $ and $\pi $ bonds.

In large molecules, however, the canonical orbitals are often very delocalized, and so information about chemical bonding is not readily available from them. Here, orbital localization techniques can be of great value in visualizing the bonding, as localized orbitals often correspond to the chemically intuitive orbitals which might be expected.

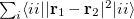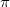Q-Chem has three post-SCF localization methods available. These can be performed separately over both occupied and virtual spaces. The localization scheme attributed to Boys [612, 613] minimizes the radial extent of the localized orbitals, i.e., $\sum _ i \langle ii| |{\bf r}_1-{\bf r}_2|^2 |ii\rangle $, and although is relatively fast, does not separate $\sigma $ and $\pi $ orbitals, leading to two ‘banana-orbitals’ in the case of a double bond [614]. Pipek-Mezey localized orbitals [614] maximize the locality of Mulliken populations, and are of a similar cost to Boys localized orbitals, but maintain $\sigma -\pi $ separation. Edmiston-Ruedenberg localized orbitals [615] maximize the self-repulsion of the orbitals, 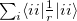$\sum _ i \langle ii|\frac{1}{r}|ii\rangle $. This is more computationally expensive to calculate as it requires a two-electron property to be evaluated, but the work of Dr. Joe Subotnik [616] and later Prof. Young-Min Rhee and Westin Kurlancheek with Prof. Martin Head-Gordon at Berkeley has, through use of the Resolution of the Identity approximation, reduced the formal cost may be asymptotically reduced to cubic scaling with the number of occupied orbitals.

BOYSCALC

Specifies the Boys localized orbitals are to be calculated


TYPE:

INTEGER


DEFAULT:

0


OPTIONS:

0

Do not perform localize the occupied space.

1

Allow core-valence mixing in Boys localization.

2

Localize core and valence separately.


RECOMMENDATION:

None


ERCALC

Specifies the Edmiston-Ruedenberg localized orbitals are to be calculated


TYPE:

INTEGER


DEFAULT:

06000


OPTIONS:

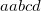
$aabcd$

 

$aa$

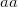
specifies the convergence threshold.
 

If $aa>3$, the threshold is set to $10^{-aa}$. The default is 6.
 

If $aa=1$, the calculation is aborted after the guess, allowing Pipek-Mezey
 

orbitals to be extracted.

$b$

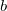
specifies the guess:
 

0 Boys localized orbitals. This is the default
 

1 Pipek-Mezey localized orbitals.

$c$

specifies restart options (if restarting from an ER calculation):
 

0 No restart. This is the default
 

1 Read in MOs from last ER calculation.
 

2 Read in MOs and RI integrals from last ER calculation.

$d$

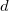
specifies how to treat core orbitals

 

0 Do not perform ER localization. This is the default.
 

1 Localize core and valence together.
 

2 Do separate localizations on core and valence.
 

3 Localize only the valence electrons.

 

4 Use the $localize section.


RECOMMENDATION:

ERCALC 1 will usually suffice, which uses threshold $10^{-6}$.


The $localize section may be used to specify orbitals subject to ER localization if require. It contains a list of the orbitals to include in the localization. These may span multiple lines. If the user wishes to specify separate beta orbitals to localize, include a zero before listing the beta orbitals, which acts as a separator, e.g., 

$localize
2 3 4 0  
2 3 4 5 6 
$end