4.10 Hartree-Fock and Density-Functional Perturbative Corrections

4.10.1 Theory

Closely related to the dual-basis approach of Section 4.9, but somewhat more general, is the Hartree-Fock perturbative correction (HFPC) developed by Deng et al. [294, 295]. An HFPC calculation consists of an iterative HF calculation in a small primary basis followed by a single Fock matrix formation, diagonalization, and energy evaluation in a larger, secondary basis. In the following, we denote a conventional HF calculation by HF/basis, and a HFPC calculation by HFPC/primary/secondary. 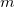Using a primary basis of $n$ functions, the restricted HF matrix elements for a 2 $m$ -electron system are

$\begin{equation} F_{\mu \nu } = h_{\mu \nu } + \sum _{\lambda \sigma }^{n} P_{\lambda \sigma } \left[(\mu \nu |\lambda \sigma ) - \frac{1}{2}(\mu \lambda |\nu \sigma )\right] \end{equation}$

(4.105)

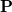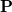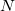Solving the Roothaan-Hall equation in the primary basis results in molecular orbitals and an associated density matrix, $\ensuremath{\mathbf{P}}$ . In an HFPC calculation, $\ensuremath{\mathbf{P}}$ is subsequently used to build a new Fock matrix, $\ensuremath{\mathbf{F}}^{[1]}$ , in a larger secondary basis of $N$ functions

$\begin{equation} F_{ab}^{[1]} = h_{ab} + \sum _{\lambda \sigma }^{n} P_{\lambda \sigma } \left[(ab|\lambda \sigma ) - \frac{1}{2}(a\lambda |b\sigma )\right] \label{eq:F1} \end{equation}$

(4.106)

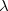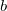where $\lambda$ , $\sigma$ indicate primary basis functions and $a$ , $b$ represent secondary basis functions. Diagonalization of $\ensuremath{\mathbf{F}}^{[1]}$ affords improved molecular orbitals and an associated density matrix $\ensuremath{\mathbf{P}}^{[1]}$ . The HFPC energy is given by

$\begin{equation} \label{eq:EHFPC} E^\text {HFPC} = \sum _{ab}^ N P^{[1]}_{ab} h_{ab} + \frac{1}{2} \sum _{abcd}^{N} P^{[1]}_{ab}P^{[1]}_{cd} \bigl [2(ab|cd) - (ac|bd)\bigr ] \end{equation}$

(4.107)

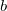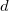where $a$ , $b$ , $c$ and $d$ represent secondary basis functions. This differs from the DBHF energy evaluation where $\ensuremath{\mathbf{PP}}^{[1]}$ , rather than $\ensuremath{\mathbf{P}}^{[1]}\ensuremath{\mathbf{P}}^{[1]}$ , is used. The inclusion of contributions that are quadratic in $\ensuremath{\mathbf{PP}}^{[1]}$ is the key reason for the fact that HFPC is more accurate than DBHF.

Unlike dual-basis HF, HFPC does not require that the small basis be a proper subset of the large basis, and is therefore able to jump between any two basis sets. Benchmark study of HFPC on a large and diverse data set of total and reaction energies demonstrate that, for a range of primary/secondary basis set combinations, the HFPC scheme can reduce the error of the primary calculation by around two orders of magnitude at a cost of about one third that of the full secondary calculation [294, 295].

A density-functional version of HFPC (“DFPC”) [296] seeks to combine the low cost of pure DFT calculations using small bases and grids, with the high accuracy of hybrid calculations using large bases and grids. The DFPC approach is motivated by the dual-functional method of Nakajima and Hirao [297] and the dual-grid scheme of Tozer et al. [298] Combining these features affords a triple perturbation: to the functional, to the grid, and to the basis set. We call this approach density-functional “triple jumping”.

4.10.2 Job Control

HFPC/DFPC calculations are controlled with the following $rem. HFPT turns on the HFPC/DFPC approximation. Note that HFPT_BASIS specifies the secondary basis set.

HFPT

Activates HFPC/DFPC calculation.

TYPE:

LOGICAL

DEFAULT:

FALSE

OPTIONS:

Single-point energy only

RECOMMENDATION:

Use Dual-Basis to capture large-basis effects at smaller basis cost. See reference for recommended basis set, functional, and grid pairings.

HFPT_BASIS

Specifies the secondary basis in a HFPC/DFPC calculation.

TYPE:

STRING

DEFAULT:

None

OPTIONS:

None

RECOMMENDATION:

See reference for recommended basis set, functional, and grid pairings.

DFPT_XC_GRID

Specifies the secondary grid in a HFPC/DFPC calculation.

TYPE:

STRING

DEFAULT:

None

OPTIONS:

None

RECOMMENDATION:

See reference for recommended basis set, functional, and grid pairings.

DFPT_EXCHANGE

Specifies the secondary functional in a HFPC/DFPC calculation.

TYPE:

STRING

DEFAULT:

None

OPTIONS:

None

RECOMMENDATION:

See reference for recommended basis set, functional, and grid pairings.

4.10.3 Examples

Example 4.67 Input for a HFPC single-point calculation.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE      sp
   EXCHANGE     hf
   BASIS        cc-pVDZ  ! primary basis
   HFPT_BASIS   cc-pVQZ  ! secondary basis
   PURECART     1111     ! set to purecart of the target basis 
   HFPT         true
$end

Example 4.68 Input for a DFPC single-point calculation.

$molecule
   0 1
   H
   H   1   0.75
$end

$rem
   JOBTYPE          sp
   EXCHANGE         blyp               ! primary functional
   DFPT_EXCHANGE    b3lyp              ! secondary functional
   DFPT_XC_GRID     00075000302        ! secondary grid
   XC_GRID          0                  ! primary grid
   HFPT_BASIS       6-311++G(3df,3pd)  ! secondary basis
   BASIS            6-311G*            ! primary basis
   PURECART         1111
   HFPT             true
$end