6.11 Real-Time SCF Methods (RT-TDDFT, RT-HF, OSCF2)

Linear response calculations are the most efficient way to predict resonant electronic response frequencies and intensities. Q-Chem can also propagate mean-field theories (HF, DFT) in real-time with and without dissipation and finite-temperature effects. These methods time-evolve the Liouville-von Neumann equation of motion for a one-particle density operator, 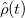$\hat{\rho }(t)$ :

$\begin{equation} \label{eq:LvN} \begin{array}{r} (i/\hbar ) \hat{\rho }(t) = \bigl [\hat{F}\{ \rho \} ,\hat{\rho }(t)\bigr ] \end{array} \end{equation}$

(6.88)

These real-time methods are useful for simulating attosecond to picosecond timescales, density response to multiple or strong applied fields, and timescales of energy relaxation. Symmetry, non-singlet densities, Meta-GGAs and 5th-rung functionals are not supported for real-time propagation, and nuclei are fixed. The CPU cost of a single time step is comparable to that of a single SCF cycle, if the modified-midpoint unitary transformation (MMUT) propagation algorithm [511] is employed, and no more than a few times the cost of a single SCF cycle if predictor/corrector algorithms (which facilitate stable time propagation using much larger time steps) are used [512]. Memory costs are similar to those of a ground-state SCF calculation, which for large systems, or those with a large density of states, represents a dramatic reduction in the memory requirement relative to linear-reponse TDDFT. The number of required Fock-build steps can be estimated from the default electronic time-step, which is 0.02 atomic units (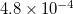 $4.8 \times 10^{-4}$ fs). The real-time code exploits real-time shared-memory parallelism, and the use of 8 or more cores (–nt 8) is suggested. The input file of a basic real-time propagation is relatively simple, but sophisticated jobs require additional input files, and generate additional output.

Example 6.194 Q-Chem Basic RT-TDDFT job for BH3.

$molecule
   0 1
   B    0.000000     0.000000     0.000000
   H    1.115609    -0.322048     0.260309
   H   -0.332368     1.137184     0.111382
   H   -0.782205    -0.814474    -0.375294
$end

$rem
   SCF_GUESS         core
   GEN_SCFMAN        true 
   RTTDDFT           1 
   BASIS             3-21g
   THRESH            10 
   SCF_CONVERGENCE   9 
   EXCHANGE          b3lyp
   SYMMETRY          false
   SYM_IGNORE        TRUE
   SCF_ALGORITHM     DIIS
   UNRESTRICTED      FALSE
   MAX_SCF_CYCLES    200
$end

Before executing this job, a directory (/logs) must be made in the output directory of the job to collect most of the results of the propagation. By default, a real-time job begins from the ground state SCF density, applies a weak, brief (0.07 atomic time units) oscillating electric field to the $y$ -axis of a molecule which excites a superposition of all $y$ -polarized excited states, and outputs the resulting time-dependent dipole moment, energy and other quantities to the logs directory. The parameters of the time-dependent run are printed when the propagation begins. During the propagation the state of the molecule and propagation is summarized in the Q-Chem output file, including estimates of the elapsed and remaining simulation wall-time. Propagation stops when MaxIter time steps are exceeded, or will stop prematurely if the density matrix becomes nonphysical. The logs directory will be populated by several text, white space delimited tables by default. 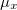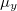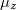The ./logs/Pol.csv file is a table consisting of time (in a.u.), $\mu _ x$ , $\mu _ y$ , $\mu _ z$ , total energy, 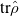$\mbox{tr}\hat{\rho }$ , the gap, the electronic energy, and two unused columns. The ./logs/Fourier_x.csv file contains Fourier transform $\mathcal{F}[\mu _ x(t)]$ , in the format of its total value in energy units (eV) followed by its negative imaginary part and then its real part. Analogous files ./logs/Fourier_y.csv and ./logs/Fourier_z.csv are also created.

By adjusting the options of the propagation with a file TDSCF.prm, a much larger amount of output can be generated, including the electron and hole densities at all times as sequential MolDen files (*.mol) viewable with the free package Gabedit (gabedit.sourceforge.net). The *.mol files generated by the real-time code have fractional orbital occupation numbers, and do not render properly in viewers other than Gabedit to our knowledge. So long as the applied field is weak and has short duration the positions at which peaks appear in the Fourier are the same as a linear-response TDDFT-RPA job (note: not the same as a LR-TDDFT-TDA job), as shown in the sample. In an energy-conserving job, the width of the peak is inversely proportional to the duration of the signal sample used to construct the Fourier transform. If the applied field pulse is long (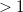 $> 1$ a.u.), or has strong intensity ( 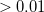$>0.01$ a.u.) non-linear response can be studied. Non-linear effects in real-time SCF are an area of active investigation and development.

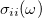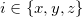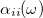The absorption cross-section $\sigma _{ii}(\omega )$ in the $i$ direction, $i\in \{ x,y,z\}$ , can be obtained from the imaginary part of the frequency-dependent polarizability $\alpha _{ii}(\omega )$ :

$\begin{equation} \sigma _{ii}(\omega ) = \left(\frac{4\pi \omega }{c}\right) \Im \bigl [\alpha _{ii}(\omega )\bigr ] \; , \end{equation}$

(6.89)

and the rotationally-averaged absorption spectrum (within the dipole approximation) is

$\begin{equation} \label{eq:RT-TDDFT_ spectrum} A(\omega ) = \tfrac {1}{3}\bigl [\sigma _{xx}(\omega ) + \sigma _{yy}(\omega ) + \sigma _{zz}(\omega )\bigr ] \; . \end{equation}$

(6.90)

The frequency-dependent polarizability 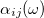$\alpha _{ij}(\omega )$ is obtained from the Fourier transform of 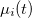$\mu _ i(t)$ , for a perturbing field in the 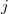$j$ direction [512]:

$\begin{equation} \alpha _{ij}(\omega ) = \frac{ \mathcal{F}\bigl [\mu _ i(t)\bigr ] }{ \mathcal{F}\bigl [E_ j(t)\bigr ] } \; . \end{equation}$

(6.91)

Thus to compute the spectrum in Eq. eq:RT-TDDFT_spectrum, three RT-TDDFT simulations are required, perturbing separately in the 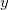$x$ , $y$ , and $z$ directions.

Because of the large number of floating point arguments used to control a real-time job, a separate input file TDSCF.prm in the same directory as the Q-Chem input file is used for parameters. The file is two columns of plain text. The first column is a string naming the parameter (which must match the case and spelling printed in the output exactly to be interpreted correctly), and the second column is a floating point number. The number must only be followed by a new line. Several inputs are interpreted as true = 1 or false = 0. The most useful parameters are discussed in this section. The code will signal if this file is not found and default values will be supplied instead.

Example 6.195 Q-Chem Typical TDSCF.prm for a real-time B3LYP calculation.

dt  0.02
Stabilize  0
TCLOn 0
MaxIter  80000
ApplyImpulse  1
ApplyCw  0
FieldFreq 0.7 
Tau 0.07
FieldAmplitude 0.001
ExDir 1.0
EyDir 1.0
EzDir 1.0
Print 0
StatusEvery 10
SaveDipoles  1
DipolesEvery 2
SavePopulations  0
SaveFockEnergies  0
WriteDensities  0
SaveEvery 500
FourierEvery 5000
MMUT 1
LFLPPC 0

Parameter String	Explanation
`dt`	timestep (atomic units) > 0.02 may be unstable.
`Stabilize`	$>0$ Forces positive occupation numbers.
`MaxIter`	Maximum Timesteps
`ApplyImpulse`	0 = No applied gaussian impulse
`ApplyCw`	0 = No Continuous Wave, 1 = Cosine applied field.
`FieldFreq`	Frequency of applied field (atomic units)
`Tau`	Time-variance of Gaussian Impulse (atomic units)
`FieldAmplitude`	Max. amplitude of field (atomic units)
`ExDir`	Field Polarization Vector (x-component)
`EyDir`	Field Polarization Vector (y-component)
`EzDir`	Field Polarization Vector (z-component)
`Print`	Value $>0$ makes print more debug output.
`StatusEvery`	Iterations between status in output file
`SaveDipoles`	0 = No Pol.csv generated.
`DipolesEvery`	Iterations between samples of Dipole
`SavePopulations`	1 = Saves diagonal of the density
`SaveFockEnergies`	1 = Saves diagonal of the Fock matrix
`WriteDensities`	$>0$ generates .mol files readable with Gabedit
`SaveEvery`	Iterations between writing of all files in /logs
`FourierEvery`	Iterations between Fourier Transform
`FourierZoom`	A zoom parameter which controls resolution of FT.
`MMUT`	Modified midpoint unitary transform propagator calculation (default) [511]
`LFLPPC`	Predictor-corrector propagator [512]

Table 6.4: TDSCF.prm Parameters

Any undocumented options not discussed above are not officially supported at this time.